Презентация на тему: Решение уравнений с квадратным корнем

Свободный член положительный. Если свободный член приведенного уравнения положителен, то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента. Если q > 0 и р > 0 , то оба корня отрицательны. Если q > 0 и р < 0 , то оба корня положительные. Пример 1 х2 + 10х + 9 = 0, х1 = - 1 и х2 = - 9, т.к. q = 9 > 0 и р = 10 > 0; Пример 2 х2 – 6х + 9 = 0, х1 = 3 и х2 = 3, т.к. q = 9 > 0 и р = - 6 < 0. Назад

Свободный член отрицательный. Если свободный член приведенного уравнения отрицателен, то уравнение имеет два различных по знаку корня. Если q < 0 и р > 0 , то больший по модулю корень будет отрицателен. Если q < 0 и р < 0, то больший по модулю корень будет положителен. Пример 1 х2 + 2х – 8 = 0, х1 = - 4 и х2 = 2, т.к. q = - 8 < 0 и р = 2 > 0 ; Пример 2 х2 – 2х – 15 = 0, х1 = 5 и х2 = - 3, т.к. q = - 15 < 0 и р = - 2 < 0. Назад

Решение уравнений с использованием теоремы Виета Приведенное квадратное уравнение имеет вид х2 + рх + q = 0. Его корни удовлетворяют теореме Виета: х1 · х2 = q х1 + х2 = - р. По коэффициентам можно предсказать знаки корней: Свободный член «+» Свободный член «-» Назад

Способы решений полных квадратных уравнений. Разложение Выделение Теорема Виета «Переброска» Свойство коэффициентов Графическое решение Выйти С помощью Дискриминанта

Свойства коэффициентов квадратного уравнения. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Первое свойство Второе свойство Третье свойство Назад

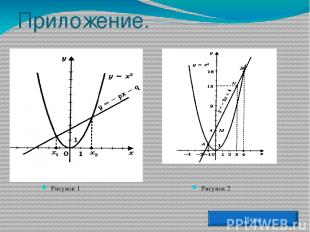
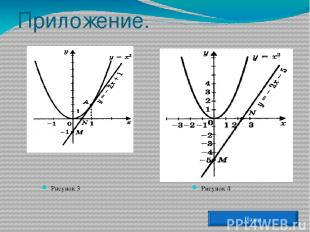
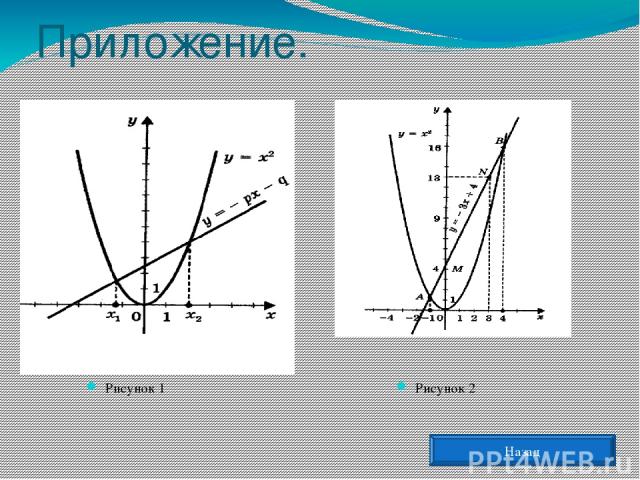
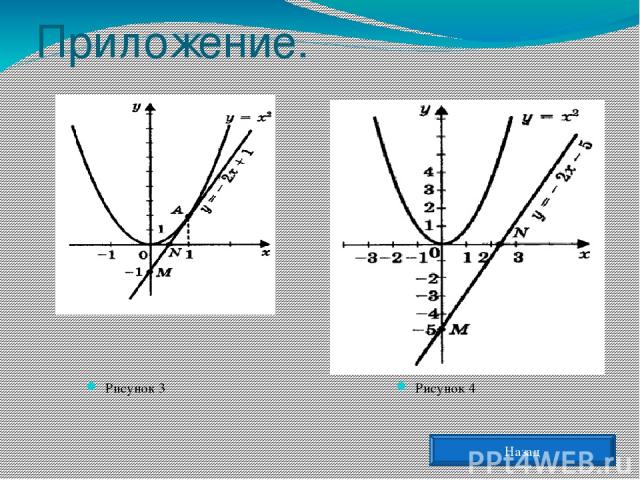
Графическое решение квадратных уравнений. Преобразуем уравнение х2 + рх + q = 0 и получим вид: х2 = - рх - q . Построим графики зависимостей у = х2 и у = - рх - q . График первой зависимости - парабола, проходящая через начало координат. График второй зависимости – прямая . (приложение 1, рис.1). Возможны следующие случаи: прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; прямая и парабола могут касаться и имеют одну общую точку, значит уравнение имеет одно решение; прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней. Назад Примеры

С помощью Дискриминанта. Дискриминант позволяет определить сколько же корней имеет данное квадратное уравнение. Формула корней квадратного уравнения имеет вид: она позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Таким образом, квадратное уравнение ах2 + bх + с = 0 , если D > 0, то имеет два различных корня; если D = 0, то имеет единственный корень; если D < 0, то не имеет корней. Назад

Решение уравнения способом «переброски». Умножая обе части квадратного уравнения на а, получаем уравнение а 2 х2 + аb х + а с = 0. Пусть а х = у, откуда ; тогда получим уравнение у2 + bу + а с = 0, равносильное данному. С помощью теоремы Виета найдем корни: у1 и у2, где у1 у2 = ас и у1 + у2 = - b. Окончательно получаем и . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. Пример 2х2 – 11х + 15 = 0, «перебросим» коэффициент 2 к свободному члену: у2 – 11у + 30 = 0, согласно теореме Виета найдем корни: у1у2 = 30 и у1 + у2 = 11, у1 = 5 и у2 = 6, окончательно получим: х1 = 5/2 и х2 = 6/2, х1 = 2,5 и х2 = 3. Ответ: 2,5 и 3. Назад

Спасибо за внимание!