Презентация на тему: Решение систем способом подстановки

Тема: «Решение систем, содержащих уравнение второй степени способом подстановки». 900igr.net

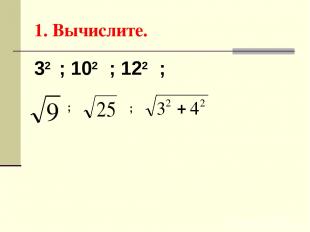
1. Вычислите. 32 ; 102 ; 122 ; ; ;

2. Назовите 3 решения уравнения: а) х – у = 1; в) 6 + 0х = 2у; б) ху = 0; г) 0х + 0у = 0.

3. Выразите переменную х через у: а) у + х = 5; г) ху = 2; б) у – х = 17; д) х – 3у =0. в) 2х – 10у = 2;

4. Представьте в виде многочлена: а) (3 + у)2 ; б) (а – 2)2

5. Являются ли решением системы х + у = 4, ху = 3; Пары чисел (2;2) ; (3;1); (6;-2).

5. Решите систему уравнений: х + у = 2, х2 + у2 = 2.

Алгоритм решения системы уравнений способом подстановки. Выразить одну переменную через другую из одного уравнения системы; Подставить полученное выражение в другое уравнение системы вместо этой переменной; Решить полученное уравнение с одной переменной; Найти значения соответствующие второй переменной.

х2 + у2 = 41, х2 + у2 = 41, х2 + (1 + х)2=41, у – х = 1; у = 1 + х; у = 1 + х; х2+ 1 + 2х + х2- 41= 0, 2х2 + 2х – 40 = 0, у = 1 + х; у = 1 + х; х2 + х – 20 = 0, у = 1 + х; Решим первое уравнение системы: х2 + х – 20 = 0, Х1= Х2= Подставим эти значения во второе уравнение системы: х1= 4, х2= -5, у1 = 1 +4 = 5, у2= 1 + (-5) = -4. Ответ: (4; 5); (-5; -4). х= 10 – 3у, х = 10 – 3у, х = 10 – 3у, ху = 3; (10 – 3у)у = 3; 10у – 3у2 - 3 = 0; Решим второе уравнение системы: -3у2 +10у – 3 = 0, 3у2 - 10у + 3 = 0, У1 = у2 = ; Подставим эти значения в первое уравнение системы: х1= 10 – 3 3=1, х2= 10 – 3 = 9, у1= 3, у2= ⅓ Ответ: (1; 3); (9; ⅓).

Подберите второе уравнение так, чтобы оба уравнения составляли систему: у = х + 2, … .