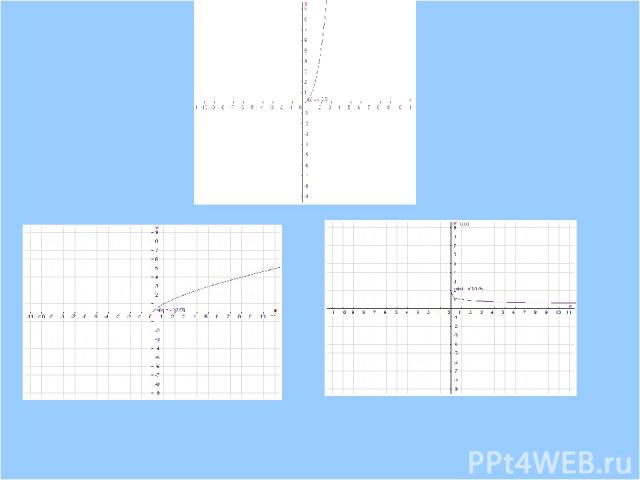
Презентация на тему: Свойства и график степенной функции

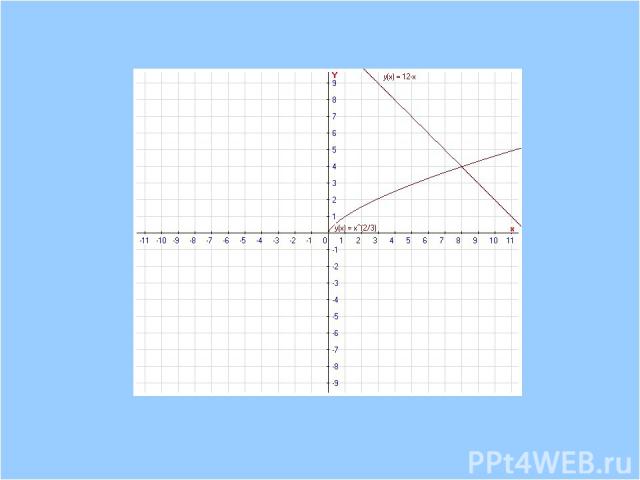
1)Имеет ли смысл выражение: а)4-1/2;б)(-8)1/3;в)0,032/7;г)0-1/8; 2)Вычислите: а)85/3; б) в)(1/625)-1/4; 3)Решите уравнение: а) х3=8; б) х4=-16; в) х6-7=0;г) х3=2-х; д) =1; е) х2/3=1; ж) х2/3=12-х; 900igr.net

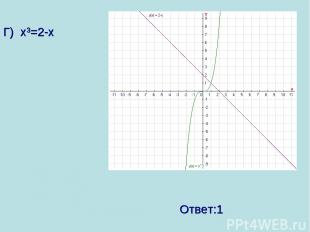
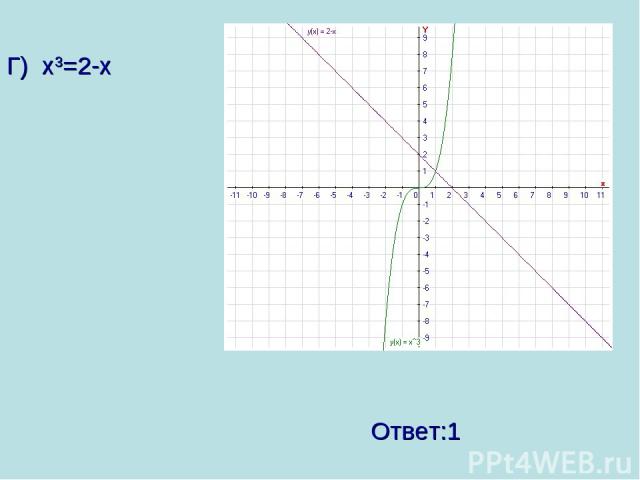
Г) х3=2-х Ответ:1

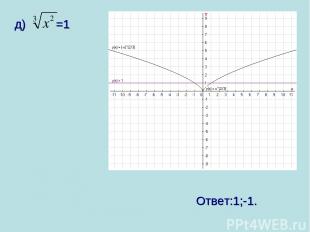
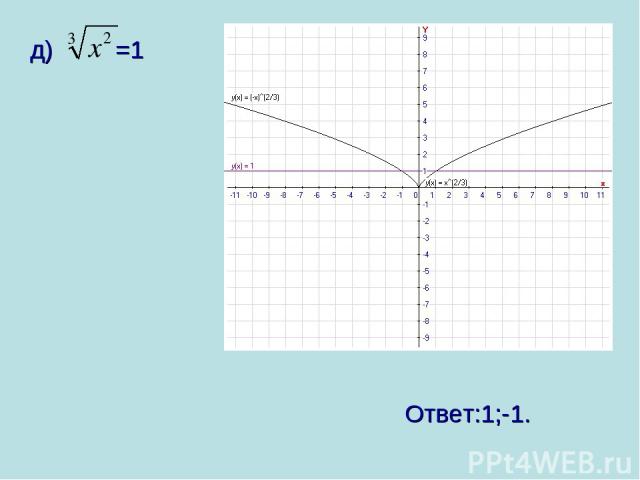
д) =1 Ответ:1;-1.

Степенные функции, их свойства и графики.

Определение: Функции вида y=xr, где r-любое действительное число называют степенными функциями.

Вид графика степенной функции зависит от знака и чётности/нечётности показателя степени. Рассмотрим степенные функции с целым показателем и выделить их общие свойства и различия

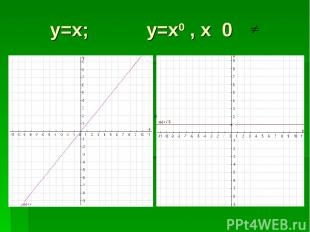
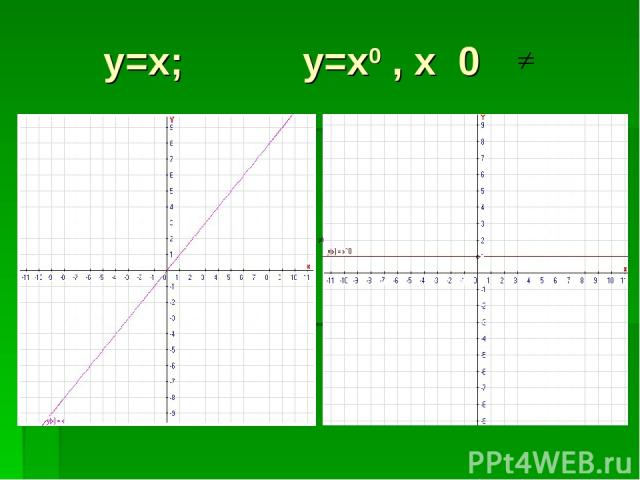
y=x; y=x0 , x 0

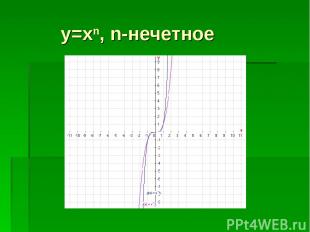
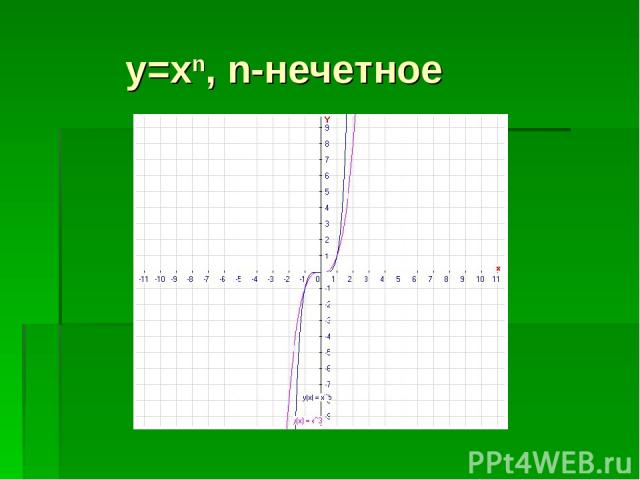
y=xn, n-нечетное

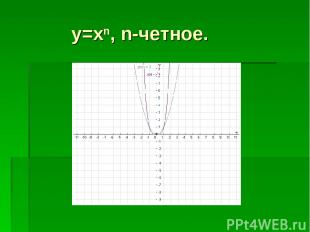
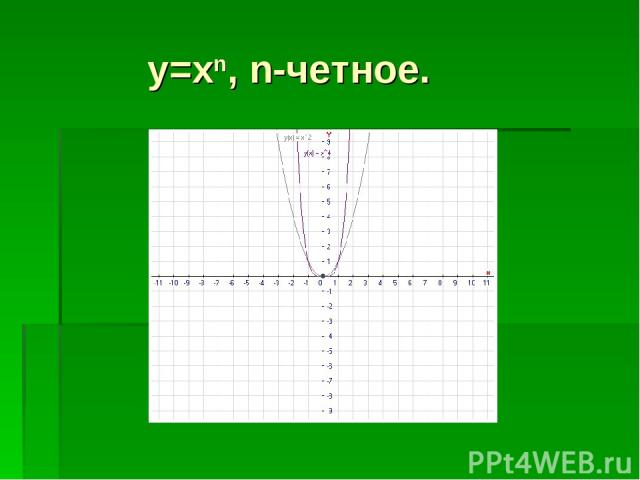
y=xn, n-четное.

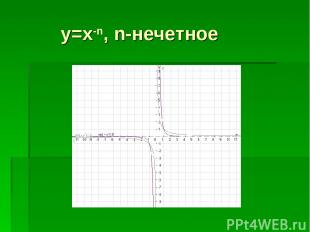
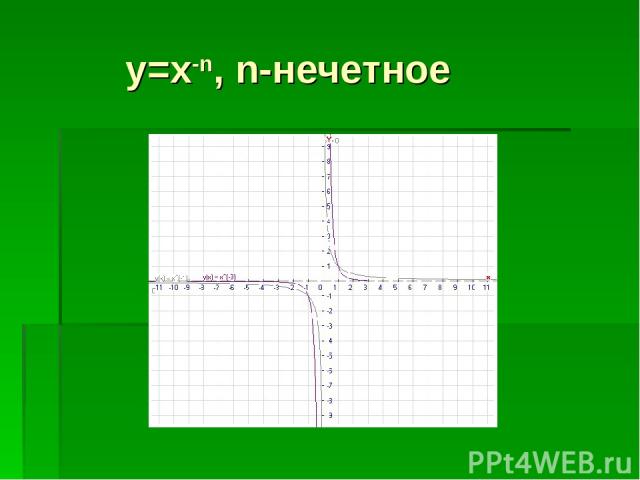
y=x-n, n-нечетное

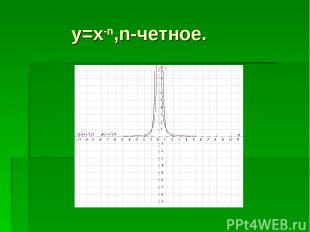
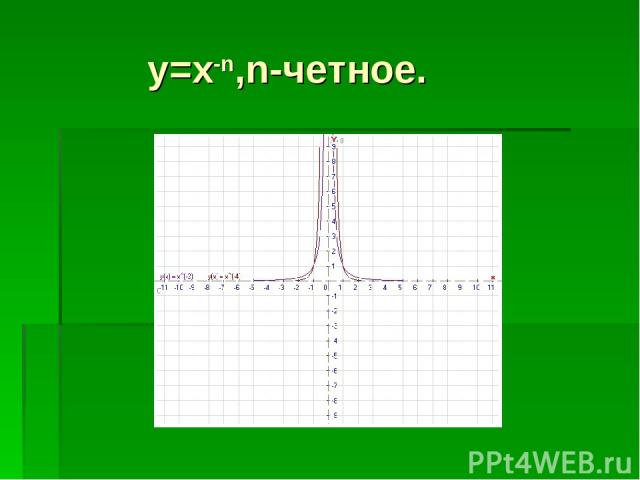
y=x-n,n-четное.

Вывод Анализ графиков степенной функции показал, что функция y=xn, где n принадлежит N, определена при всех действительных значениях x, а функция y=x-n определена при х не равном 0.

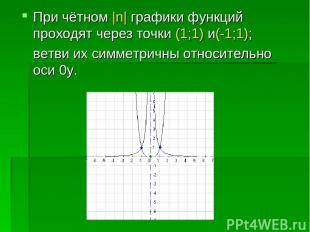
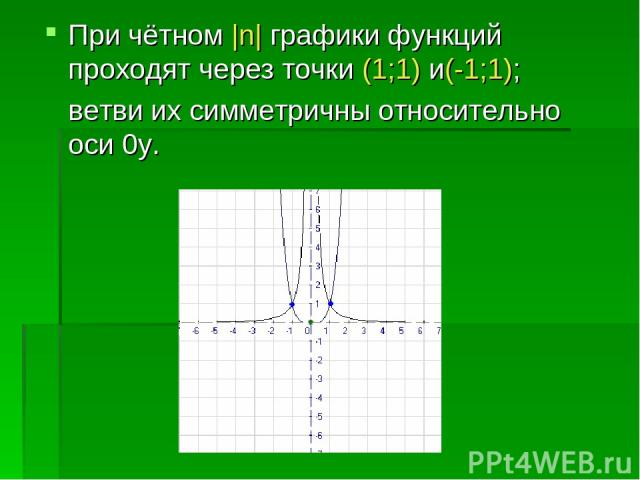
При чётном |n| графики функций проходят через точки (1;1) и(-1;1); ветви их симметричны относительно оси 0y.

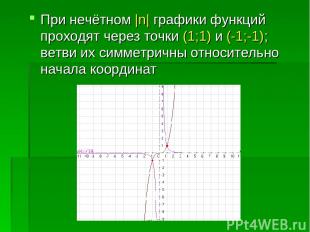
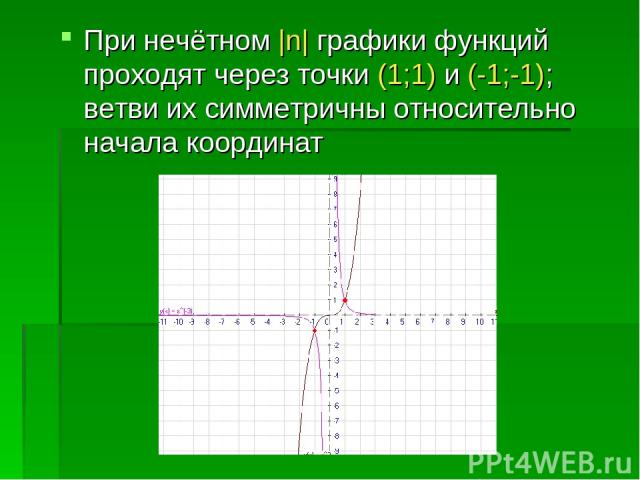
При нечётном |n| графики функций проходят через точки (1;1) и (-1;-1); ветви их симметричны относительно начала координат

Степенные функции, их свойства и графики.

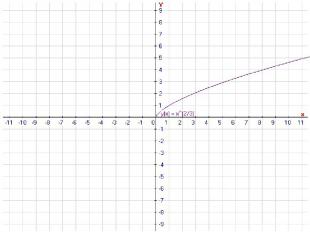
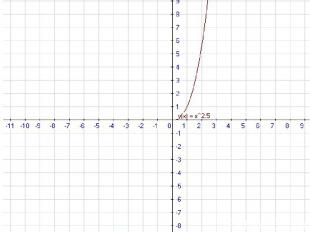
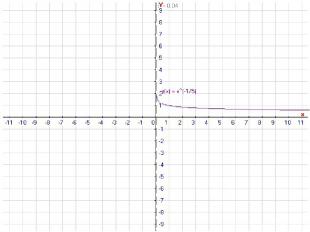
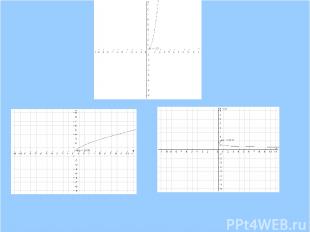
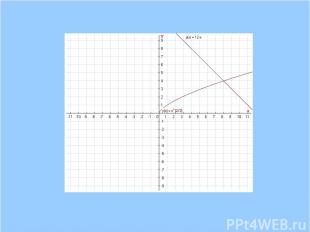
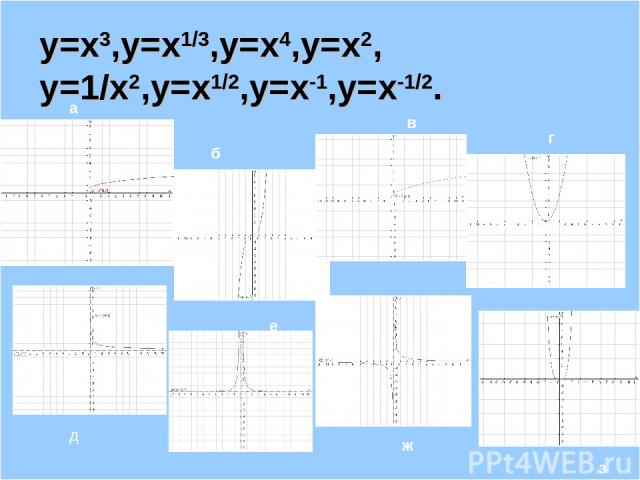
y=x3,y=x1/3,y=x4,y=x2, y=1/x2,y=x1/2,y=x-1,y=x-1/2. a а г г д е ж з б в д ж з

2)Укажите область определения степенной функции y=xr, если показатель степени r принимает значения: а) n; б)-n; в) 1/n,n N. 3)Найдите область значений функции: а)y=x2/3+4; б)y=7-x1,5; в) y=2x -1/4; 4)Постройте график функции y=(x-3)1/3+4. 5)Укажите область определения функции: а)y=х-4/5 +8; б)y= 2х/(х1/4-2);