Презентация на тему: Примеры логарифмических уравнений и неравенств

y=log2x-1 (x2-2x-7) Log324-log22xxx=cos30x Логарифмические уравнения и неравенства. Методы решения 900igr.net

Exit Логарифмы в истории Логарифм Логарифмическая функция f(x)=logax Логарифмические уравнения Логарифмические неравенства

Открытие логарифмов - еще одна историческая цепочка знаний, которая связана не только с математикой, но и, казалось бы, совсем не имеющей к ней отношение музыкой. Обращаемся к школе Пифагора (VI-IV вв. до н.э.), открытию в области числовых отношений, связанных с музыкальными звуками. Вся пифагорейская теория музыки основывалась на законах "Пифагора-Архита". 1. Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l / f = a / l (а - коэффициент пропорциональности, характеризующий физические свойства струны). 2. Две звучащие струны дают консонанс (приятное созвучие), если их длины относятся, как 1:2, 2:3, 3:4. Пифагорова гамма была несовершенной, так как не позволяла транспонировать (переводить из тональности в тональность) мелодию. И лишь только в 1700 году немецкий органист А.Веркмайстер осуществил смелое и гениальное решение, разделив октаву (геометрически) на двенадцать равных частей. Какую же роль сыграли здесь логарифмы? Дело в том, что в основе музыкальной гаммы лежит геометрическая прогрессия со знаменателем , которая является иррациональным числом, при нахождении приближенного значения которого используются логарифмы.

Идея логарифма возникла также в Древней Греции. Так, в сочинении "Псамлигт" Архимеда (287 - 212 гг. до н.э.) мы читаем: "Если будет дан ряд чисел в непрерывной пропорции начиная от 1 и если два его члена перемножить, то произведение будет членом того же ряда, настолько удаленным от большего множителя, насколько меньший удален от единицы, и одним членом меньше против того, насколько удалены оба множителя вместе". Здесь под "непрерывной пропорцией" Архимед разумеет геометрическую прогрессию, которую мы записали бы так: 1, а, а2... В этих обозначениях правило, сформулированное Архимедом, будет выражено формулой: am*an = am+n. Историческое развитие понятия логарифма завершилось в XVII веке. В 1614-м в Англии были опубликованы математические таблицы для выполнения приближенных вычислений, в которых использовались логарифмы. Их автором был шотландец Дж.Непер (1550-1617 гг.). В предисловии к своему сочинению Дж.Непер писал: "Я всегда старался, насколько позволяли мои силы и способности, отделаться от трудности и скуки вычислений, докучность которых обыкновенно отпугивает многих от изучения математики". Так вслед за изобретением логарифмов и развитием алгебры иррациональных чисел в музыку вошла равномерная темперация (новый двенадцатизвуковой строй).

Что такое логарифм? logab=c Û ac=b Основное логарифмическое тождество

Основные свойства логарифмов 1) Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей: loga N1·N2 = loga N1 + loga N2  (a > 0, a ≠ 1, N1 > 0, N2 > 0). Замечание. Если N1·N2 > 0, тогда свойство примет вид loga N1·N2 = loga |N1| + loga |N2|   (a > 0, a ≠ 1, N1·N2 > 0). 2) Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя (a > 0, a ≠ 1, N1 > 0, N2 > 0). Замечание. Если , (что равносильно N1N2 > 0) тогда свойство примет вид   (a > 0, a ≠ 1, N1N2 > 0).

3) Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа: loga N k = k loga N         (a > 0, a ≠ 1, N > 0). Замечание. Если k - четное число (k = 2s), то loga N 2s = 2s loga |N|       (a > 0, a ≠ 1, N ≠ 0). 4) Формула перехода к другому основанию:       (a > 0, a ≠ 1, c > 0, c ≠ 1, b > 0), в частности, если b = c, получим (a > 0, a ≠ 1, b > 0, b ≠ 1).

5) Из вышеуказанных свойств вытекают следующие формулы:

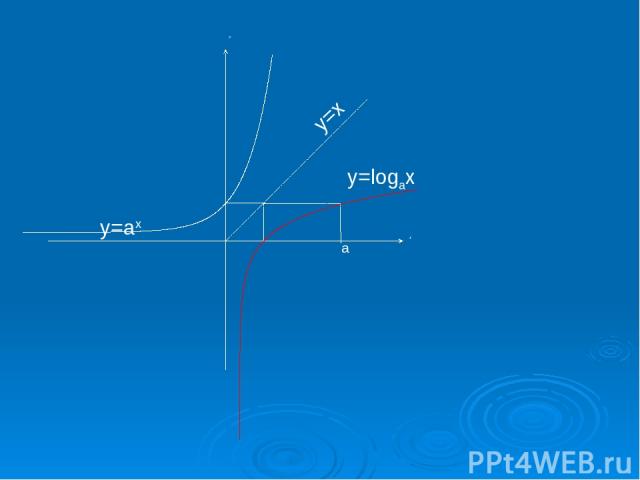
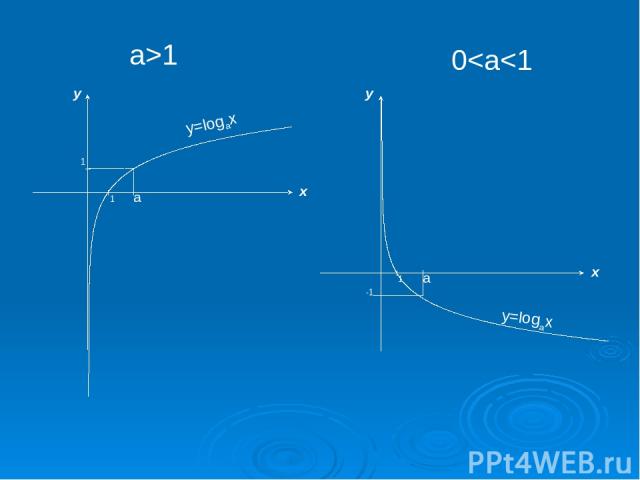
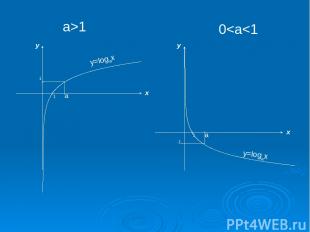
Область определения логарифмической функции есть множество положительных чисел. Область значений логарифмической функции - множество действительных чисел. При a > 1 логарифмическая функция строго возрастает (0 1, то логарифмическая функция выпукла вверх, а если a Î (0;1) - выпукла вниз.

y a>1 0

2) loga f(x) = loga g(x) Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Логарифмические уравнения Решением является x=ab f(x)= g(x), g(x)>0, f(x)>0. f(x)= g(x), g(x)>0, f(x)= g(x), f(x)>0.

4) logh(x) f(x) = logh(x) g(x) Потеря решений при неравносильных переходах loga f(x) = loga g(x)     f(x) = g(x)

Методы решения логарифмических уравнений Использование определения логарифма logab = c Û b = ac Пример log2(5 + 3log2(x - 3)) = 3 Решение 5+3log2(x-3)=23 Û log2(x - 3) = 1 Û x=5

Методы решения логарифмических уравнений Использование свойств логарифма logab = c Û b = ac Пример log3x + log3(x + 3) = log3(x + 24), Решение О.Д.З.: x>0, x(x+3)=x+24 Û x2 + 2x - 24 = 0 Û x={-6;4} Û x>0 Û x=4

Методы решения логарифмических уравнений Метод подстановки f(logax)=0 Û t=logax f(t)=0 Пример lg2x - 3lgx + 2 = 0 Решение lg x = t lgx=1 t2-3t+2=0 Û lgx=2 Û x={10;100}

Пример 5lgx = 50 - xlg5 5lgx = 50 - 5lgx 5lg x = 25 x=100

Методы решения логарифмических уравнений Уравнения, содержащие выражения вида Пример Решение log2(x+2)=t, t2-t-2=0.

Методы решения логарифмических уравнений Метод оценки левой и правой частей Пример log2 (2x – x2 + 15) = x2 – 2x + 5. Решение 1) 2x – x2 + 15 = – (x2 – 2x – 15) = –((x2 – 2x + 1) –1 –15)= = (16 – (x – 1)2)£ 16   log2 (2x – x2 + 15) £ 4. 2) x2 – 2x + 5 = (x2 – 2x + 1) – 1 + 5 = (x – 1)2 + 4 ³ 4; log2 (2x – x2 + 15)=4, x2 – 2x + 5 =4. x=1

Методы решения логарифмических уравнений Использование монотонности функций. Подбор корней. Пример log2 (2x – x2 + 15) = x2 – 2x + 5. Решение 2x–x2+15=t, t>0 x2–2x+5=20–t log2t=20-t y=log2 t – возрастающая, y=20–t – убывающая. Геометрическая интерпретация дает понять, что исходное уравнение имеет единственный корень, который нетрудно найти подбором, t=16. Решив уравнение 2x–x2+15=16, находим, что x=1

1) loga f(x) > loga g(x) Неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Логарифмические неравенства f(x)>g(x)>0, a>1. 01. 0

3) logh(x)f(x)>logh(x)g(x) (h(x)-1)(f(x)-g(x))>0, h(x)>0, f(x)>0, g(x)>0. 4) f(logax)>0 t=logax, f(t)>0.

Методы решения логарифмических неравенств с переменным основанием Быстрое избавление от логарифмов Пример log2x(x2-5x+6)0.

Правило знаков Очевидно, что lg x, как и loga x по любому основанию a > 1, имеет тот же знак, что и число x – 1. В более общем случае от логарифма по произвольному основанию a можно перейти к основанию 10: Таким образом, знак величины loga x совпадает со знаком числа (x – 1)/(a – 1) или (x – 1)(a – 1). 1

Пример log2x(x-4) logx-1(6-x)0, x>0, x≠1/2, x>1,x-1≠1. x (4;5) (5;6)