Презентация на тему: Применение непрерывности

ПРИМЕНЕНИЕ НЕПРЕРЫВНОСТИ И ПРОИЗВОДНОЙ Автор: учитель математики МОУ « Средняя общеобразовательная школа № 30» г. Калуги Григоричева Галина Васильевна 900igr.net

Методом интервалов можно решать неравенства вида: f(х)>0 , f(х) 0 f(х)

Чтобы решить неравенство методом интервалов , следует : Найти область определения функции f Найти значения переменных, которые обращают функцию в нуль Отметить на числовой прямой найденные точки, в порядке возрастания Определить знаки функции в каждом из промежутков Определить ответ 1 Х2+4х-5=0 х1=-5 х2=1 2 х+3=0 Х= -3 4 взяв точку из каждого интервала, подставив её в функцию, определим знаки 5 Ответ (-5;-3], (1; + ).

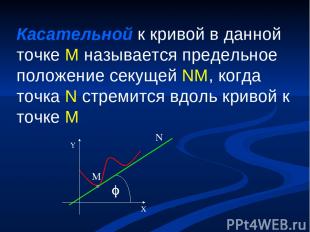
Касательной к кривой в данной точке M называется предельное положение секущей NM, когда точка N стремится вдоль кривой к точке M

Геометрический смысл производной Угловой коэффициент касательной к графику функции равен значению производной этой функции в точке касания: k = tg = lim ∆y/∆x =f’(x) x→0

Уравнение касательной к кривой y = f(x) в заданной точке с абсциссой x0 имеет вид: Где (x0;f (x0))-координаты точки касания, (x;y)- текущие координаты, т.е координаты любой точки, принадлежащей касательной, а f ’(x0) = k = tg - угловой коэффициент касательной.

Алгоритм нахождения уравнения касательной 1. Обозначить абсциссу точки касания буквой а Вычислить f(a) Найти f’(x) и вычислить f’(a) Подставить найденные числа: a, f(a) , f’(a) в уравнение касательной y = f(x0)+f ‘(xo)(x-x0) Пример Составить уравнение касательной к графику функции y = 1/x в точке x = 1 Решение. a = 1 2) f(a) = f(1) = 1/1 =1 3) f’(x) = -1/x2 ; f’(a) = f’(1) = = -1/12 = -1 4) Подставим найденные три числа: a = 1, f (a) = 1,f ’(a) = -1 в уравнение касательной. Получим: y = 1- (x-1) ; y = 2-x. Ответ: y = 2-x

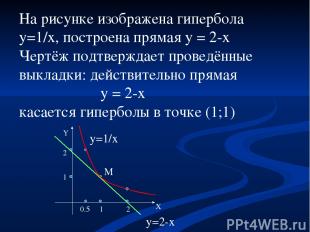
На рисунке изображена гипербола y=1/x, построена прямая y = 2-x Чертёж подтверждает проведённые выкладки: действительно прямая y = 2-x касается гиперболы в точке (1;1) M

Для дифференцируемой в точке х0 функции f при х, мало отличающихся от нуля, её график близок к касательной (проведённой в точке графика с абсциссой х0 ),т.е. при малых х f(х) f(х 0)+f‘(х0) х

Формула f(х) f(х 0)+f‘(х0) х позволяет вывести следующие формулы для приближённых вычислений 1) 1+ х 1+1/2 х 2) (1+ х)n 1+n x

1,06= 1+0,06 1+1/2 0,06=1,03 Вычислим по формуле(1) 1+ х 1+1/2 х значение выражения 1,06 Решение: х=0,06

Решение: х=0,001; n=100 1,001100=(1+0,001)100 1+100 0,001=1,1 (1+ х)n 1+n x значение выражения 1,001100 Вычислим по формуле(2)