Презентация на тему: Предел последовательности

Предел последовательности и предел функции 900igr.net

Предел последовательности Рассмотрим две числовые последовательности (уn) и (хn) и изобразим их члены точками на координатной прямой. (уn): 1, 3, 5, 7, 9,…, 2n – 1,…; (хn): у 0 1 3 5 7 9 11 13 0 1 х

Обрати внимание, что члены последовательности (хn) как бы «сгущаются» около точки 0, а у последовательности (уn) такой точки нет. В подобных случаях говорят, что последовательность (хn) сходится, а последовательность (уn) расходится. Чтобы узнать является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности, введем следующее понятие.

Определение 1. Пусть а – точка прямой, а r – положительное число. Интервал (а-r; a+r) называют окрестностью точки а, а число r – радиусом окрестности. Пример. (3,97; 4,03) – окрестность точки 4, радиус равен 0,03. х a-r a+r a

В математике «точку сгущения» для членов заданной последовательности принято называть «пределом последовательности». Определение 2. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера. Обозначение: 1. (уn стремится к b или уn сходится к b); 2. (предел последовательности уn при стремлении n к бесконечности равен b)

Примеры 1. ; 2. Если , то ; Если , то последовательность расходится. 3. .

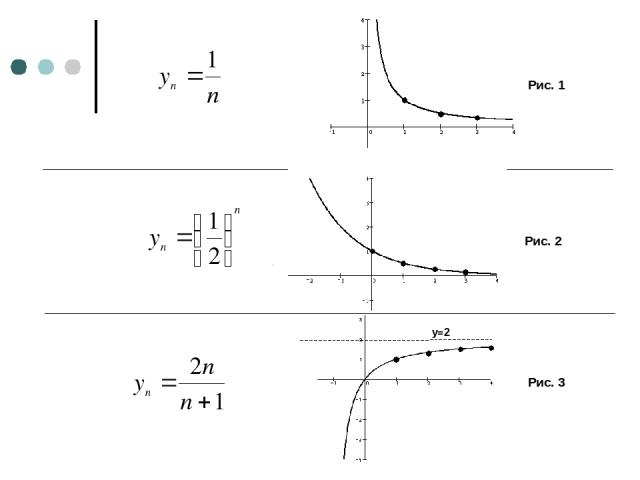
Обсудим результаты, полученные в примерах с геометрической точки зрения. Для этого построим графики последовательностей:

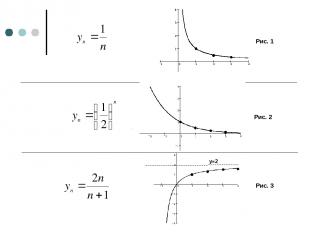
Рис. 1 Рис. 2 Рис. 3

Обрати внимание, что на всех трех рисунках точки графика, по мере их ухода вправо, все ближе и ближе подходят к некоторой горизонтальной прямой: на рис 1 – к прямой у=0, на рис 2 – к прямой у=0, на рис 3 – к прямой у=2. Каждую из этих прямых называют горизонтальной асимптотой графика.

Вообще равенство означает, что прямая является горизонтальной асимптотой графика последовательности, т.е. графика функции

Свойства сходящихся последовательностей Свойство 1. Если последовательность сходится, то только к одному пределу. Свойство 2. Если последовательность сходится, то она ограничена, обратное неверно. Свойство 3. Если последовательность монотонна и ограниченна, то она сходится.

Вычисление пределов последовательности I. Предел стационарной последовательности равен значению любого члена последовательности:

Пусть , . II. Предел суммы равен сумме пределов: Пример.

III. Предел произведения равен произведению пределов: Пример.

IV. Предел частного равен частному от пределов (при условиях, что : Пример.

V. Постоянный множитель можно вынести за знак предела: Пример.

Сумма бесконечной геометрической прогрессии Рассмотрим бесконечную геометрическую прогрессию Вычислим суммы двух, трех и т.д. членов прогрессии:

Получилась последовательность Она может сходиться или расходиться. Если последовательность сходится к пределу S, то число S называется суммой геометрической прогрессии. Если расходится, то о сумме геометрической прогрессии не говорят. Формула суммы первых n членов геометрической прогрессии следующая:

Теорема. Если знаменатель геометрической прогрессии удовлетворяет неравенству , то сумма прогрессии вычисляется по формуле Пример.

Предел функции Предел функции на бесконечности. Предел функции в точке.

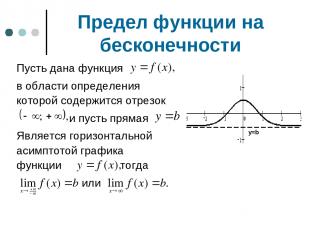
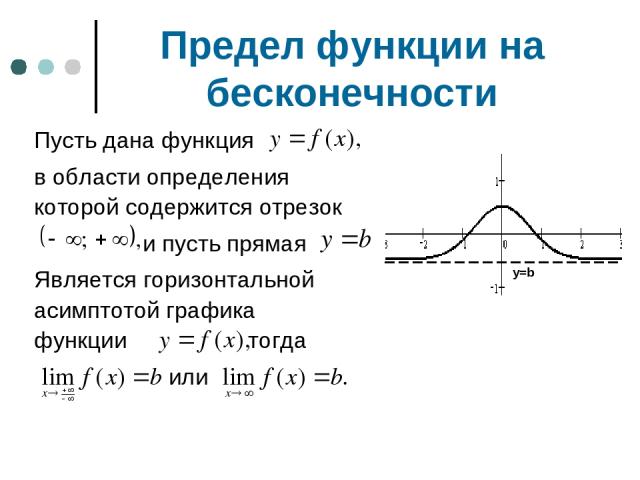
Предел функции на бесконечности Пусть дана функция в области определения которой содержится отрезок и пусть прямая Является горизонтальной асимптотой графика функции тогда или y=b

Вычисление предела функции на бесконечности Для справедливо соотношение

2. Если ,то а) предел суммы равен сумме пределов: б) предел произведения равен произведению пределов:

в) предел частного равен частному от пределов: г) постоянный множитель можно вынести за знак предела: Пример.

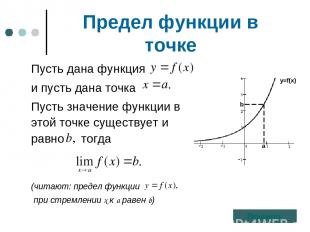
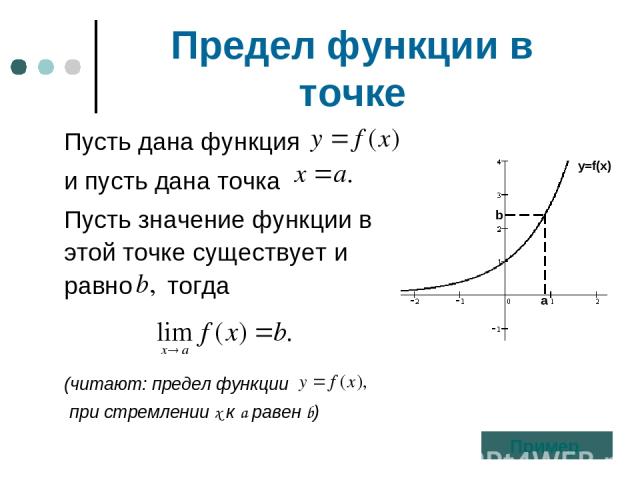
Предел функции в точке Пусть дана функция и пусть дана точка Пусть значение функции в этой точке существует и равно тогда (читают: предел функции при стремлении х к а равен b) Пример. y=f(x) b a

Проверь себя! Дорогой друг, теперь тебе предстоит проверить свои знания. Для этого нужно ответить на тест, который состоит из 10 вопросов, К каждому вопросу дается на выбор три ответа, один из которых верный. Желаю удачи!

1. Окрестность какой точки является интервал (2,1; 2,3)? а) 2; б) 2,15; в) 2,2.

Неверно! Попробуй еще!

Верно! Дальше!

а) 2; б) 1; в) 1,5. 2. Интервал (7; 5) окрестность точки 6, чему равен радиус этой окрестности?

Неверно! Попробуй еще!

Верно! Дальше!

3. Последовательность является: а) сходящейся; б) расходящейся; в) ничего определенного сказать нельзя.

Неверно! Попробуй еще!

Верно! Дальше!

4. Число b называют пределом последовательности , если: а) в любой окрестности точки b содержатся все члены последовательности, начиная с некоторого номера; б) в любой окрес тности точки b содержатся некоторые члены последовательности, начиная с некоторого номера; в) в любой окрестности точки b не содержатся члены последовательности.

Неверно! Попробуй еще!

Верно! Дальше!

5. Равенство означает, что прямая является для графика : а) горизонтальной асимптотой; б) вертикальной асимптотой; в) наклонной асимптотой.

Неверно! Попробуй еще!

Верно! Дальше!

6. Какое из утверждений верно? а) если последовательность имеет предел, то она монотонна; б) если последовательность не монотонна, то она не имеет предела; в) если последовательность ограничена, то она имеет предел.

Неверно! Попробуй еще!

Верно! Дальше!

7. Предел последовательности равен: а) 0; б) 1; в) 2.

Неверно! Попробуй еще!

Верно! Дальше!

8. Сумма геометрической прогрессии равна: а) 40; б) 41; в) 40,5.

Неверно! Попробуй еще!

Верно! Дальше!

9. Найти а) 0; б) ; в) .

Неверно! Попробуй еще!

Верно! Дальше!

10. Найти а) 1; б) 3; в) 2.

Неверно! Попробуй еще!

Верно! Дальше!

Пример. Найти предел последовательности Решение.

Пример. Вычислить Решение. Делим числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n, т.е. на n2.

Пример. Найти предел последовательности Решение.

Пример. Найти предел последовательности Решение.

Пример. Вычислить Решение. Ответ: -1,5.

Дано (уn)= Доказать, что Решение. Возьмем любую окрестность точки 0, с радиусом r. Подберем натуральное число n0 так, чтобы выполнялось неравенство Если например, r=0,001, то в качестве n0 можно взять 1001; если , то n0=5774. Член данной последовательности с номером n0 попадает в выбранную окрестность точки 0. В этой же окрестности будут находиться все последующие члены, тогда по определению 2 следует, что

Пример. Найти сумму геометрической прогрессии Решение. Здесь Так как знаменатель прогрессии удовлетворяет неравенству , то воспользовавшись формулой , получим Ответ:

Если , то Пусть , получим По аналогии с первым примером, здесь последовательность сходится к 0, значит . Если , то последовательность расходится. Пусть , получим Эта последовательность явно не имеет предела, значит она расходится.

Дана последовательность найти ее предел. Выполним некоторые преобразования выражения : Это значит, в частности, что и т. д., Данную последовательность перепишем так: Видно, что «точкой сгущения» является 2, значит

Рассмотрим пример. Дана последовательность (хn)=1, 2, 3, 1, 2, 3,…, 1, 2, 3,…. Эта последовательность ограничена, но не является сходящейся.

Пример. Вычислить Решение. Разделим числитель и знаменатель дроби почленно на х2: Ответ: 2.