![Функция y=sinx и её свойства. 1. D(f)=(-∞,+∞). 2.Функция нечётна. 3.Возрастает на отрезке [0,∏/2] убывает на отрезке [∏/2,∏]. 4.Ограничена сверху и снизу. 5.yнаим.=-1; yнаиб.=1. 6.Функция непрерывна. 7.E(f)= [-1;1].](https://fs3.ppt4web.ru/images/132073/181381/640/img2.jpg "Функция y=sinx и её свойства. 1. D(f)=(-∞,+∞). 2.Функция нечётна. 3.Возрастает на отрезке [0,∏/2] убывает на отрезке [∏/2,∏]. 4.Ограничена сверху и снизу. 5.yнаим.=-1; yнаиб.=1. 6.Функция непрерывна. 7.E(f)= [-1;1].")
![Функция y=cosx и её свойства. 1.D(f)=(-∞;+∞). 2.Чётная функция. 3.Убывает на отрезке [0,∏], возрастает на отрезке [∏,2∏]. 4.Функция ограничена сверху и снизу. 5.yнаим=-1; yнаиб=1. 6.Функция непрерывна. 7.E(f)=[-1;1].](https://fs3.ppt4web.ru/images/132073/181381/640/img8.jpg "Функция y=cosx и её свойства. 1.D(f)=(-∞;+∞). 2.Чётная функция. 3.Убывает на отрезке [0,∏], возрастает на отрезке [∏,2∏]. 4.Функция ограничена сверху и снизу. 5.yнаим=-1; yнаиб=1. 6.Функция непрерывна. 7.E(f)=[-1;1].")
Презентация на тему: Построить график функции
Графики и функций y=m sinx+n и y=m cosx+n. Выполнил: Кадет 52 учебной группы Лёвин Алексей. 900igr.net
Содержание: 1. Функция y=sin x, её свойства и разновидности; 2. Функция y=cos x, её свойства и разновидности; 3. Примеры задач. 4. Закончить просмотр.
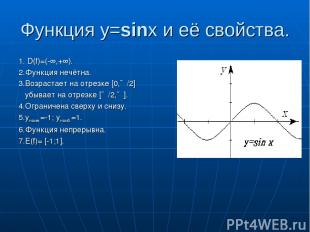
Функция y=sinx и её свойства. 1. D(f)=(-∞,+∞). 2.Функция нечётна. 3.Возрастает на отрезке [0,∏/2] убывает на отрезке [∏/2,∏]. 4.Ограничена сверху и снизу. 5.yнаим.=-1; yнаиб.=1. 6.Функция непрерывна. 7.E(f)= [-1;1].
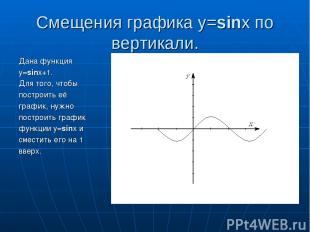
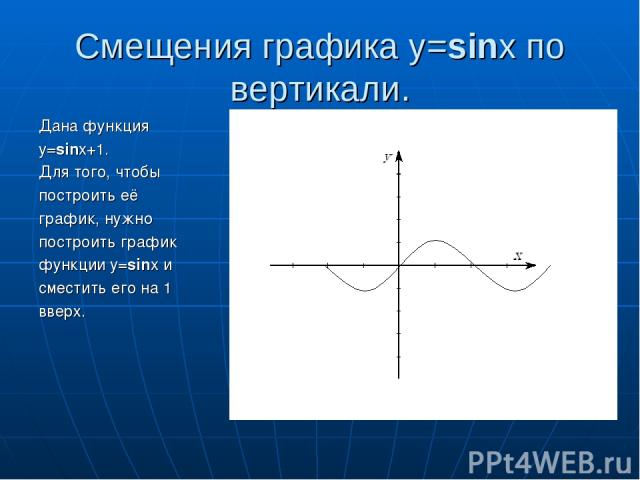
Смещения графика y=sinx по вертикали. Дана функция y=sinx+1. Для того, чтобы построить её график, нужно построить график функции y=sinx и сместить его на 1 вверх.
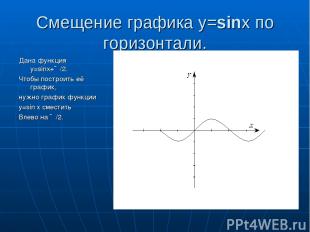
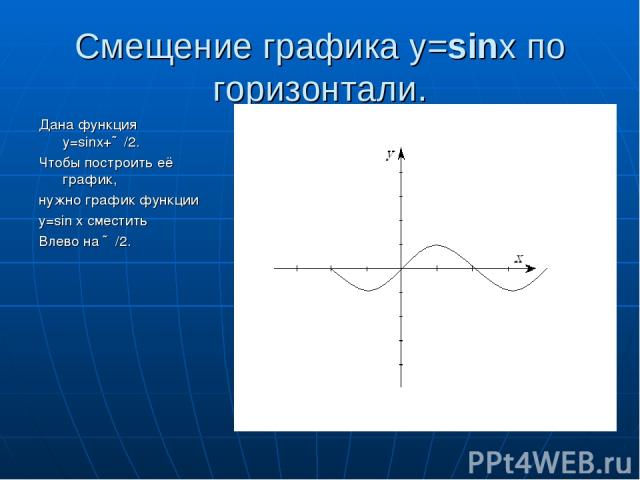
Смещение графика y=sinx по горизонтали. Дана функция y=sinx+∏/2. Чтобы построить её график, нужно график функции y=sin x сместить Влево на ∏/2.
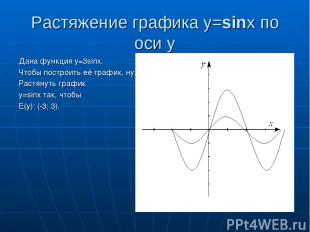
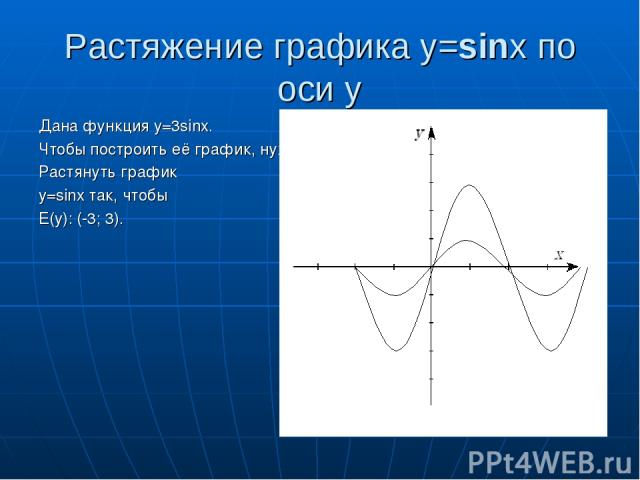
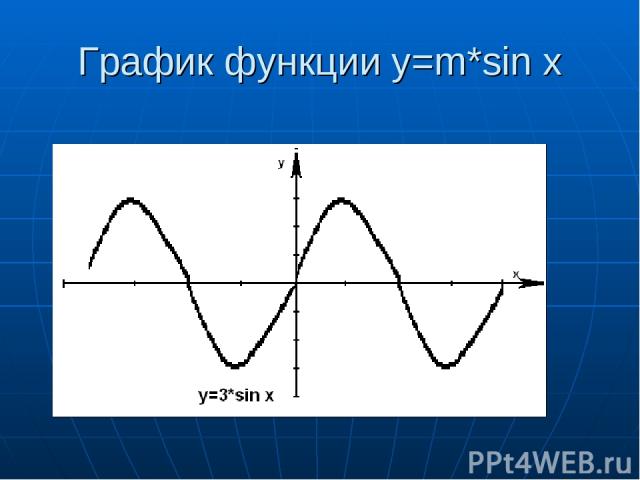
Растяжение графика y=sinx по оси y Дана функция y=3sinx. Чтобы построить её график, нужно Растянуть график y=sinx так, чтобы E(y): (-3; 3).
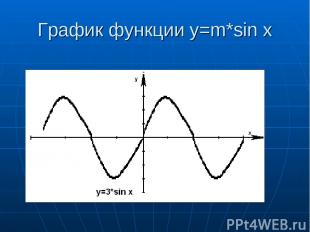
График функции y=m*sin x
Для того, чтобы вернуться содержанию нажмите сюда. Чтобы продолжить нажмите на л. Кнопку мыши. К СОДЕРЖАНИЮ
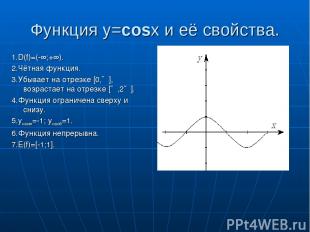
Функция y=cosx и её свойства. 1.D(f)=(-∞;+∞). 2.Чётная функция. 3.Убывает на отрезке [0,∏], возрастает на отрезке [∏,2∏]. 4.Функция ограничена сверху и снизу. 5.yнаим=-1; yнаиб=1. 6.Функция непрерывна. 7.E(f)=[-1;1].
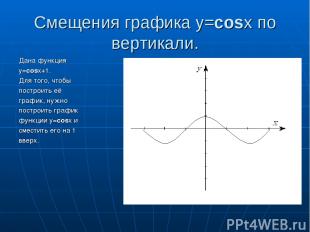
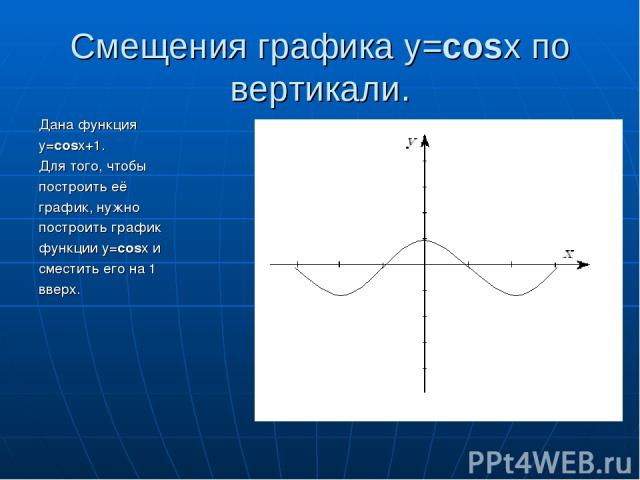
Смещения графика y=cosx по вертикали. Дана функция y=cosx+1. Для того, чтобы построить её график, нужно построить график функции y=cosx и сместить его на 1 вверх.
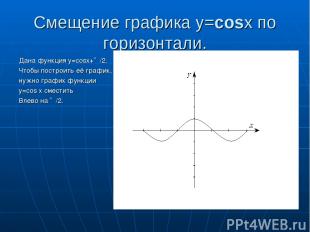
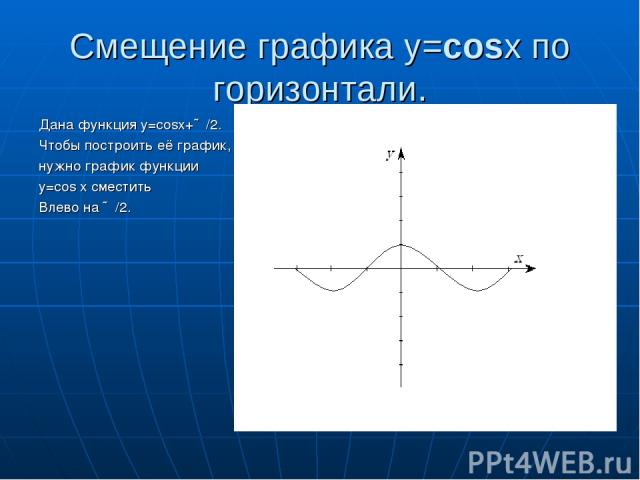
Смещение графика y=cosx по горизонтали. Дана функция y=cosx+∏/2. Чтобы построить её график, нужно график функции y=cos x сместить Влево на ∏/2.
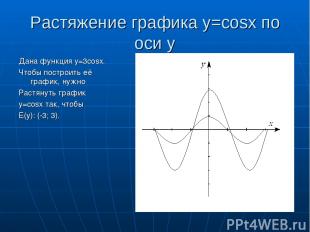
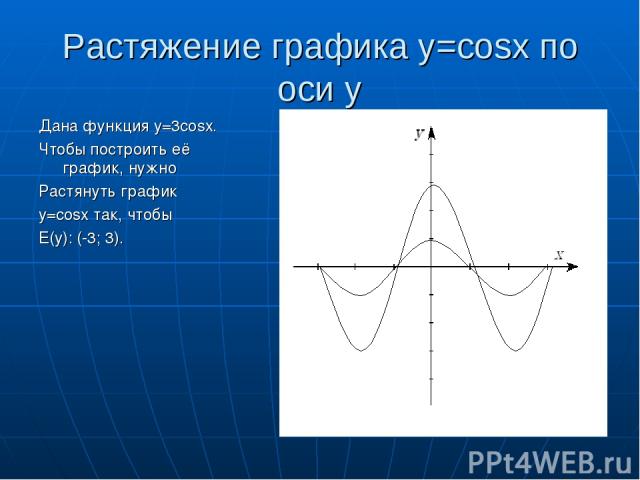
Растяжение графика y=cosx по оси y Дана функция y=3cosx. Чтобы построить её график, нужно Растянуть график y=cosx так, чтобы E(y): (-3; 3).
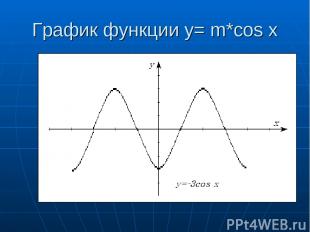
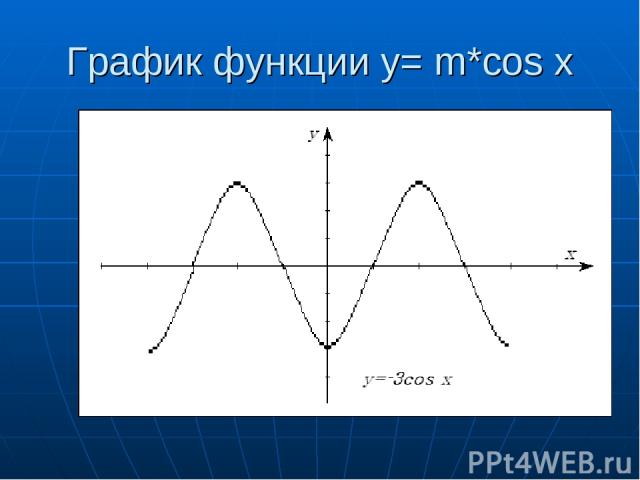
График функции y= m*cos x
Чтобы вернуться К содержанию нажмите сюда. Чтобы перейти к примерам задач щёлкните л. кнопкой мышки. К СОДЕРЖАНИЮ
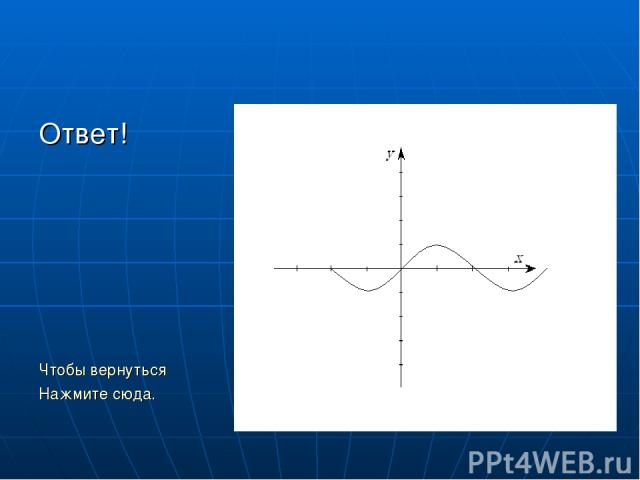
Самостоятельная работа. Дана функция: y=sin (x+∏/2). Постройте график функции. Ответ. Чтобы вернуться к содержанию нажмите сюда. К СОДЕРЖАНИЮ
Lelik productions. 2006год.
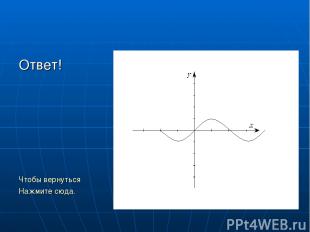
Ответ! Чтобы вернуться Нажмите сюда.
