Презентация на тему: Построение графиков

Построение графиков функций, уравнений и соответствий ЧУДАЕВА Е. В. учитель математики, г. Инсар, СОШ №1 Элективный курс, 10 класс 900igr.net

прояснить и дополнить школьный материал, связанный с функциями и построением их графического изображения, представить систематизацию функций не по видам, а по методам построения их графиков. Цель элективного курса

знакомство учащихся с методами решения различных по формулировке нестандартных задач, связанных с построениями графиков соответствий; привитие навыков употребления функционально-графического метода при решении задач; расширение и углубление знаний по математике по программному материалу. Задачи элективного курса

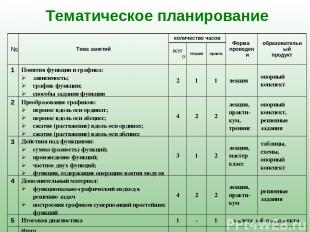
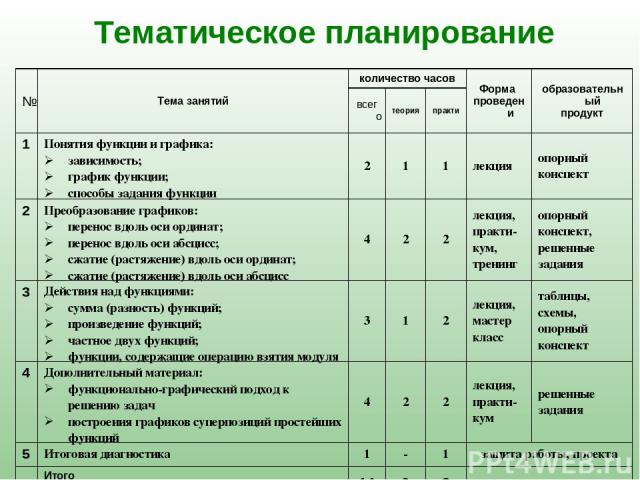
Тематическое планирование № Тема занятий количество часов Форма проведени образовательный продукт всего теория практи 1 Понятия функции и графика: зависимость; график функции; способы задания функции 2 1 1 лекция опорный конспект 2 Преобразование графиков: перенос вдоль оси ординат; перенос вдоль оси абсцисс; сжатие (растяжение) вдоль оси ординат; сжатие (растяжение) вдоль оси абсцисс 4 2 2 лекция, практи- кум, тренинг опорный конспект, решенные задания 3 Действия над функциями: сумма (разность) функций; произведение функций; частное двух функций; функции, содержащие операцию взятия модуля 3 1 2 лекция, мастер класс таблицы, схемы, опорный конспект 4 Дополнительный материал: функционально-графический подход к решению задач построения графиков суперпозиций простейших функций 4 2 2 лекция, практи- кум решенные задания 5 Итоговая диагностика 1 - 1 защита работы, проекта Итого 14 6 8

Параллельный перенос вдоль оси OY Параллельный перенос вдоль оси OX Растяжение (сжатие) в k раз вдоль оси OY Растяжение (сжатие) в k раз вдоль оси OX Симметричное отображение относительно оси OX Симметричное отображение относительно оси OY Содержание

Параллельный перенос вдоль оси ординат Содержание

Параллельный перенос вдоль оси абсцисс Содержание

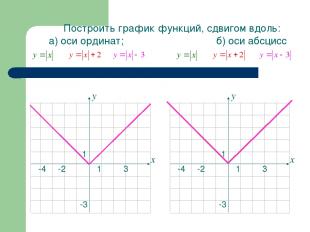
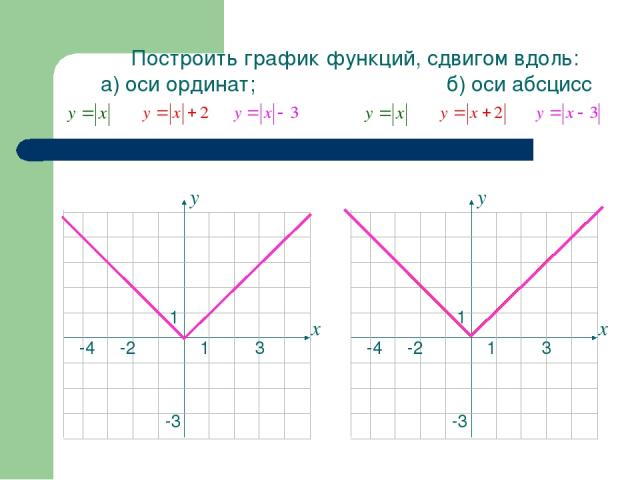
1 3 -4 1 -3 -2 х у у Построить график функций, сдвигом вдоль: а) оси ординат; б) оси абсцисс

Растяжение (сжатие) в k раз вдоль оси ординат Содержание

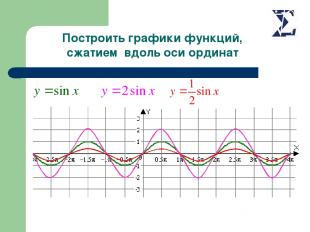
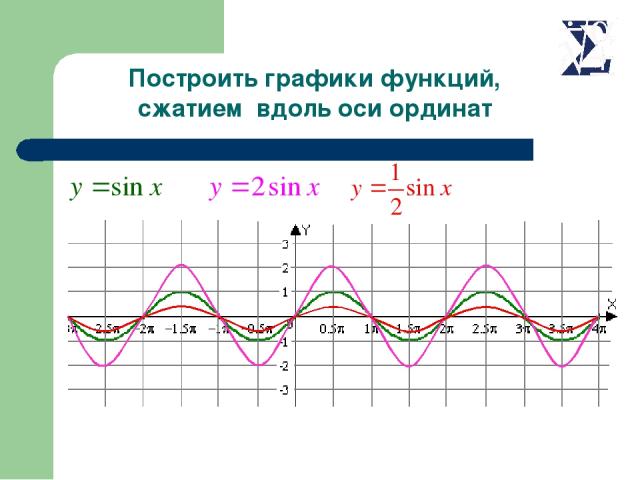
Построить графики функций, сжатием вдоль оси ординат

Растяжение (сжатие) в k раз вдоль оси абсцисс Содержание

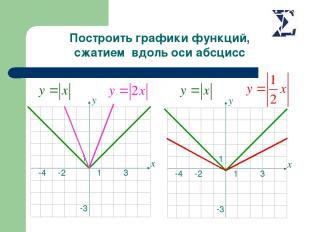
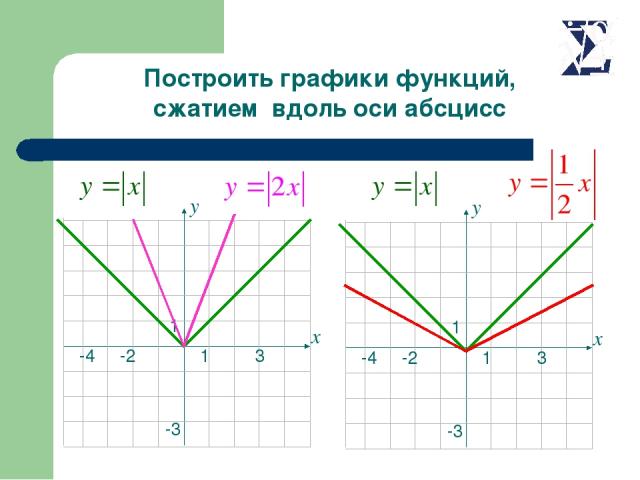
Построить графики функций, сжатием вдоль оси абсцисс

Симметричное отображение относительно оси абсцисс Содержание

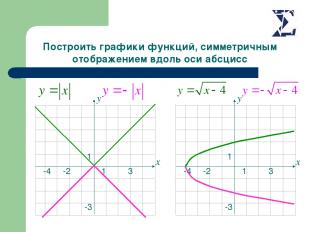
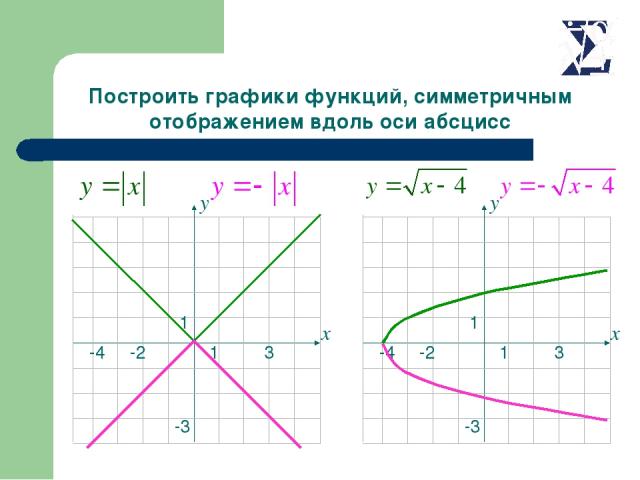
Построить графики функций, симметричным отображением вдоль оси абсцисс

Симметричное отображение относительно оси ординат Содержание

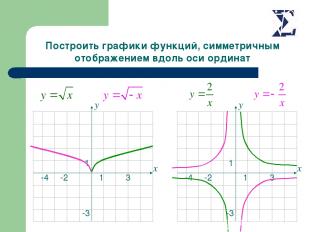
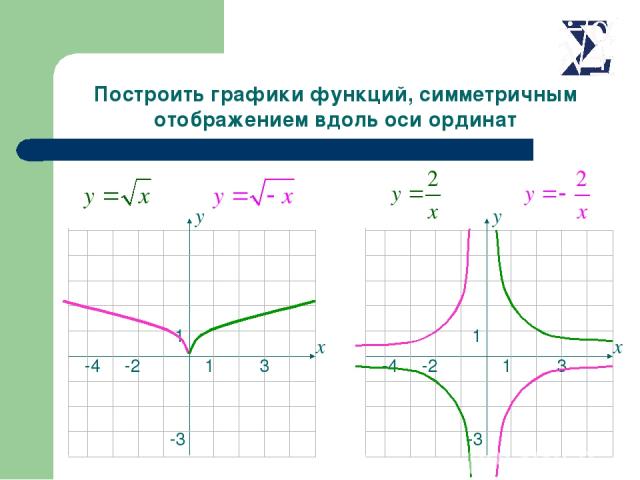
Построить графики функций, симметричным отображением вдоль оси ординат

Построение графика Содержание

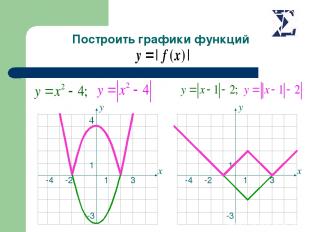
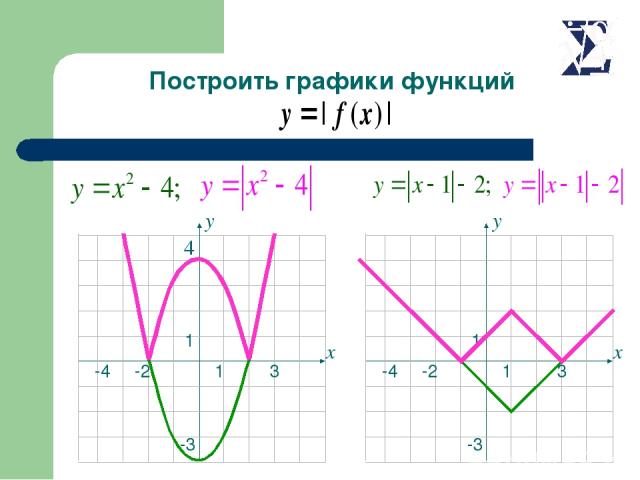
Построить графики функций 4

Построение графика Содержание

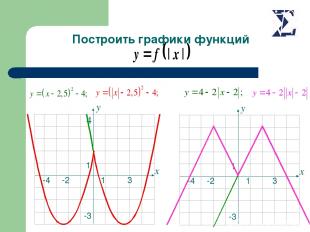
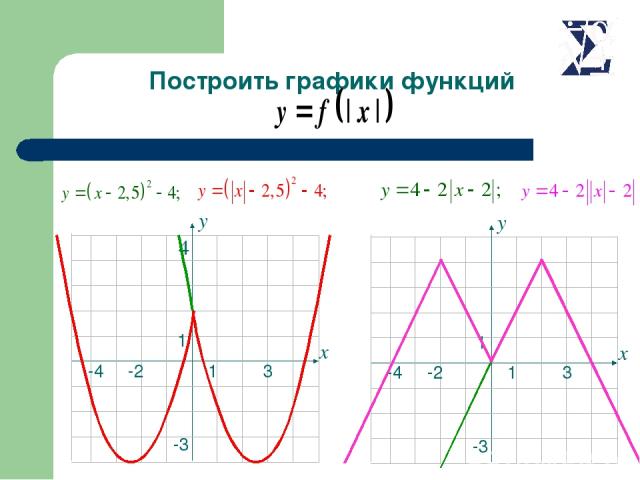
4 Построить графики функций

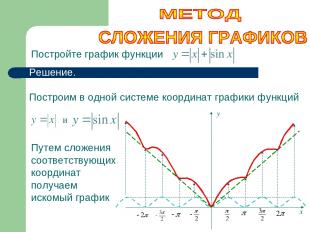
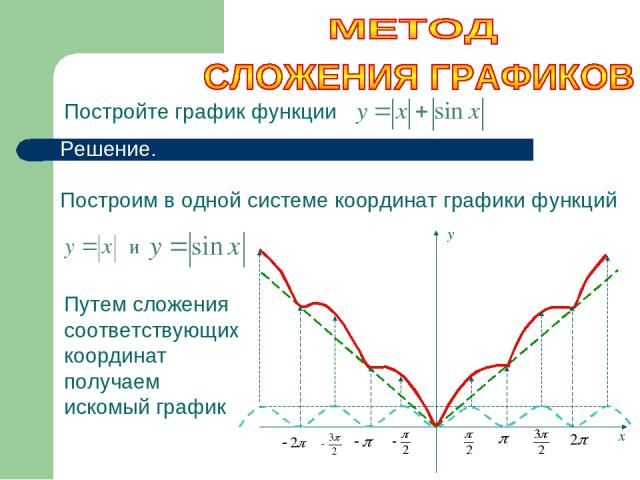
Постройте график функции Решение. Построим в одной системе координат графики функций Путем сложения соответствующих координат получаем искомый график х у

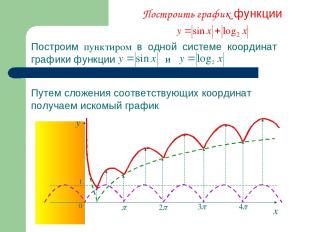
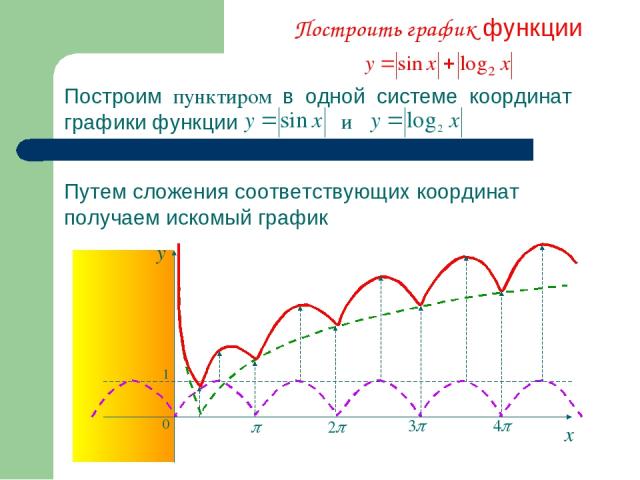
Построить график функции Построим пунктиром в одной системе координат графики функции и Путем сложения соответствующих координат получаем искомый график х у 1 0

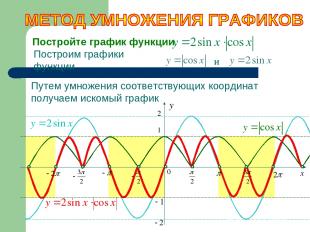
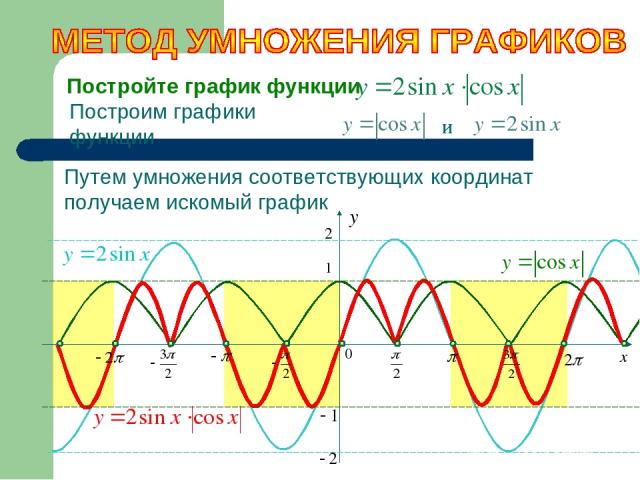
Постройте график функции Построим графики функции и Путем умножения соответствующих координат получаем искомый график

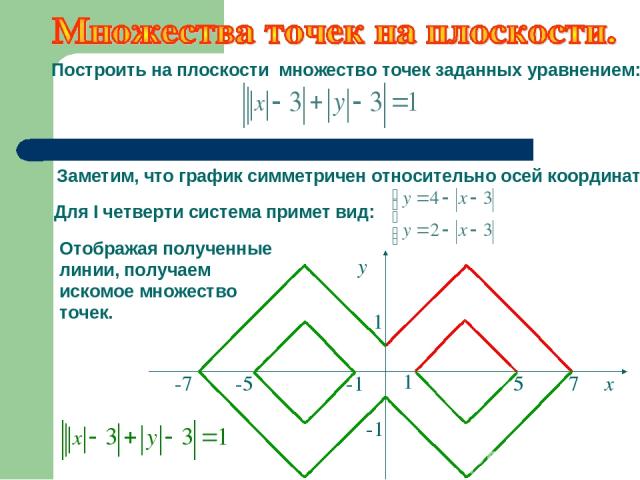
Отображая полученные линии, получаем искомое множество точек. Построить на плоскости множество точек заданных уравнением: 1 у 1 -1 -1 -7 -5 5 7 х Заметим, что график симметричен относительно осей координат. Для I четверти система примет вид:

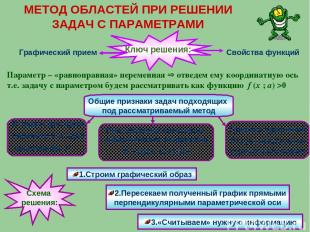
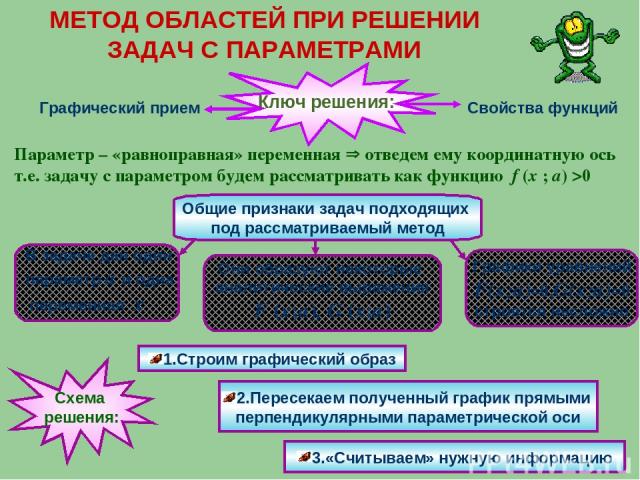
МЕТОД ОБЛАСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ С ПАРАМЕТРАМИ Ключ решения: Графический прием Свойства функций Параметр – «равноправная» переменная отведем ему координатную ось т.е. задачу с параметром будем рассматривать как функцию f (x ; a) >0 Общие признаки задач подходящих под рассматриваемый метод В задаче дан один параметр а и одна переменная х Они образуют некоторые аналитические выражения F (x;a), G (x;a) Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно 1.Строим графический образ 2.Пересекаем полученный график прямыми перпендикулярными параметрической оси 3.«Считываем» нужную информацию Схема решения:

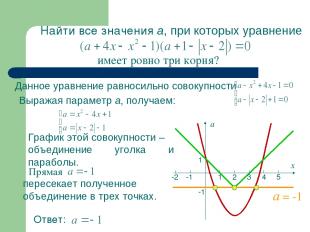
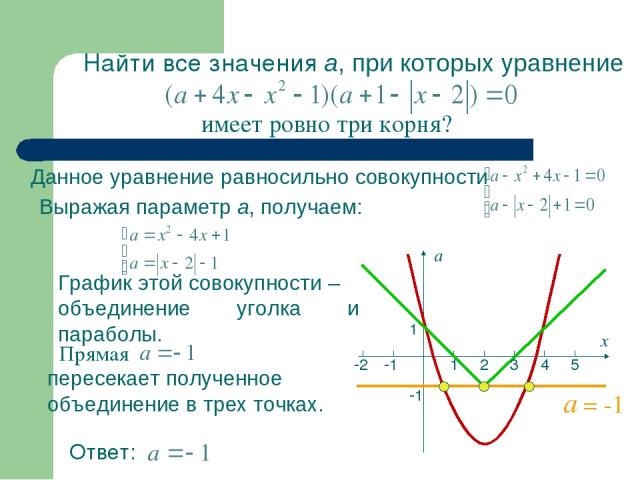
Найти все значения а, при которых уравнение Данное уравнение равносильно совокупности Выражая параметр а, получаем: График этой совокупности – объединение уголка и параболы. пересекает полученное объединение в трех точках. имеет ровно три корня? Ответ: 1 2 3 4 5 -1 -2 -1 1 х а а = -1 Прямая

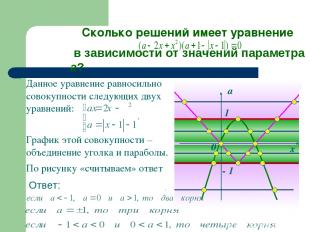
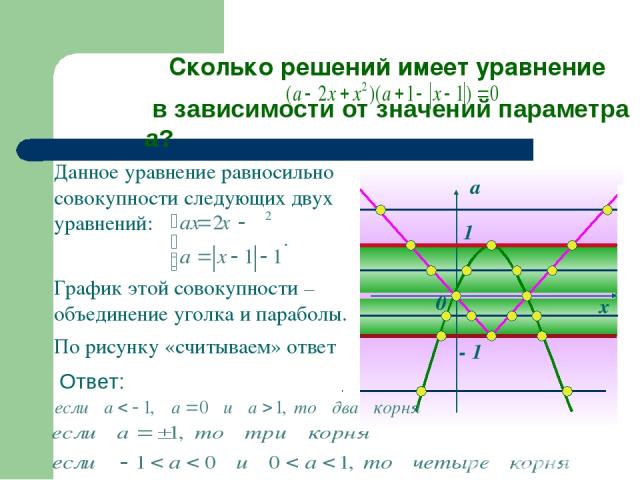
Данное уравнение равносильно совокупности следующих двух уравнений: По рисунку «считываем» ответ х а 0 - 1 1 Ответ: Сколько решений имеет уравнение в зависимости от значений параметра а? График этой совокупности –объединение уголка и параболы.

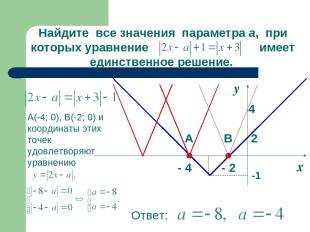
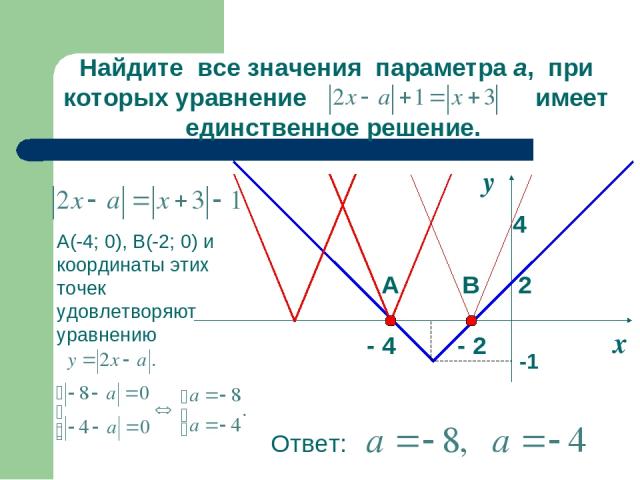
х у - 2 - 4 4 Найдите все значения параметра а, при которых уравнение имеет единственное решение. 2 А В А(-4; 0), В(-2; 0) и координаты этих точек удовлетворяют уравнению -1

(«переход» метода интервалов с прямой на плоскость) 1. ОДЗ 2. Граничные линии 3. Координатная плоскость 4. Знаки в областях 5.Ответ по рисунку. 1.ОДЗ 2. Корни 3. Ось 4. Знаки на интервалах 5. Ответ. Метод интервалов: Метод областей: ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ

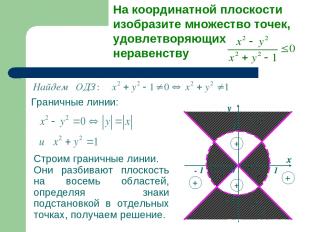
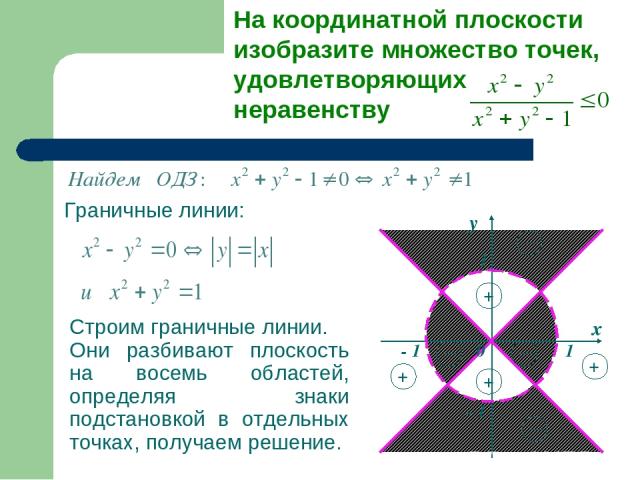
Граничные линии: Строим граничные линии. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение. - 1 - 1 1 1 х у 0 На координатной плоскости изобразите множество точек, удовлетворяющих неравенству

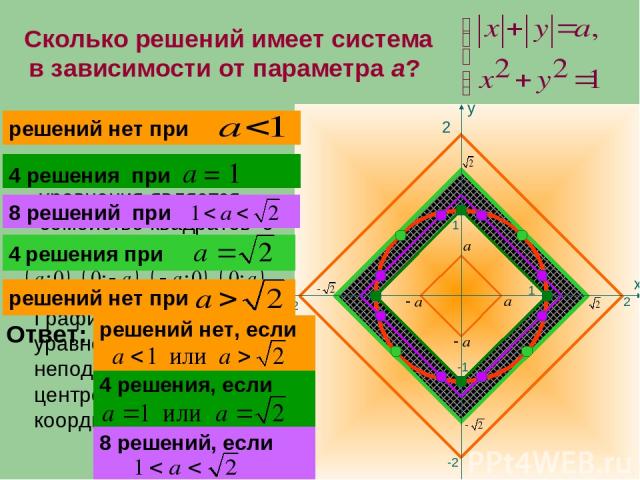
Сколько решений имеет система в зависимости от параметра а? 2 -2 2 -2 1 -1 1 Графиком второго уравнения является неподвижная окружность с центром в начале координат и радиусом 1 4 решения при а = 1 Ответ: решений нет, если 8 решений, если 4 решения, если

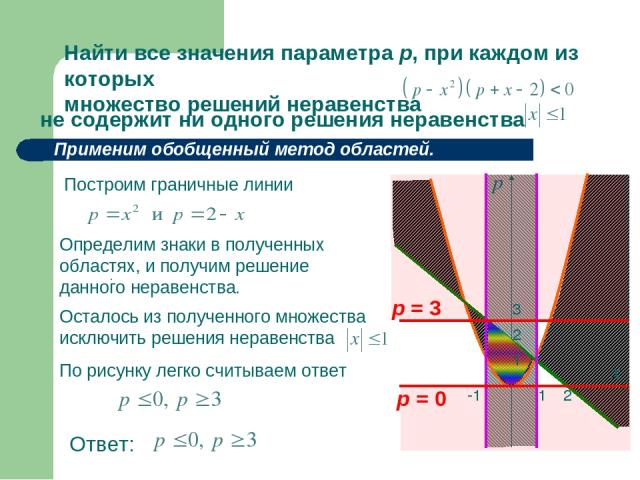
Найти все значения параметра р, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства . Применим обобщенный метод областей. Определим знаки в полученных областях, и получим решение данного неравенства. По рисунку легко считываем ответ Ответ: Построим граничные линии р = 3 р = 0 -1 1 2 3 1 2

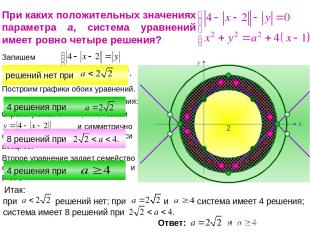
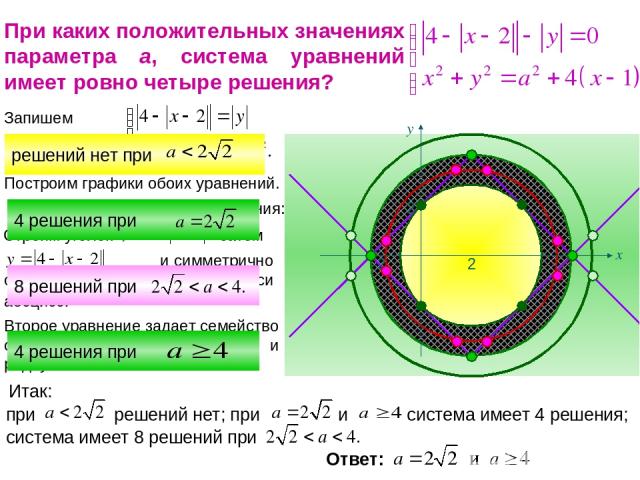
При каких положительных значениях параметра а, система уравнений имеет ровно четыре решения? и симметрично отображаем относительно оси абсцисс. Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.

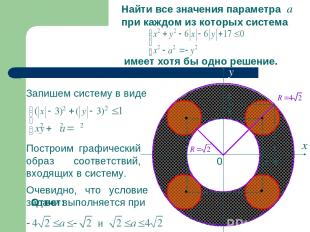
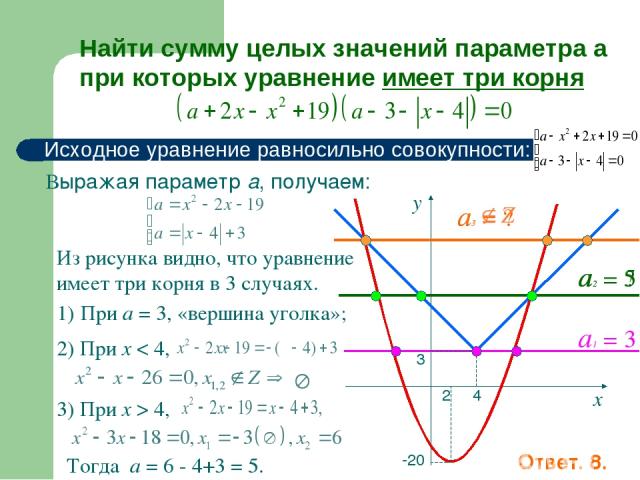
Найти все значения параметра а при каждом из которых система имеет хотя бы одно решение. Запишем систему в виде Построим графический образ соответствий, входящих в систему. 3 3 4 4 Очевидно, что условие задачи выполняется при Ответ:

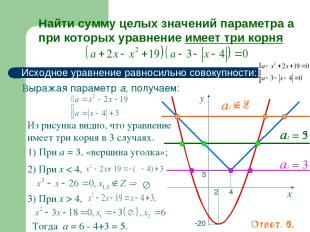
При а = 3, «вершина уголка»; Найти сумму целых значений параметра а при которых уравнение имеет три корня Исходное уравнение равносильно совокупности: Выражая параметр а, получаем: Из рисунка видно, что уравнение имеет три корня в 3 случаях. 3 4 -20 2 х у а1 = 3 а2 = ? а3 = ? Тогда а = 6 - 4+3 = 5. Ответ. 8. 2) При x < 4, 3) При х > 4, а2 = 5