Презентация на тему: Квадратичная функция

Определение Определение График Свойства функции График и свойства функции у = ах2 Сдвиг графика у = ах2 Способы построения параболы Квадратичная функция в заданиях ГИА Примеры и комментарии Задания ГИА

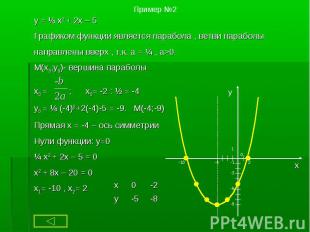
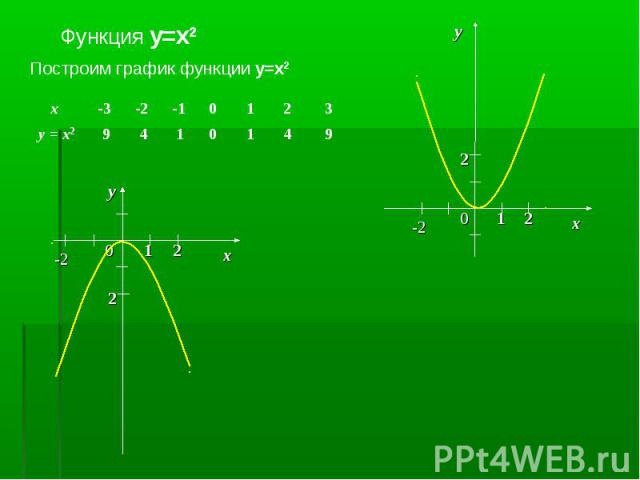
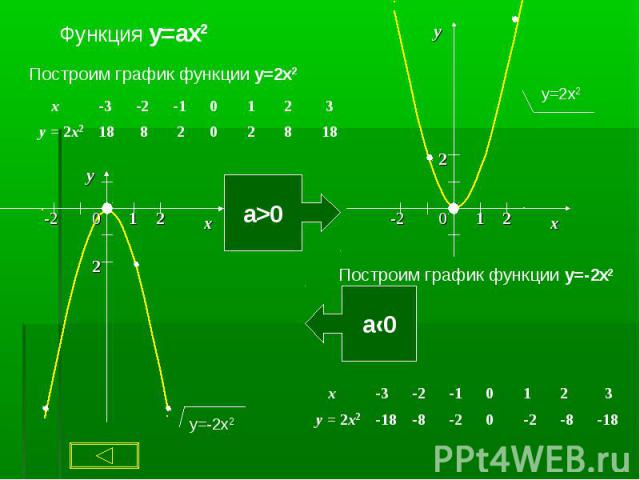
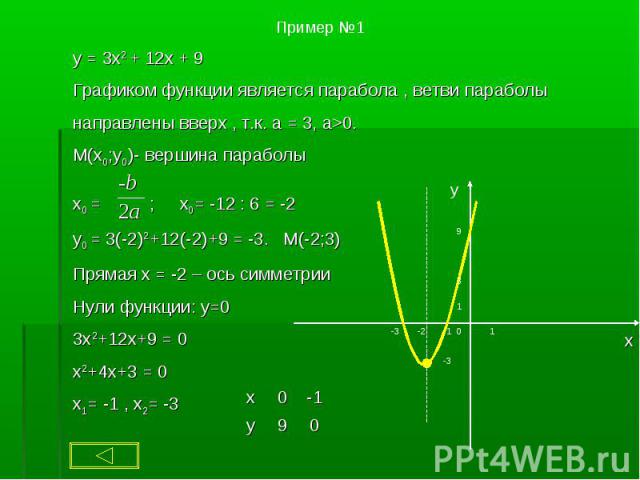
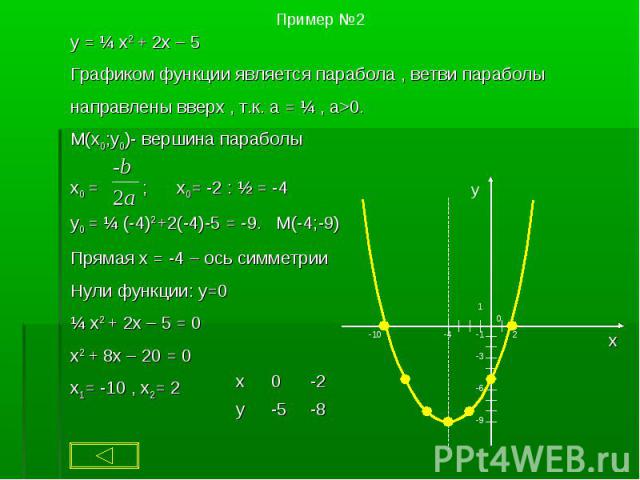
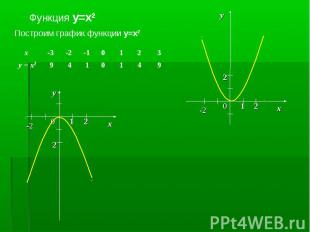
Квадратичной функцией называют функцию, которую можно задать формулой вида Квадратичной функцией называют функцию, которую можно задать формулой вида y = ax2 + bx + c, где a, b и с - некоторые числа, причём а ≠ 0.

y = ax2 + bx + c, y = ax2 + bx + c,

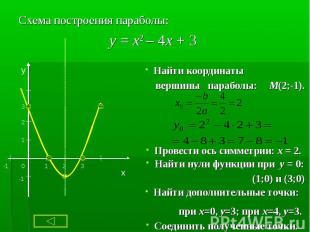
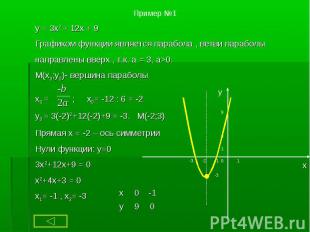
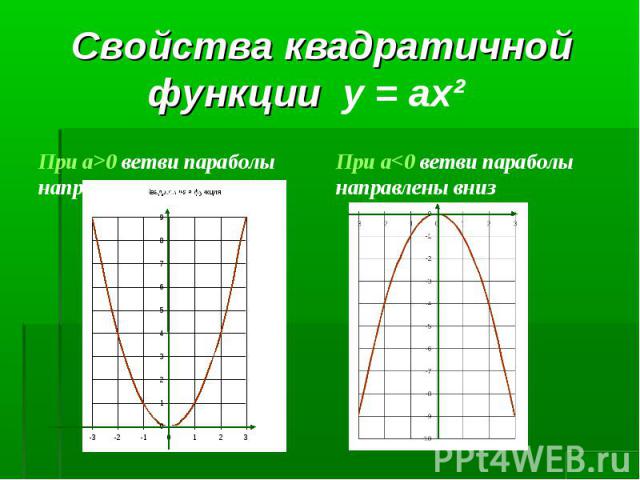
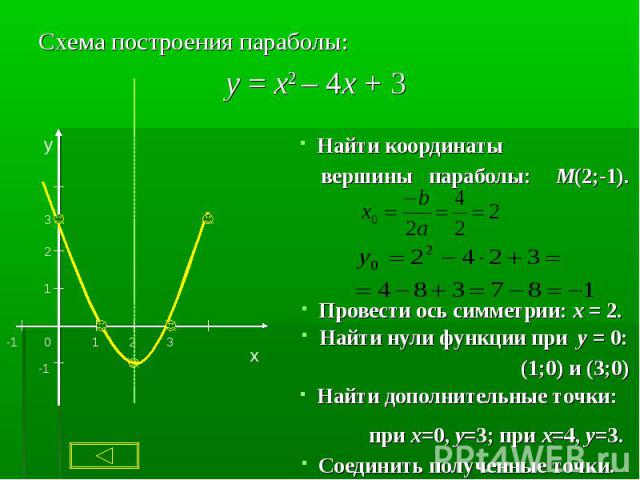
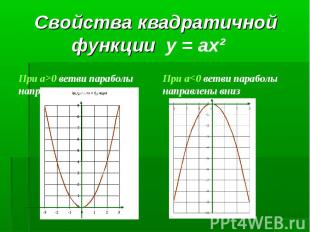
1. Нули функции: y=0 (пересечения с осью Ох) 1. Нули функции: y=0 (пересечения с осью Ох) 2.Точки пересечения с осью Оy 3.Возрастание функции( если X2>X1, то f (X2)>f (X1)): с возрастанием аргумента увеличивается значение функции. Убывание функции( если X2>X1, то f (X2)<f (X1)): с возрастанием аргумента уменьшается значение функции - аргумент и функция связаны противоположными знаками. 4. Промежутки знакопостоянства : f (x) >0 и f (x)<0. 5. Непрерывность функции (разрыв - нельзя провести график не отрываясь). 6. Наибольшее и наименьшее значение.

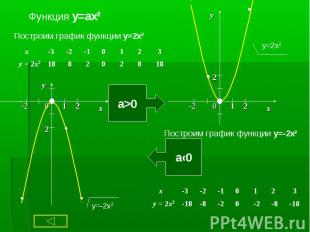
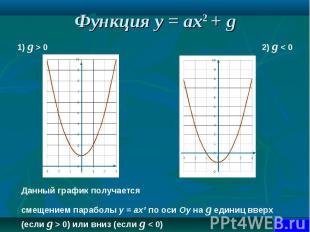
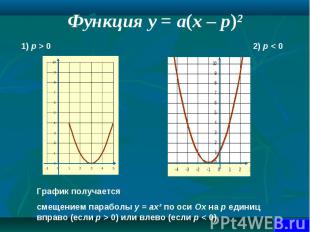
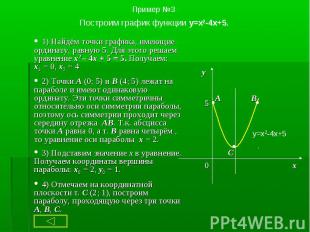
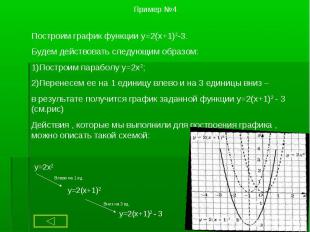
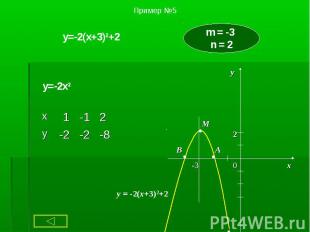
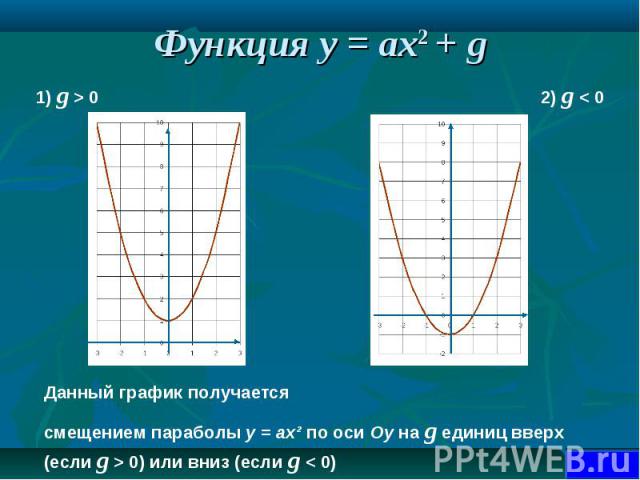
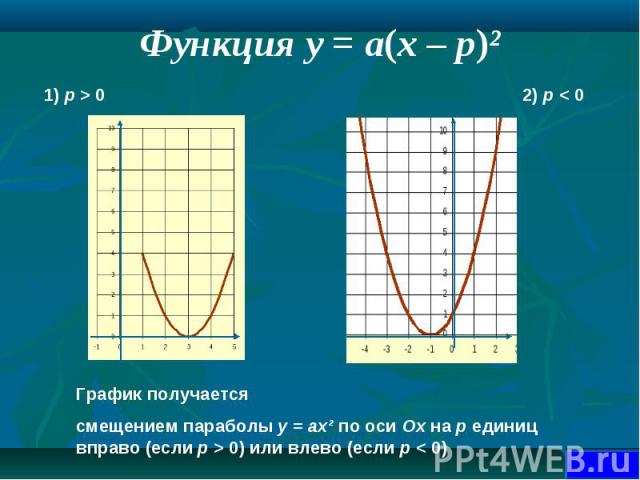
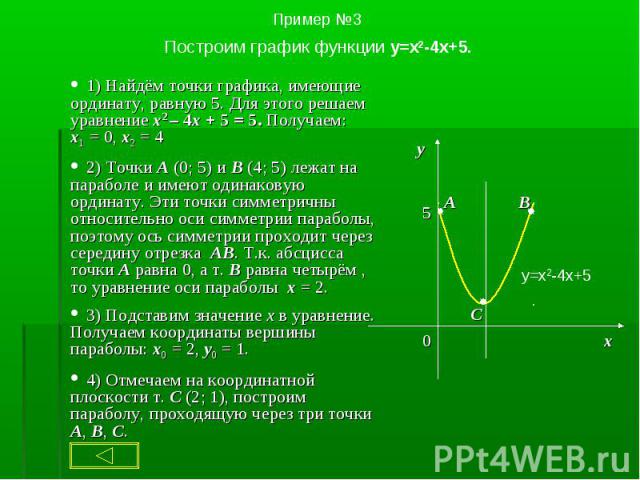
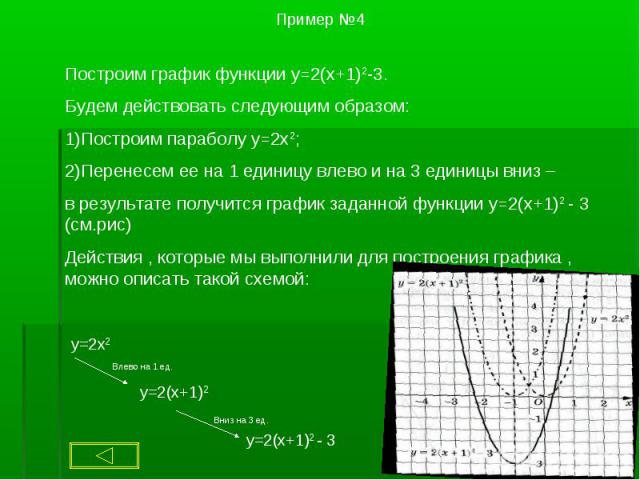
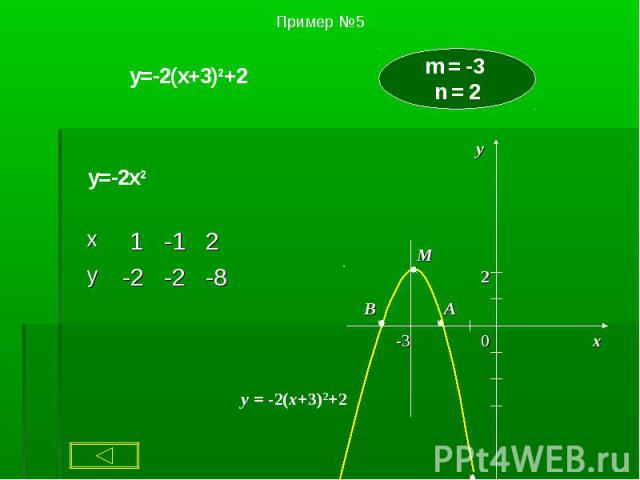
1. Чтобы построить график функции y = ax2 + g , нужно перенести параболу y = ax2 вдоль оси на g единиц вверх, если g > 0, или на | g | единиц вниз, если g < 0. При этом вершина параболы окажется в точке (0; g). 1. Чтобы построить график функции y = ax2 + g , нужно перенести параболу y = ax2 вдоль оси на g единиц вверх, если g > 0, или на | g | единиц вниз, если g < 0. При этом вершина параболы окажется в точке (0; g). 2. Чтобы построить график функции y = a(x + p)2, нужно перенести параболу y = ax2 вдоль оси x на p единиц влево, если p > 0, или на | p | единиц вправо, если p < 0.При этом вершина параболы окажется в точке (- p ; 0). 3. Чтобы построить график функции y = a(x + p )2 + g, нужно перенести параболу y = ax2 вдоль оси x на p единиц влево, если p >0, или на | p | единиц вправо, если p < 0 и вдоль оси y на g единиц вверх, если g > 0, или на | g | единиц вниз, если g < 0. При этом вершина параболы окажется в точке (- p ; g ).