Презентация на тему: Квадратичная функция.

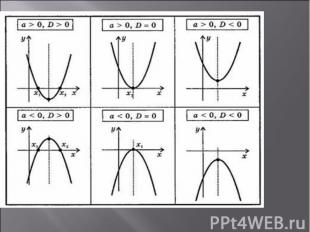
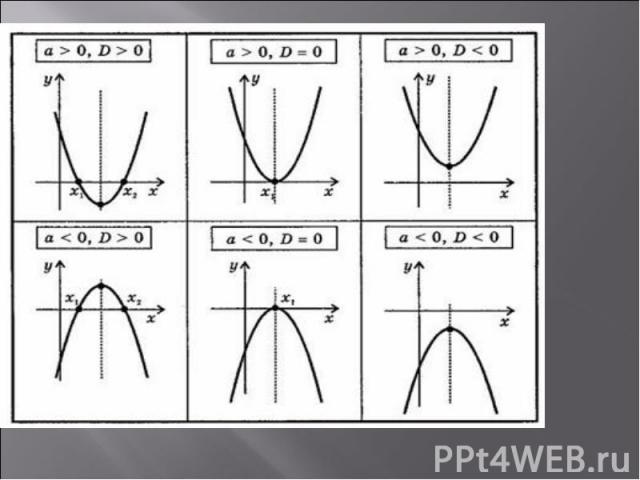
Квадратичной функцией называется функция, которую можно записать формулой вида y=ax2+bx+c, где x – независимая переменная, a, b и c – некоторые числа, причем a≠0. Графиком квадратичной функции является парабола.

Парабола - от греческого «пара» - рядом и «баллейн» - бросать. Параболой называется кривая, точки которой одинаково удалены от некоторой точки, называемой фокусом, и от некоторой прямой, называемой директрисой параболы.

Парабола симметрична относительно прямой проходящей через её вершину и направленной вдоль ветвей параболы. Ось симметрии пересекает параболу только в её вершине. Парабола имеет только одну вершину. Парабола бесконечна.

1.Если х=0, то у=0, т.е. парабола имеет с осями координат общую точку (0; 0)-начало координат. 1.Если х=0, то у=0, т.е. парабола имеет с осями координат общую точку (0; 0)-начало координат. 2. Если х≠0, то у>0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс. 3.Множеством значений функции - промежуток [0; +∞). 4. парабола симметрична относительно оси ординат (функция четная). 5.На промежутке [0; + ∞) функция возрастает. 6.На промежутке (-∞; 0] функция убывает. 7.Наименьшее значение функции равно 0. Наибольшего значения не существует.