Презентация на тему: лекция

Бинарные отношения. Отношения эквивалентности и разбиения. Отношения частичного порядка. Ирина Борисовна Просвирнина Бинарные отношения и их свойства Отношения эквивалентности Разбиения Отношения частичного порядка Диаграммы Хассе Алгоритм топологической сортировки

Отношения Декартовым произведением множеств и является множество Элементы множества называются упорядоченными парами.

Отношения Определение 1 Бинарным отношением между множествами и называется подмножество декартова произведения . Если упорядоченная пара принадлежит отношению , то пишут и говорят, что находится в отношении с . В том случае, когда , мы говорим просто об отношении на .

Отношения Пример 1 Выписать упорядоченные пары, принадлежащие следующим бинарным отношениям между множествами и }: Решение

Отношения Пример 2 Множество делитель определяет отношение на множестве Найдите все упорядоченные пары, принадлежащие . Решение

Отношения Имеется удобный способ перечисления упорядоченных пар, принадлежащих данному отношению. Он основан на понятии ориентированно графа.

Отношения Пусть и – два конечных множества и пусть – бинарное отношение между этими множествами. Изобразим элементы множеств и точками на плоскости. Для каждой упорядоченной пары отношения нарисуем стрелку, соединяющую точки, представляющие первую и вторую компоненты пары, соответственно. Такой объект называется ориентированным графом или орграфом. Точки, изображающие элементы множеств, принято называть вершинами орграфа.

Пример 3 Рассмотрим отношение между множествами и из примера 1, b): . Соответствующий ориентированный граф показан на рисунке. 1 2 3 4 5 6 7

Отношения Для иллюстрации отношения на отдельном множестве чертят орграф, чьи вершины соответствуют одному лишь множеству , а стрелки, как обычно, соединяют элементы упорядоченных пар, находящихся в данном отношении.

Отношения Свойства отношений Ограничимся изучением бинарных отношений, заданных на одном множестве и рассмотрим некоторый набор их свойств.

Отношения Определение 2 Отношение на множестве рефлексивно, если для всех из . В терминах упорядоченных пар данное отношение рефлексивно, если принадлежит для всех возможных значений .

Отношения У ориентированного графа, изображающего рефлексивное отношение, каждая вершина снабжена петлей, то есть стрелкой, начинающейся и заканчивающейся в одной и той же вершине.

Отношения Определение 3 Отношение на множестве симметрично, если из следует для всех и из . В терминах упорядоченных пар данное отношение симметрично, если из того, что принадлежит следует, что принадлежит для всех возможных значений и .

Отношения Орграф симметричного отношения вместе с каждой стрелкой из вершины в вершину имеет стрелку, направленную в обратную сторону: из в .

Отношения Определение 4 Отношение на множестве антисимметрично, если из и следует, что для всех и из . В терминах упорядоченных пар данное отношение антисимметрично, если из того, что принадлежит и принадлежит , следует, что для всех возможных значений и.

Отношения Если отношение антисимметрично, то в соответствующем орграфе при наличии стрелки из вершины в несовпадающую с ней вершину , стрелка из в будет обязательно отсутствовать.

Отношения Определение 5 Отношение на множестве транзитивно, если из того, что и следует, что для всех и из . В терминах упорядоченных пар данное отношение транзитивно, если из того, что принадлежит и принадлежит следует, что принадлежит для всех возможных значений и .

Отношения Орграф транзитивного отношения устроен так, что вместе со стрелками из вершины в вершину и из вершины в вершину , у него будет стрелка и из вершины в вершину .

Отношения Пример 5 Что можно сказать о свойствах рефлексивности, симметричности, антисимметричности и транзитивности следующих отношений: « делит » на множестве натуральных чисел; « не равно » на множестве целых чисел; «возраст совпадает с возрастом » на множестве всех людей?

Отношение эквивалентности Определение 1 Отношение на множестве называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Отношения эквивалентности играют важную роль во всех разделах математики!

Отношение эквивалентности Определение 2 Два элемента и называют эквивалентными и пишут , если находится в отношении эквивалентности с .

Примеры отношений эквивалентности Пример 1 Пусть – отношение на множестве целых чисел , определенное следующим образом: или . – отношение эквивалентности, так как оно рефлексивно, симметрично и транзитивно.

Примеры отношений эквивалентности Пример 2 Пусть – отношение на множестве вещественных чисел , определенное следующим образом: является целым числом. – отношение эквивалентности, так как оно рефлексивно, симметрично и транзитивно.

Примеры отношений эквивалентности Пример 3 Пусть – целое число, большее Пусть . – отношение эквивалентности на , так как оно рефлексивно: , симметрично: ), транзитивно:

Примеры отношений эквивалентности Пример 4 Пусть – отношение на множестве строк, составленных из букв английского алфавита, определенное следующим образом: , где – длина строки . – отношение эквивалентности, так как оно рефлексивно, симметрично и транзитивно.

Примеры отношений эквивалентности Пример 5 Пусть – натуральное число и пусть – множество строк, составленных из символов некоторого алфавита . Пусть – отношение на , определенное следующим образом: , или и состоят по крайней мере из символов, причем первые символов в строках и совпадают. – отношение эквивалентности, так как оно рефлексивно, симметрично и транзитивно.

«Антипримеры» отношений эквивалентности Пример 6 Пусть – отношение «делит» на множестве натуральных чисел . Отношение не является отношением эквивалентности, так как оно не симметрично: 2 , но 2.

«Антипримеры» отношений эквивалентности Пример 7 Пусть – отношение на множестве вещественных чисел , определенное следующим образом: не является отношением эквивалентности, так как оно не транзитивно:

Классы эквивалентности Определение 3 Пусть – отношение эквивалентности на множестве и пусть – элемент множества . Множество всех элементов из , эквивалентных элементу , называется классом эквивалентности элемента . Класс эквивалентности элемента относительно обозначается через или через , если из контекста ясно, о каком отношении идет речь. Если , то называется представителем этого класса эквивалентности.

Примеры классов эквивалентности Пример 8 Пусть – отношение на множестве целых чисел , определенное следующим образом: или . Найти . Решение Например, , , .

Примеры отношений эквивалентности Пример 9 Найти классы эквивалентности чисел и для отношения сравнимости по модулю . Решение

Примеры отношений эквивалентности Пример 10 Построить класс эквивалентности строки относительно отношения на множестве всех битовых строк. Решение

Классы эквивалентности и разбиения Теорема 1 Пусть – отношение эквивалентности на множестве . Следующие утверждения для элементов и из множества равносильны: ,

? Доказательство Пусть симметрично , , транзитивно Итак, Аналогично доказывается, что .

? Доказательство Пусть , так как по рефлексивности отношения .

? Доказательство Предположим, что существует элемент со свойством: . ∧ ∧

Классы эквивалентности и разбиения Из теоремы следует, что классы эквивалентности относительно отношения эквивалентности непустые, попарно не пересекаются и в объединении дают все множество . Другими словами классы эквивалентности образуют разбиение множества в смысле следующего определения.

Классы эквивалентности и разбиения Определение 4 Разбиением множества называется набор непустых, попарно непересекающихся подмножеств множества , объединение которых совпадает с .

Примеры разбиений Пример 11 Построить разбиение, соответствующее отношению сравнимости по модулю на множестве целых чисел . Решение Разбиение множества целых чисел состоит из четырех классов вычетов:

Примеры разбиений Пример 12 Построить разбиение, соответствующее отношению эквивалентности а множестве всех битовых строк. Решение Разбиение множества всех битовых строк состоит из восьми классов эквивалентности: , .

Отношение частичного порядка Определение 5 Отношение на множестве называется отношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно. Множество , на котором задано отношение частичного порядка , называется частично упорядоченным множеством и обозначается .

Примеры частично упорядоченных множеств Пример 1 Отношение «больше или равно» на множестве целых чисел является отношением частичного порядка.

Примеры частично упорядоченных множеств Пример 2 Отношение «делит» на множестве натуральных чисел является отношением частичного порядка.

Примеры частично упорядоченных множеств Пример 3 Отношение «содержится в» на множестве всех подмножеств множества является отношением частичного порядка.

«Антипример» частично упорядоченного множества Пример 4 Отношение « старше », определенное на множестве всех людей, не является отношением частичного порядка. Действительно, это отношение не является рефлексивным.

Отношение частичного порядка Определение 6 Пусть – частично упорядоченное множество. Два элемента и из называются сравнимыми, если или .

Отношение частичного порядка Определение 7 Если – частично упорядоченное множество, любые два элемента которого сравнимы, то называется линейно упорядоченным множеством или цепью, а отношение называется линейным порядком.

Пример линейно упорядоченного множества Пример 5 Частично упорядоченное множество является цепью.

«Антипример» линейно упорядоченного множества Пример 6 Частично упорядоченное множество не является цепью, так как и несравнимы.

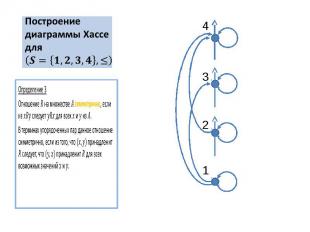
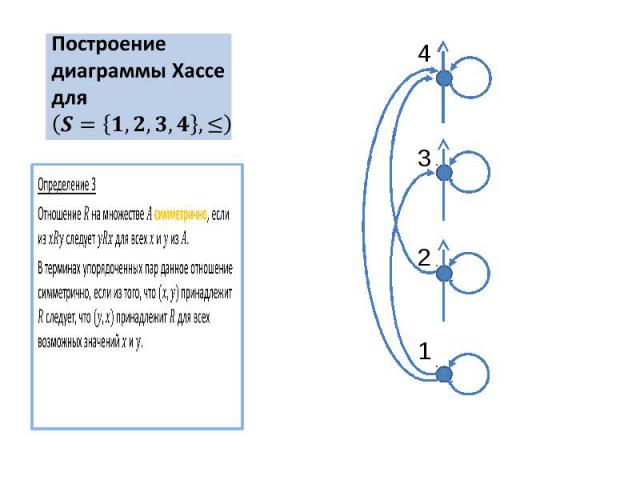
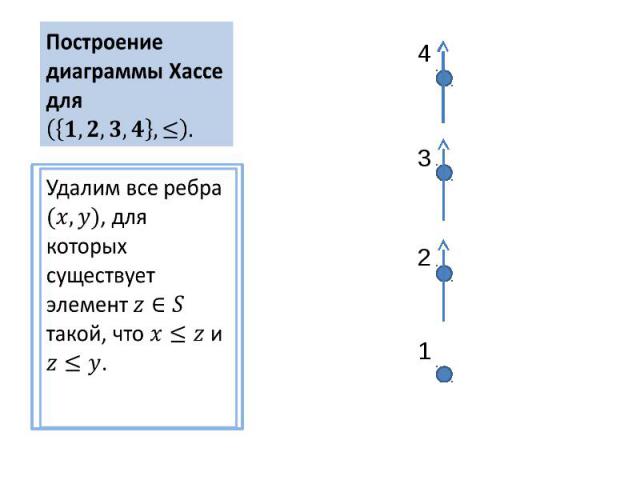
Построение диаграммы Хассе для

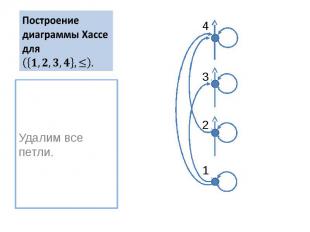
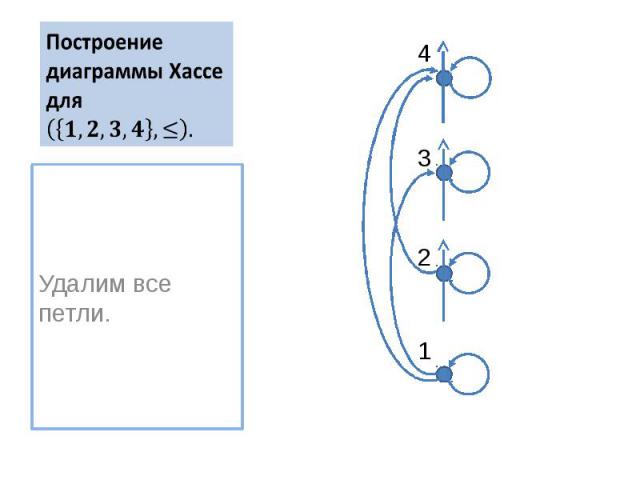
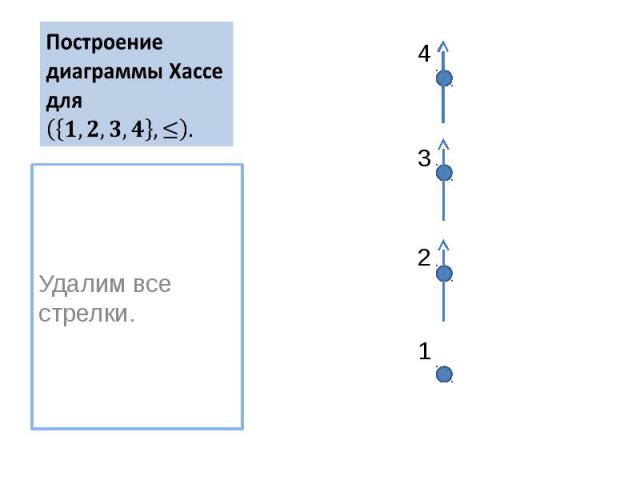
Построение диаграммы Хассе для

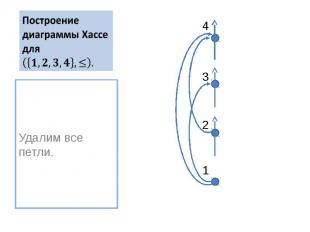
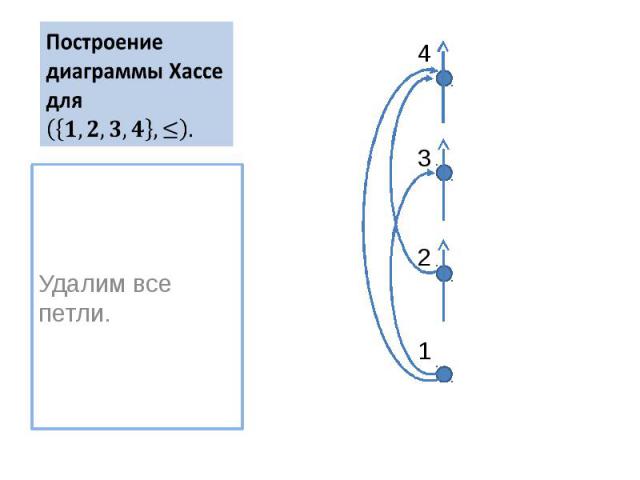
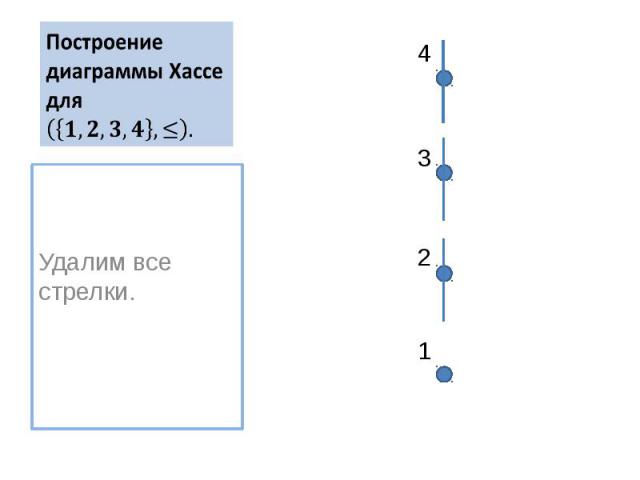
Построение диаграммы Хассе для

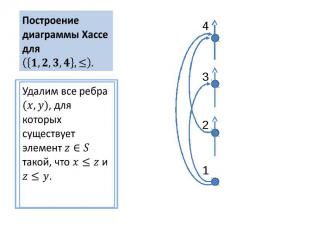
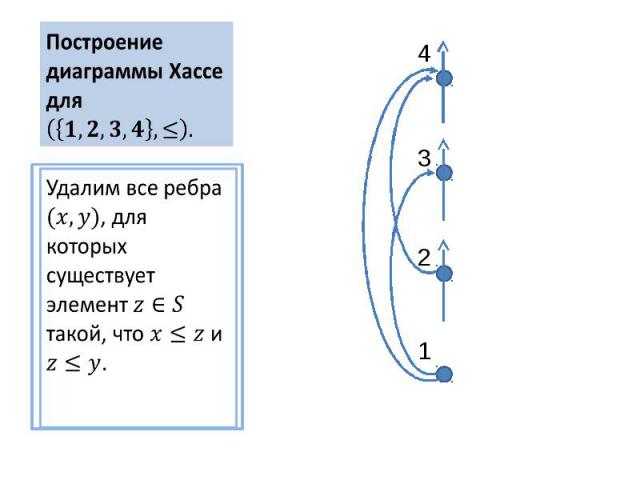
Построение диаграммы Хассе для

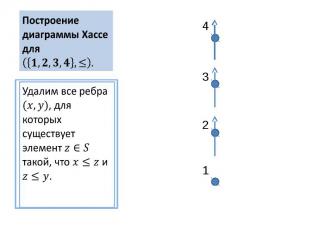
Построение диаграммы Хассе для

Построение диаграммы Хассе для

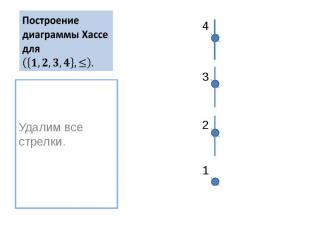
Построение диаграммы Хассе для

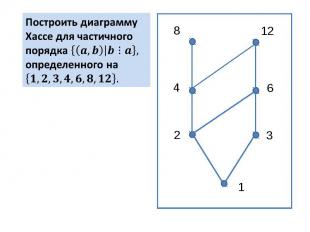
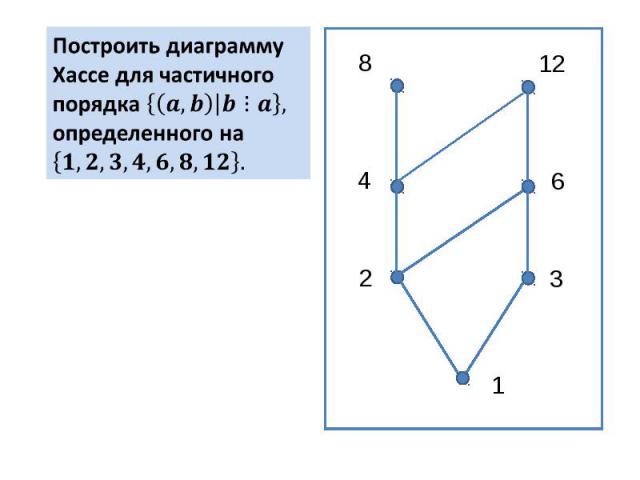
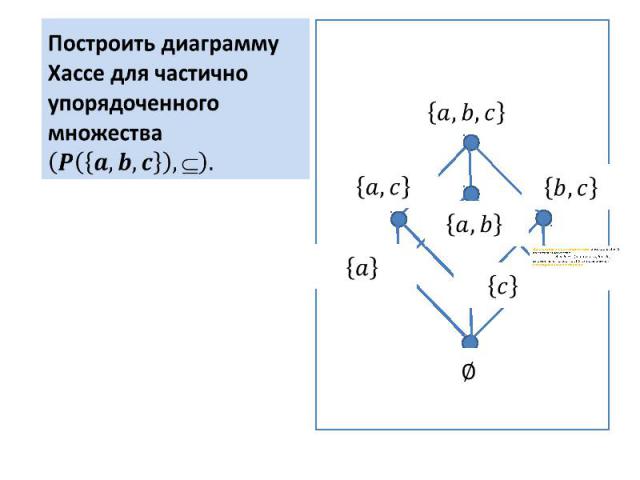
Построить диаграмму Хассе для частичного порядка определенного на

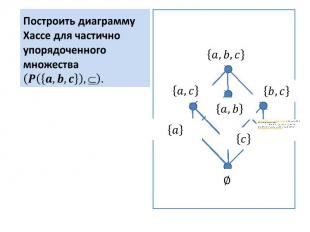
Построить диаграмму Хассе для частично упорядоченного множества

Максимальные и минимальные элементы Определение 8 Пусть – частично упорядоченное множество. Элемент из называется максимальным, если не существует элемента со свойством: . Элемент из называется минимальным, если не существует элемента со свойством: .

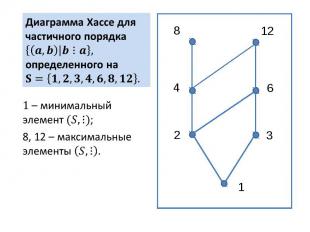
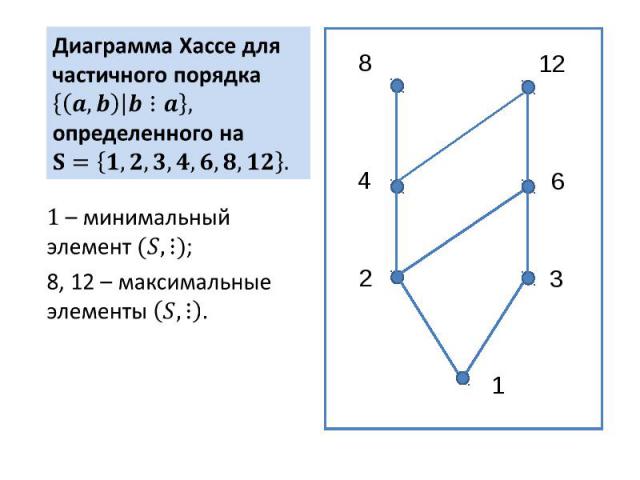
Диаграмма Хассе для частичного порядка определенного на

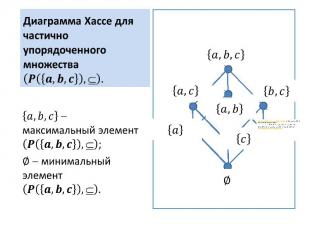
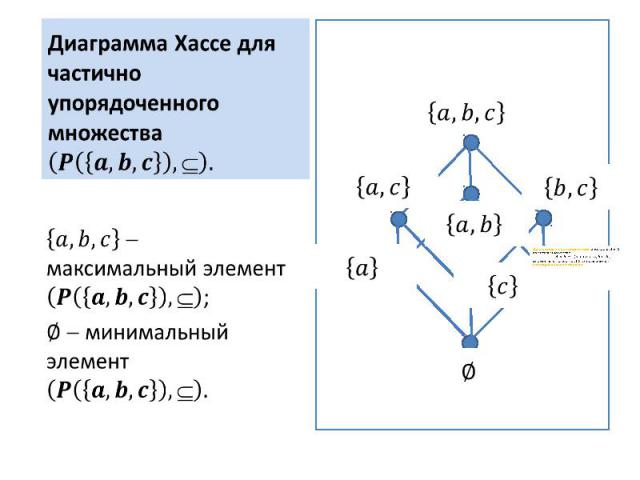
Диаграмма Хассе для частично упорядоченного множества

Топологическая сортировка Предположим, что разрабатывается проект, состоящий из 20 различных заданий. Выполнение части заданий проекта может быть начато только после того, как другие задания проекта будут полностью завершены. В какой очередности должны выполняться задания проекта? Зададим на множестве всех заданий проекта частичный порядок, положив для заданий и : не может быть начато, пока не завершено

Топологическая сортировка Определение 9 Линейный порядок называется согласованным с частичным порядком , если из того, что следует, что . Построение линейного порядка, согласованного с данным частичным порядком, называется топологической сортировкой.

Топологическая сортировка Лемма Любое конечное частично упорядоченное множество имеет хотя бы один минимальный элемент. Доказательство Выберем в множестве элемент . Если не минимальный, то найдется такой элемент в , что . Если не минимальный, то найдется такой элемент в , что . Продолжим этот процесс. Так как – конечное множество, то процесс должен закончиться построением минимального элемента множества .

Алгоритм топологической сортировки Пусть – конечное частично упорядоченное множество. Выберем в минимальный элемент . Он существует по лемме. – тоже конечное частично упорядоченное множество. Если , то выберем в частично упорядоченном множестве минимальный элемент . Он существует по лемме. Если , то выберем в частично упорядоченном множестве минимальный элемент . Продолжим этот процесс, выбрав в минимальный элемент Так как – конечное множество, процесс должен закончиться.

Алгоритм топологической сортировки Итак, для частично упорядоченного множества построен линейный порядок : Этот линейный порядок согласован с исходным частичным порядком.

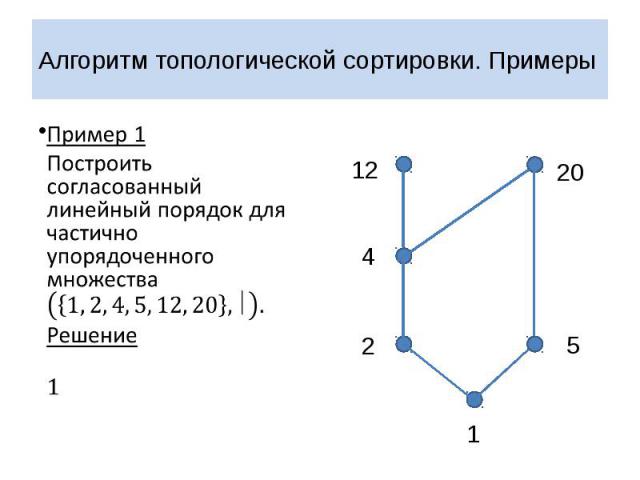
Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение

Алгоритм топологической сортировки. Примеры Пример 1 Построить согласованный линейный порядок для частично упорядоченного множества Решение 12

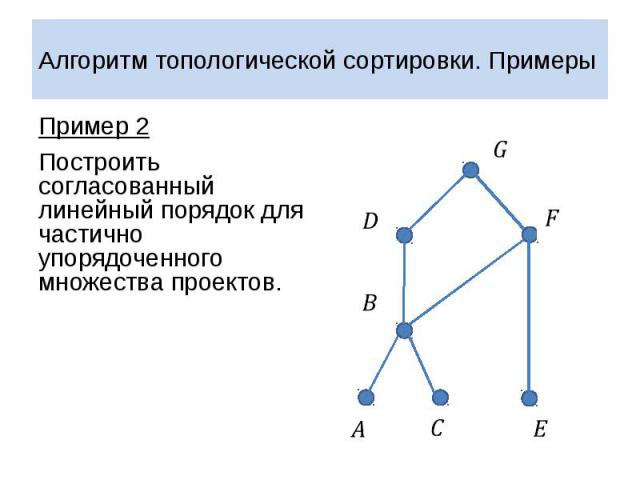
Алгоритм топологической сортировки. Примеры Пример 2 Проект развития компьютерной компании предполагает выполнение семи этапов. Выполнение некоторых этапов проекта развития может быть начато только после того, как другие этапы проекта будут полностью завершены. В какой очередности должны выполняться этапы проекта развития компании? Зададим на множестве всех этапов проекта частичный порядок, положив для этапов и : не может быть начат, пока не завершен

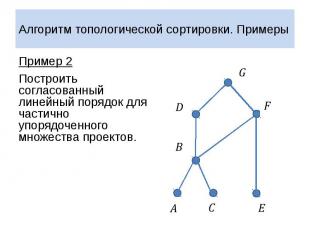
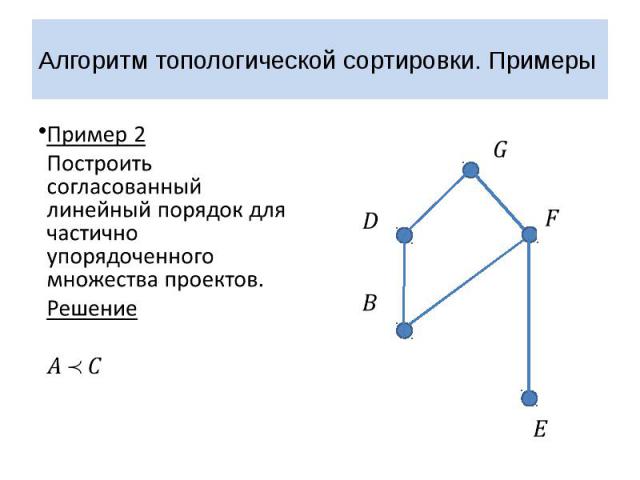
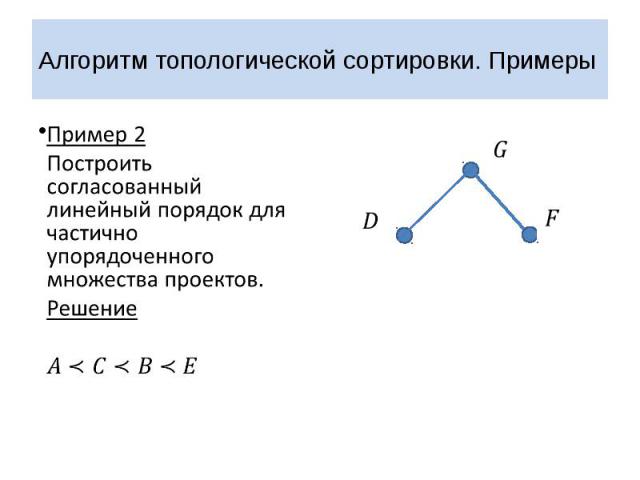
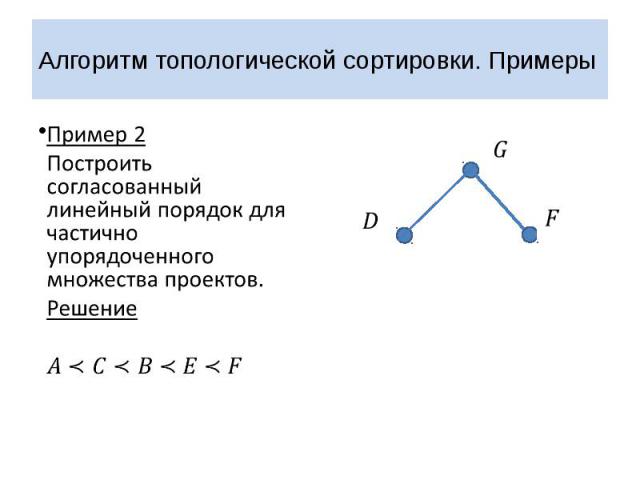
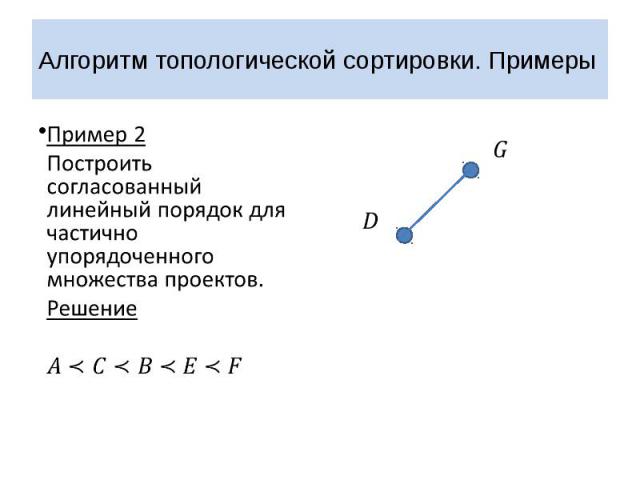
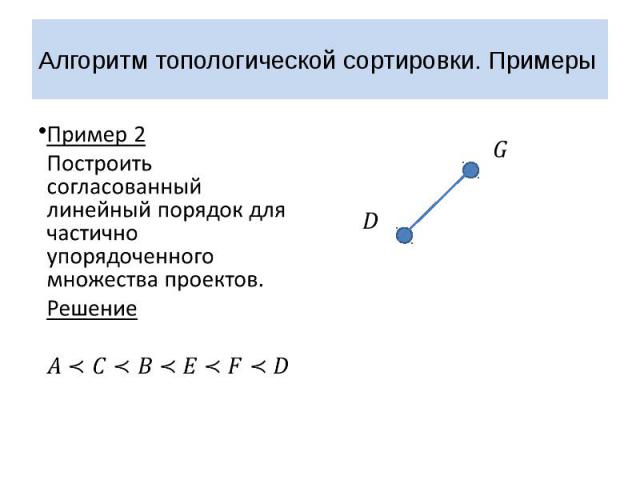
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов.

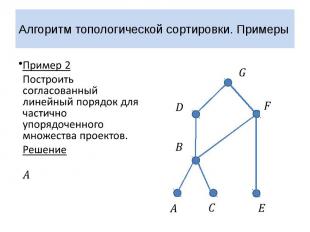
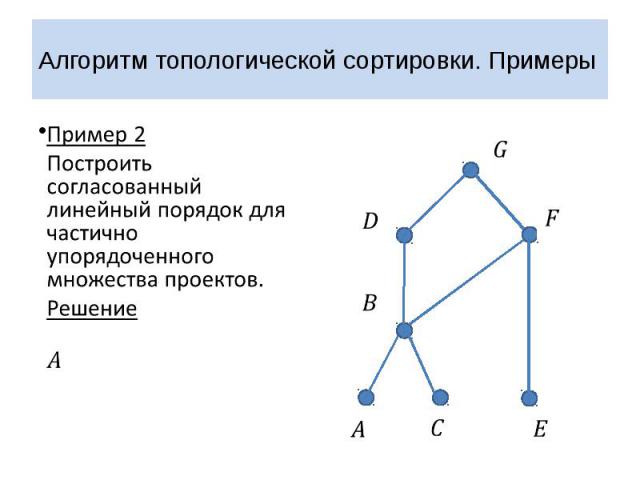
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

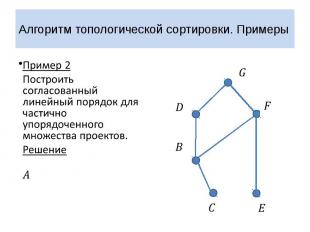
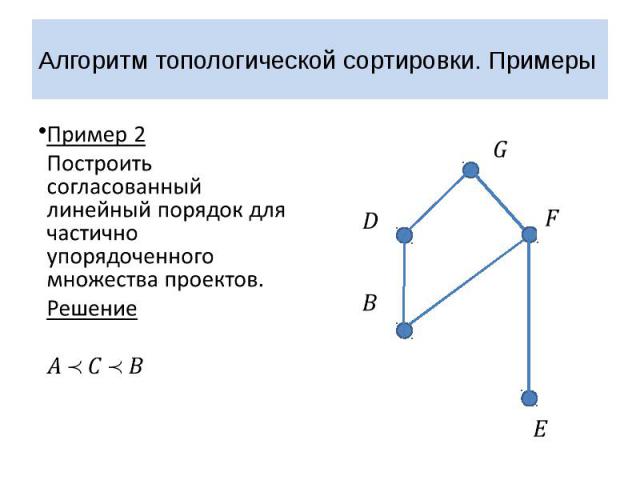
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

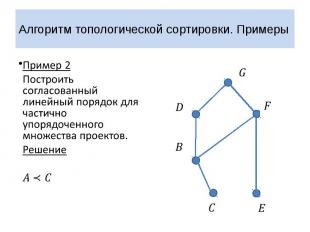
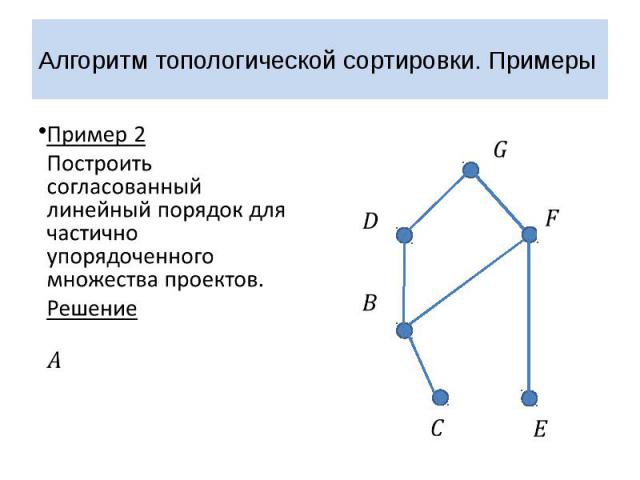
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

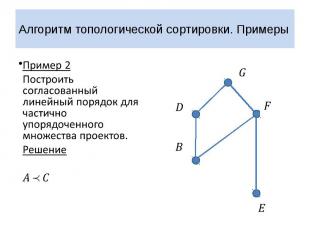
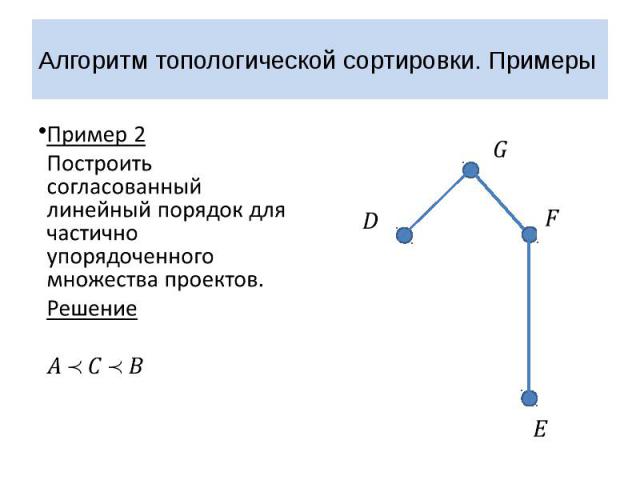
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

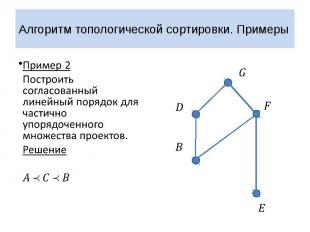
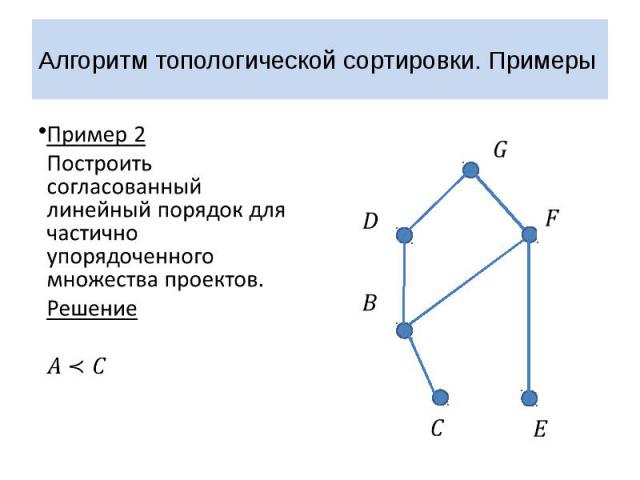
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

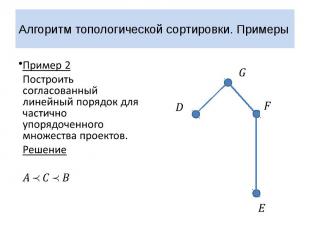
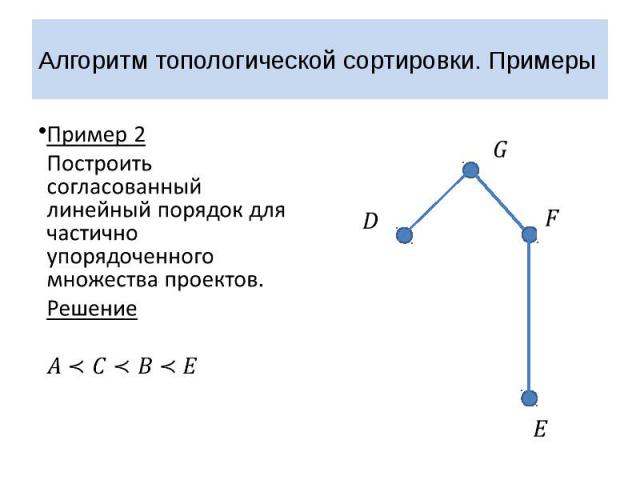
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

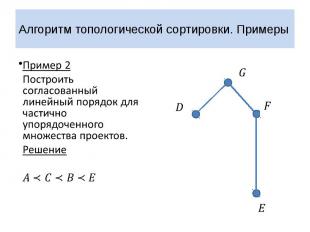
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

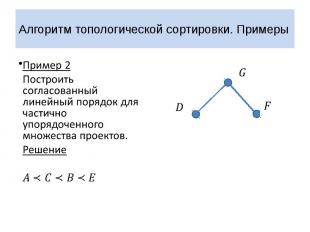
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

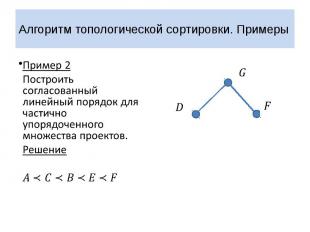
Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение

Алгоритм топологической сортировки. Примеры Пример 2 Построить согласованный линейный порядок для частично упорядоченного множества проектов. Решение