Презентация на тему: Действительные числа

АЛГЕБРА и начала анализа 10 классШ.А.Алимов, ю.м.колягин и др.15 изд. М.: Просвещение, 2007 Глава I. Действительные числаУрок 2 «Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами».И. Ньютон Учитель математики Пивоваренок Н.Н.ГОУ Школа №247

иметь понятия об: иррациональных числах; множестве действительных чисел; модуле действительного числа; уметь выполнять : вычисления с иррациональными выражениями; сравнивать числовые значения иррациональных выражений §2 Действительные числа

1. Необходимость дальнейшего расширения множества чисел связана в основном с двумя причинами: 1)Рациональных чисел недостаточно для выражения результатов измерений (длина диагонали квадрата со стороной 1) 2) Такие числовые выражения не являются рациональными числами иррациональным числом называется бесконечная десятичная непериодическая дробь

Объединение множества рациональных чисел и множества иррациональных чисел (бесконечных десятичных непериодических дробей) даёт множество R действительных чисел Действительным числом называется бесконечная десятичная дробь, т.е. дробь вида + а0,а1а2а3… или - а0,а1а2а3… , где а0 - целое неотрицательное число, а каждая из букв а1,а2,а3,… - одна из десяти цифр: 0,1,2,3,4,5,6,7,8,9 1) π = 3,1415… а0 = 3 а1=1 а2= 4 а3=1 а4=5 …2)- √234 = - 15,297058… а0 = 15 а1=2 а2= 9 а3=7 а4=0 …3)37,19 а0 = 37 а1=1 а2= 9 аn=0 при n≥3 Действительное число может быть положительным, отрицательным или равным нулю.

2. Арифметические операции над действительными числами обычно заменяются операциями над их приближениями. Числа 3; 3,1; 3,15 и т.д. являются последовательными приближениями значения суммы

3. Все основные действия над рациональными числами сохраняются и для действительных чисел

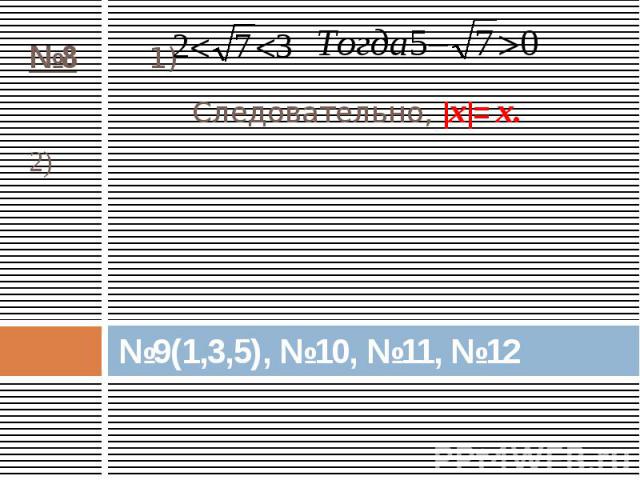
№8 1) Следовательно, |х|= х.2) №9(1,3,5), №10, №11, №12

№10, №11, №12№9(1,3,5)

№11, №12№10

§2, разобрать задачу 3 (стр.6);№9 (2, 4, 6),№11 (2),№93 ,№5 (2). Домашнее задание

Итоги урока №2Глава1 , §2