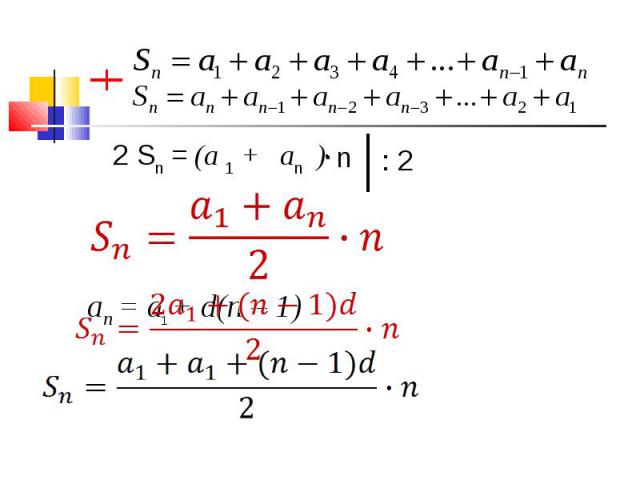Презентация на тему: Формула суммы первых n членов арифметической прогрессии

Формула суммы первых n членов арифметической прогрессии Методическая разработка Т.С. Панкратовой, учителяМАОУ «СОШ № 127» г. Перми

Карл Гаусс(1777 – 1855) выдающийся немецкий математик, астроном и физик, считается одним из величайших математиков всех времён. «Король математики»Математический талант Гаусса проявился ещё в детстве. По легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс быстро вычислил.

Найти сумму первых 100 натуральных чисел S – суммаS= 1 + 2 +3+…+98+99+100S=100+99+98+…+ 3 + 2 + 12S=101*100 |:2

Найти сумму первых 10 натуральных чисел. 1+2+3+4+5+6+7+8+9+10= = 55

Sn – сумма первых n членов арифметической прогрессии

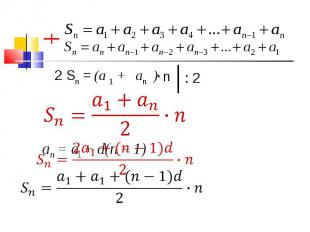
Найдите сумму первых сорока членов последовательности, заданной формулой: Данная последовательность вида a =k n + b, значит, это арифметическая прогрессия

Найдём сумму первых тридцати членов арифметической прогрессии 4; 5,5;…

Задача 19. ГИА – 2011г. Найдите сумму всех натуральных чисел, не превосходящих 150, которые не делятся на 5.

Найдите сумму всех натуральных чисел, кратных 3,заключенных в промежутке от 100 до 200.Формула, задающая натуральные числа кратные 3:

Найдите сумму натуральных чисел больших 50, но меньших150 и не кратных 5?

Последовательность чисел: 55; 60; 65; … ; 145 – арифметическаяпрогрессия со знаменателем 5.

Укажите наибольшее число членов арифметической прогрессии – 42; – 38; – 34; …, сумма которых меньше 150.