Презентация на тему: Метод рационализации

Метод рационализации Работу выполнили: Белозерова О.М. Шарикова И.Е. г.Георгиевск

Введение Решение неравенств - важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные неравенства, поэтому мы решили рассмотреть один из способов решения неравенств – метод рационализации. В школьной программе он не изучается, но его применение значительно облегчает решение задания С3 ЕГЭ, в частности логарифмических и показательных неравенств.

Теоретическое обоснование метода Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:

Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности. Уже при данных квадратичных функциях решение совокупности может потребовать много времени. Можно предложить альтернативный, менее трудоемкий метод решения этого стандартного неравенства. Это метод рационализации неравенств, известный в математической литературе под названием декомпозиции. Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x), при котором неравенство G(x) >0 равносильно неравенству F(x) >0 в области определения выражения F(x).

Сведение логарифмического неравенства к системерациональных неравенств Рассмотрим логарифмическое неравенство вида , (1)где - некоторые функцииТеорема 1. Логарифмическое неравенство равносильно следующей системе неравенств: (2)

Доказательство Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство Если , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.

Сведение показательныхнеравенств к системерациональных неравенств Теперь рассмотрим показательное неравенство вида 3) Так же, как в предыдущем пункте, - некоторые функции. И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям. В первом основание степени положительно, но меньше единицы (знак неравенства обращается), во втором случае основание степени больше единицы (знак неравенства сохраняется).Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.

Теорема 2. Показательное неравенство равносильно следующей системе неравенств: (4)

Доказательство Если , то первый множитель третьего неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство . Если , то первый множитель третьего неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство .

Выделим некоторые выражения F и соответствующие им рационализирующие выражения G, где f, g, h, p, q – выражения с переменной x (h > 0,h а – фиксированное число (a > 0, a

Доказательство Пусть loga f- loga g> 0, то есть loga f> loga g, причём a > 0, a ≠ 1, f > 0, g > 0. Если 0 < a < 1, то по свойству убывающей логарифмической функции имеем f < g. Значит, выполняется система неравенств a -1<0 f – g < 0 Откуда следует неравенство (a – 1)(f – g) > 0 верное на области определения выражения F = loga f- logag. Если a > 1, то f > g. Следовательно, имеет место неравенство (a – 1)(f – g)> 0. Обратно, если выполняется неравенство (a – 1)(f – g)> 0 на области допустимых значений (a > 0, a ≠ 1, f > 0, g > 0), то оно на этой области равносильно совокупности двух систем. a – 1<0 a – 1 > 0 f – g < 0 f – g > 0Из каждой системы следует неравенство loga f> loga g, то есть loga f- loga g> 0. Аналогично, рассматриваются неравенства F < 0, F ≤ 0, F ≥ 0.

Пусть некоторое число а > 0 и а ≠ 1, тогда имеем = Знак последнего выражения совпадает со знаком выражения или (h-1)(f-g) .

Так как = то, используя замены 2а и 2б, получаем, что знак последнего выражения совпадает со знаком выражения (f - 1)(g - 1)(h - 1)(g – f).

Из неравенства > 0 следует . Пусть число а > 1, тогда loga > loga или (h – g)loga h > 0. Отсюда с учётом замены 1б и условия a > 1 получаем (f – g)(a – 1)(h – 1) > 0, (f – g)(h – 1) > 0. Аналогично, доказываются неравенства F < 0, F ≤ 0, F ≥ 0. Доказательство проводится аналогично доказательству 4. Доказательство замены 6 следует из равносильности неравенств | p | > | q | и p2 > q2 ( | p | < | q | и p2 < q2).

Пример 1. Решить неравенство:Решение:

ОТВЕТ:

Пример 2. Решить неравенство:Решение:

ОТВЕТ:

Пример 3. Решить неравенство:Решение:

Пример 4. Решить неравенство:Решение:

Решите примеры Пример 5.Пример 6.Пример 7.Пример 8.

Пример 9.Пример 10.Пример 11.

Пример 5

Пример 6

Пример 7

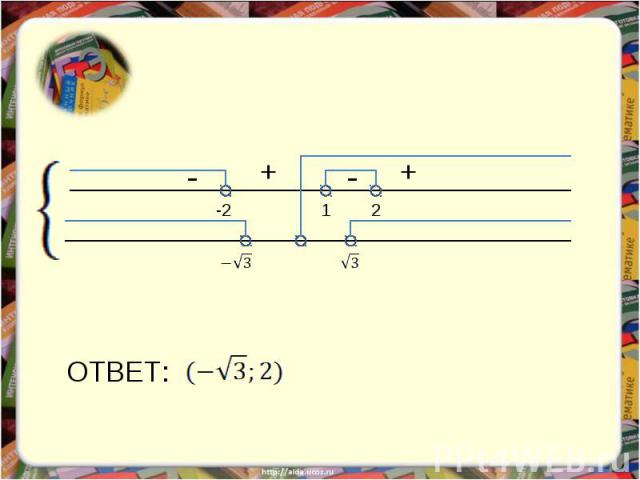
Пример 8 ОТВЕТ:

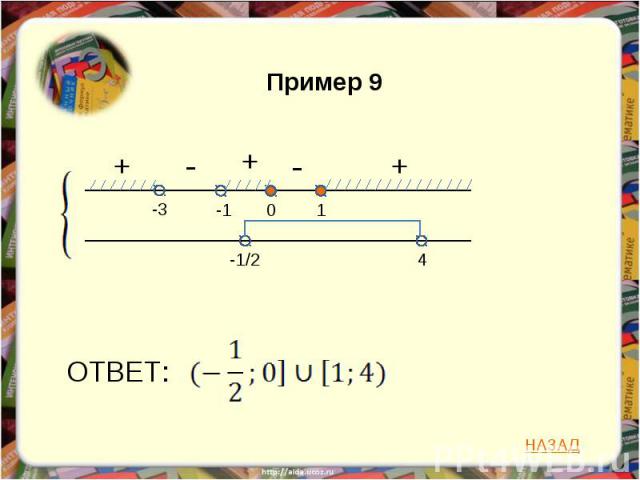
Пример 9 ОТВЕТ:

Пример 10 ОТВЕТ:

Пример 11 ОТВЕТ:

С П И С О Киспользованной литературы Корянов А. Г., Прокофьев А. А. – Методы решения неравенств с одной переменной. – 2011.Моденов В. П. – Пособие по математике. – 1972.Ткачук В.В. - Математика абитуриенту. Москва: МЦНМО, 2008.