Презентация на тему: Теорема Пифагора

Учитель математики МБОУ «Буныревская СОШ №14» Кочеткова Е.А.

1.Найдите площадь квадрата со стороной 3 см; 1,2 мм; 5\7 м; см; а см . Ответы: 9 см2; 1,44 см2; 25\49 см2; а2 см2. 2. Найдите площадь прямоугольного треугольника с катетами 3 см и 4 см; 2,2 м и 5 см; а см и в см. Ответы: 6 см2; 550 см2; 1\2 ав см2.

3. Найти высоту параллелограмма, B C если его площадь равна 40 см2, а сторона АD=8 см. A H D Выбери правильный ответ: а) 5 см; б) 10 см; в) 2 см.

Биография Пифагора Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора называют имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора).

И. Дырченко Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим — И таким простым путем К результату мы придем.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2=a2+b2 c a b

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА Пусть Т— прямоугольный треугольник с катетами а, b и гипотенузой с . Докажем, что с2=а2+Ь2 Построим квадратQ со стороной а+Ь. Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T) . Так как S(Q)=(a+b) 2 ; S(P)=c2 и S(T)=1/2(ab), то (a+b)2=c2+4*(1/2)ab или a2+b2+2ab=c2+2ab и с2=а2+Ь2. c a b b a b a b a c c c


Задача индийского ученого Бхаскара Акариа, 1114 г. На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя. Теорема Пифагора всегда имела широкое применение при решении самых разнообразных геометрических задач. Решение. 1) AB2 = AC2 + BC2, AB = 5, 2) 5 + 3 = 8 (футов) – высота тополя.

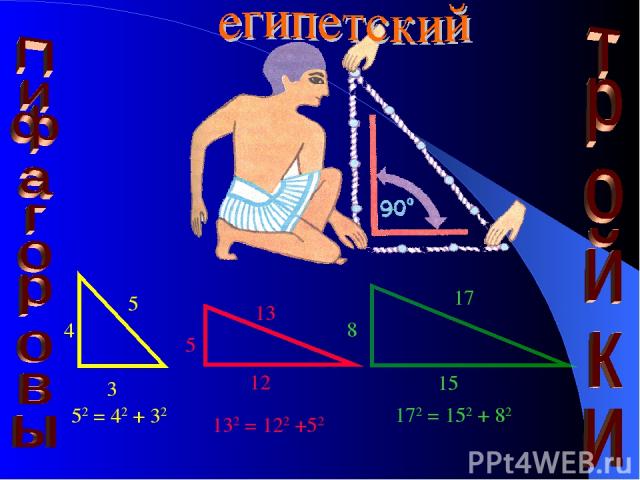
1 Пифагор родился на острове: а).Родос б)Крит в)Мадагаскар г)Самос Ответ: г 2. Теорема Пифагора гласит: a)В треугольнике квадрат гипотенузы равен квадрату катетов. б)В прямоугольном треугольнике гипотенуза равна сумме катетов. в)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. г)В прямоугольнике квадрат гипотенузы равен сумме квадратов катетов. 4. Выберите тройку пифагоровых чисел: а)2, 3 и 5 б)4, 5 и 8 в)5, 12 и 13 г)9, 11 и 14 3. Выберите верное равенство для прямоугольного треугольника: а)a2+ c2 = b2 б)a2 + b2 = c в)b2 + c2 = a2 г)a2 + b2 = c2 Ответ: г Ответ: в Ответ: в ТЕСТ