Презентация на тему: Из жизни четырёхугольников

Из жизни четырёхугольников Урок обобщения и систематизации зун

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия.» Ле Корбюзье
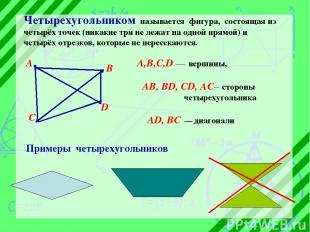
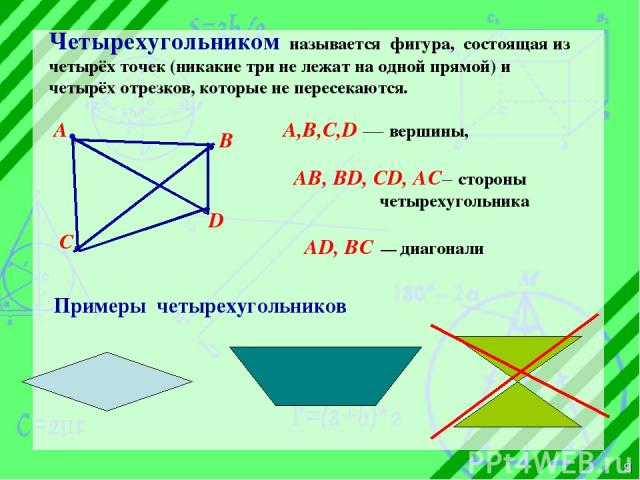
Четырехугольником называется фигура, состоящая из четырёх точек (никакие три не лежат на одной прямой) и четырёх отрезков, которые не пересекаются. С А В А,В,С,D — вершины, АВ, ВD, CD, AC– стороны четырехугольника AD, BC диагонали D в


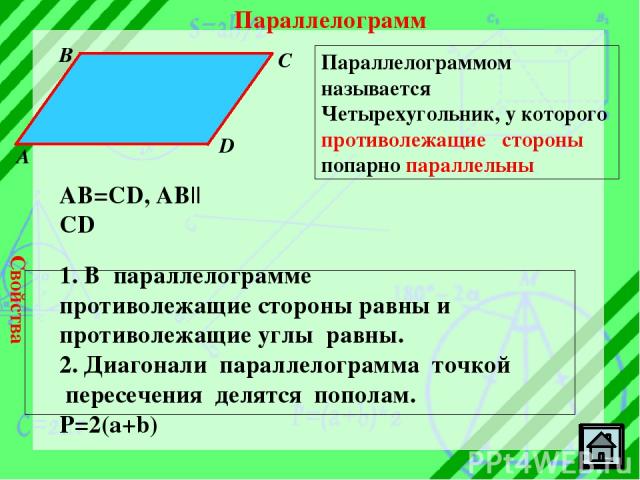
Параллелограмм Параллелограммом называется Четырехугольник, у которого противолежащие стороны попарно параллельны B C A D AB=CD, AB||CD

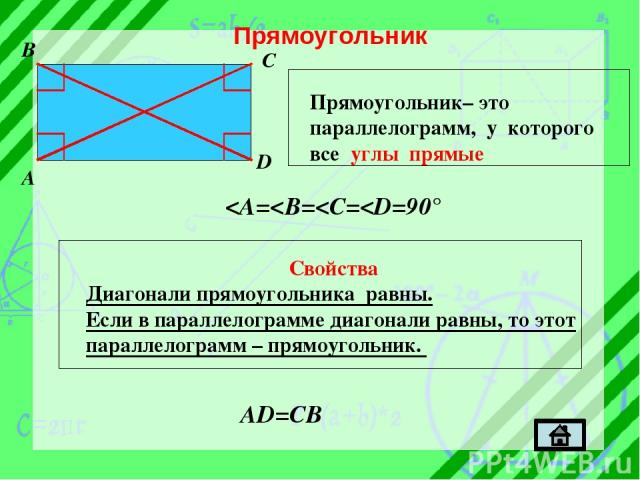
Прямоугольник B C A D Прямоугольник– это параллелограмм, у которого все углы прямые
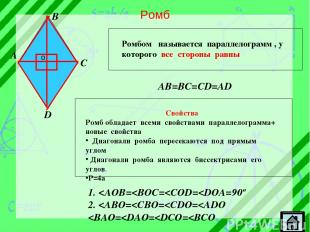
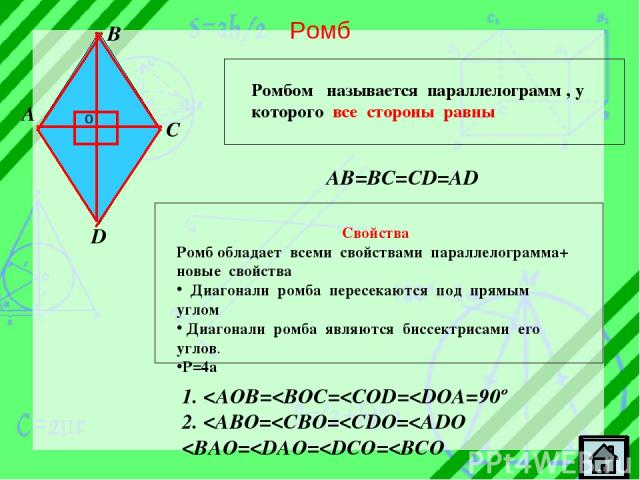
Ромб A B C D Ромбом называется параллелограмм , у которого все стороны равны AB=BC=CD=AD 1.

Квадрат A C B D Квадрат - это прямоугольник, у которого все стороны равны
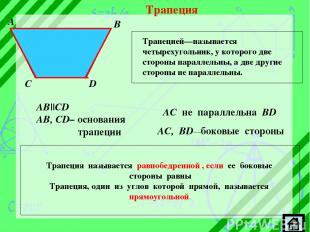
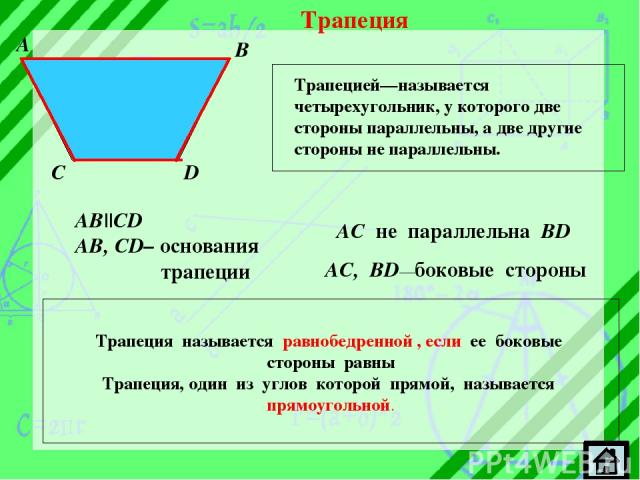
Трапеция Трапецией—называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. A B C D AB||CD AB, CD– основания трапеции AC не параллельна BD AC, BD—боковые стороны
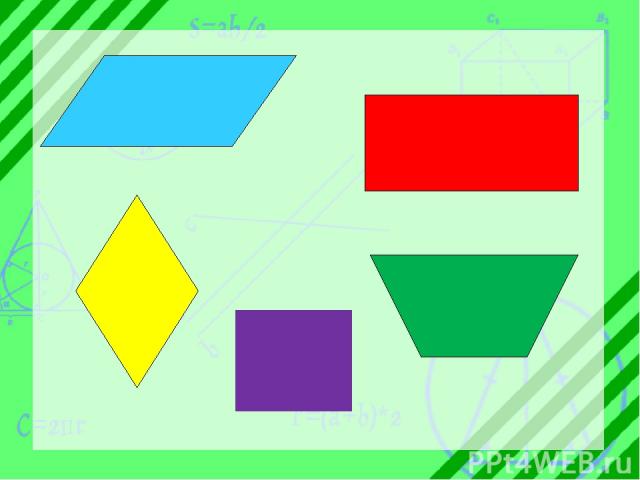
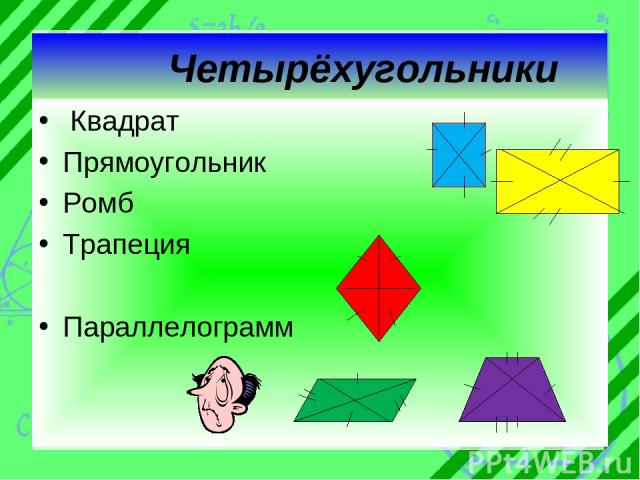
Четырёхугольники Квадрат Прямоугольник Ромб Трапеция Параллелограмм

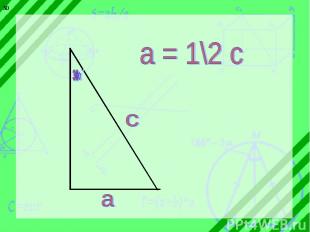
30 30 30 30 30 30
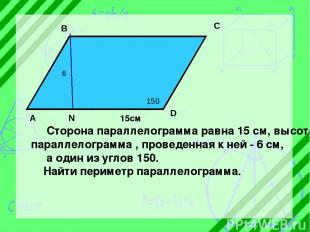
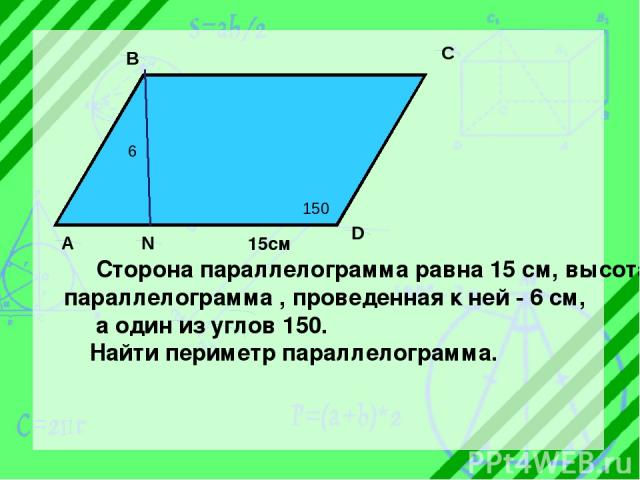
6 150 A B C D N 15см Сторона параллелограмма равна 15 см, высота параллелограмма , проведенная к ней - 6 см, а один из углов 150 . Найти периметр параллелограмма.
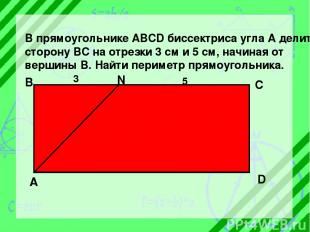
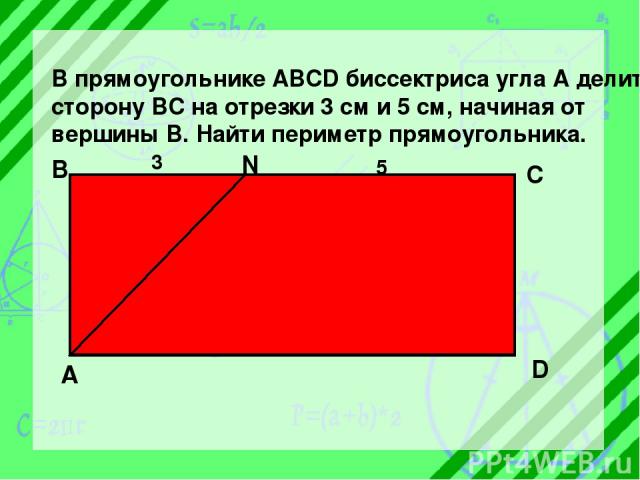
В прямоугольнике ABCD биссектриса угла А делит сторону ВС на отрезки 3 см и 5 см, начиная от вершины В. Найти периметр прямоугольника. А В N C D 3 5
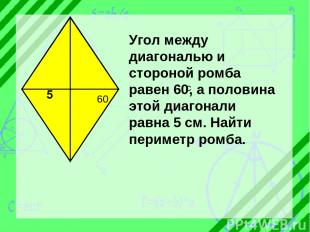
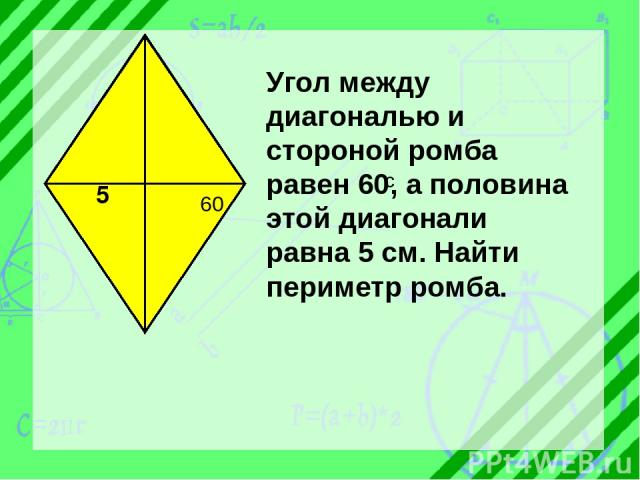
60 5 Угол между диагональю и стороной ромба равен 60 , а половина этой диагонали равна 5 см. Найти периметр ромба.

Паркетчик вырезал квадраты из дерева и проверял свою работу, сравнивая длины их сторон. Если все четыре стороны были равны, то он считал квадрат вырезанным правильно. Надежна ли такая проверка?

Другой паркетчик проверял свою работу иначе. Он мерил не стороны квадрата, а их диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат, вырезанным правильно. Прав ли он в этом случае?
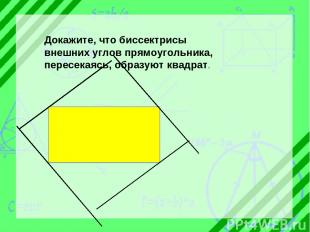
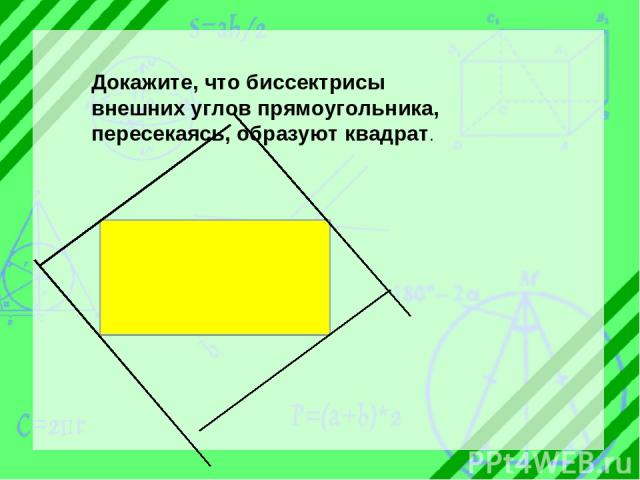
Докажите, что биссектрисы внешних углов прямоугольника, пересекаясь, образуют квадрат.


РЕШИ ЗАДАЧУ Перпендикуляр, опушенный из вершины угла A прямоугольника ABCD на не проходящую через эту вершину диагональ, делит её в отношении 1:3 считая от вершины B. Диагональ прямоугольника 8 см. найдите расстояние от точки пересечения диагоналей до A большей стороны.

ДОМАШНЕЕ ЗАДАНИЕ П.13-16(повторить) с.108 №1,2,5 Задача 1. Представьте, что в результате кораблекрушения вы попали на необитаемый остров. Чтобы где-то жить, нужно построить хижину. Для этого необходимо наметить на местности участок прямоугольной формы. У вас нет транспортира, чтобы отметить прямые углы, но есть четыре колышка и 3 веревки разной длины. С помощью этих предметов наметьте участок прямоугольной формы.