Презентация на тему: Касательная плоскость к сфере

Касательная плоскость к сфере

Цели урока: - рассмотреть теоремы о касательной плоскости к сфере; -научиться решать задачи по данной теме.

Устный опрос учащихся. Что называется сферой? Что называют диаметром сферы? Расскажите о взаимном расположении сферы и плоскости.

Изучение нового материала Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости Дано: сфера с центром в точке О и радиусом R, l-касательная плоскость, А-точка касания. Доказать:R┴ l. .О А l

Доказательство: Предположим противное: пусть R ┴ l, следовательно ОА – наклонная к плоскости l, значит, расстояние от центра, сферы до плоскости l меньше R=ОА:d< R, значит, сфера и плоскость l пересекает по окружности, что противоречит условию, что l-касательная плоскость, т.е. плоскость l и сфера имеют одну общую точку. Значит, R┴ l

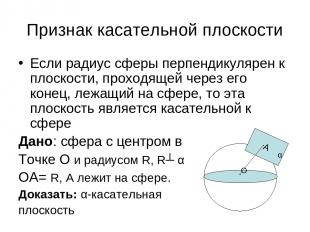
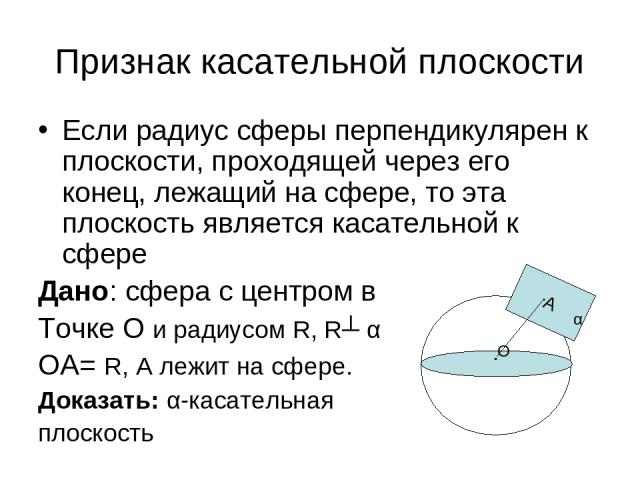
Признак касательной плоскости Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере Дано: сфера с центром в Точке О и радиусом R, R┴ α ОА= R, А лежит на сфере. Доказать: α-касательная плоскость А . О . α

Доказательство: Радиус перпендикулярен к данной плоскости R┴ α, значит, расстояние от центра сферы до плоскости равно радиусу сферы d = R, следовательно, сфера и плоскость имеют только одну общую точку, то есть данная плоскость является касательной.

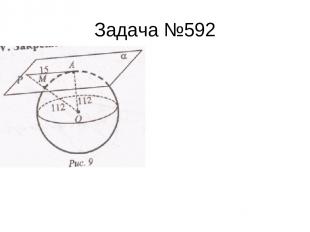
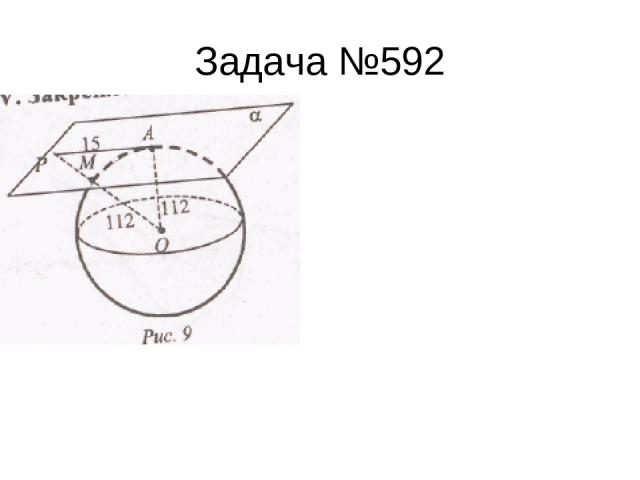
Задача №592

Подведение итогов 1.Вспомним понятие касательной плоскости к сфере. 2.Свойство касательной плоскости. 3.Признак касательной плоскости.

Домашнее задание Пп.58-61, вопросы 7-9 к главе 6,№591 Задача. Дан шар с центром в точке О, α-касательная плоскость, точка А-точка касания, точка В лежит на плоскости α, АВ=21см,ВО=29см. Найдите радиус шара