Презентация на тему: Теорема Пифагора вне школьной программы

Теорема Пифагора вне школьной программы

Существенно расширить круг геометрических задач, решаемых школьниками. Познакомить учащихся с основными этапами жизни и деятельности Пифагора. Познакомить учащихся с многообразием доказательства теоремы Пифагора. Осуществление межпредметной связи геометрии с алгеброй, географией, историей, литературой. Повышение интереса к предмету.

«Не делай никогда того, чего не знаешь, но научись всему, что нужно знать». Пифагор

Особое место в геометрии, особую роль играет прямоугольный треугольник, теорема Пифагора, соотношение между сторонами и углами в прямоугольном треугольнике. Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах" - квадрате на гипотенузе, равновеликом двум квадратам на катетах.

Причина такой популярности теоремы Пифагора триедина: это В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении.

В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Во времена же Пифагора она звучала так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».
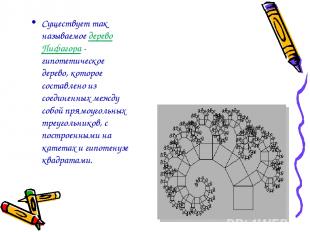
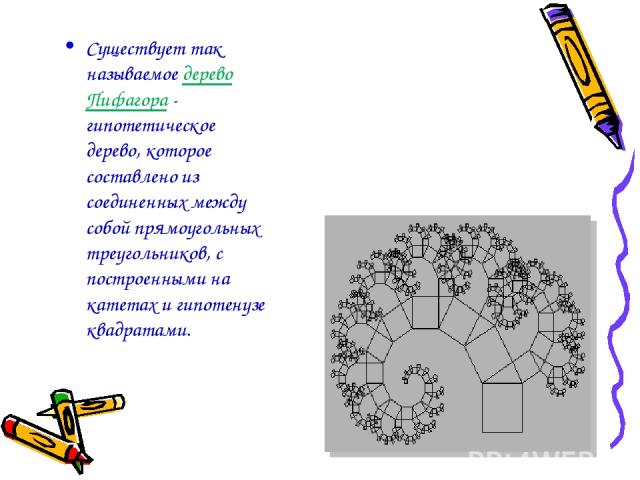
Существует так называемое дерево Пифагора - гипотетическое дерево, которое составлено из соединенных между собой прямоугольных треугольников, с построенными на катетах и гипотенузе квадратами.

Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. 3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

История открытия теоремы Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения.

О теореме Пифагора в своих работах писали многие учёные: греческий писатель-моралист Плутарх, математик 5 века Прокл и другие. Возможно, кто-то из вас читал сонет немецкого писателя - романиста Шамиссо: Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, вслед. Они не в силах свету помешать , А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.

Способы доказательства теоремы Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось "ослиным мостом" или "бегством убогих", а сама теорема - "ветряной мельницей" или "теоремой невест". Учащиеся даже рисовали карикатуры и составляли стишки вроде этого: Пифагоровы штаны Во все стороны равны.
ШАРЖИ

Доказательства, основанные на использовании понятия равновеликости фигур Древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «Смотри!». Вполне возможно, что такое же доказательство предложил и Пифагор.

Доказательства методом достроения Доказательство Леонардо да Винчи Дано: На рисунке изображена обычная Пифагорова фигура – прямоугольный треугольник ABC с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.

Доказательство: Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ. Поворот четырехугольника CBNM вокруг точки В на 90° по часовой стрелке отображает его на четырехугольник EPBA, который в свою очередь равен четырехугольнику EDFP. Теорема доказана.

Доказательства методом разложения Доказательство Перигаля Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены рядом. Надо разделить эту фигуру всего на 3(!) части, чтобы сложить из них квадрат на гипотенузе. На иллюстрации наглядно дано это разрезание.

Существуют также задачи на теорему Пифагора в стихах. Задача Бхаскари «На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?»
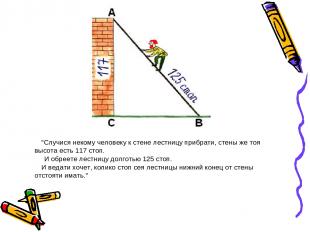
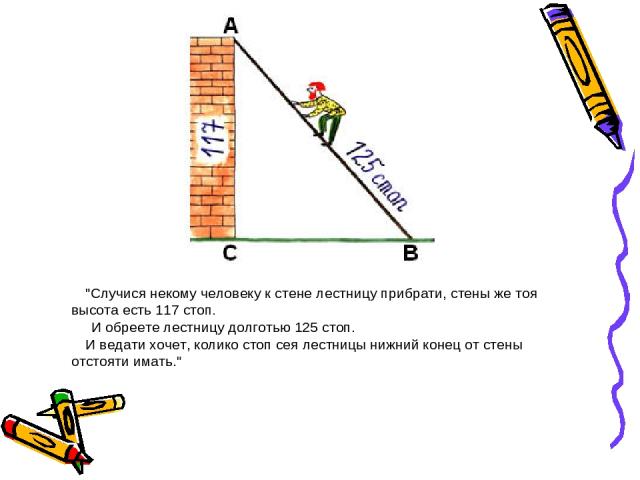
"Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."

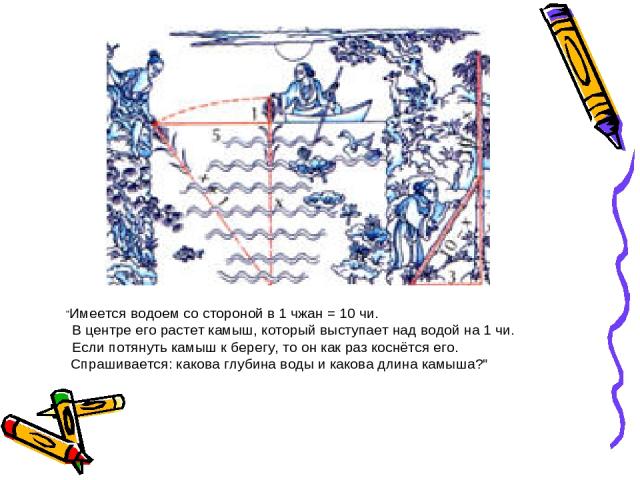
"Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?"