Презентация на тему: Способы решения квадратных уравнений

Способы решения квадратных уравнений Фестиваль педагогических идей “Открытый урок”.“Презентация к уроку” Преподаватель математики Московского суворовского военного училища Корнякова Елена Владимировна

Способы решения квадратных уравнений Нахождение корней неполных квадратных уравненийНахождение корней уравнения по формуле IНахождение корней уравнения по формуле IIНахождение корней уравнения с помощью обратной теоремы Виета Свойства коэффициентов квадратного уравнения

Неполные квадратные уравнения

Нахождение дискриминанта 2. Определение количества корней квадратного уравнения и их нахождение, в зависимости от значения D D>0 – два корня D=0 – один корень D<0 – нет корней

Формула II (коэффициент b - четный) 1. Нахождение дискриминанта 2. Определение количества корней квадратного уравнения и их нахождение, в зависимости от значения D1 D1 >0 – два корня D1=0 – один корень D1<0 – нет корней

Обратная теорема Виета Если числа m и n таковы, что их сумма равна –р, а их произведение равно q, то эти числа являются корнями уравнения x2 + px + q = 0 Пример 1.х2 + 2х – 48 = 0х1 + х2 = -2 и х1 * х2 = -48 х1 = -8; х2 = 6Ответ; -8; 6 Пример 2.х2 + 16х + 63 = 0х1 + х2 = -16 и х1 * х2 = 63х1 = -7; х2 = -9Ответ: -9; -7 Пример 3.х2 – 19х + 88 = 0х1 + х2 = 19 и х1*х2 = 88х1 = 8; х2 = 11Ответ: 8; 11

Свойства коэффициентов уравнения Если a + b + c = 0, то х1 = 1, х2 = Пример: 2х2 – 113х + 111 = 02 – 113 + 111 = 0х1 = 1; х2 = 55,5Ответ: 1; 55,5Если a – b + c = 0, то х1 = - 1, х2 = -Пример: 4х2 + 117х + 113 = 0 4 – 117 + 113 = 0х1 = - 1; х2 = - 28,25 Ответ: - 28,25; - 1

Решение уравнений по формуле I

Решение уравнений по формуле I

Решение уравнений по формуле I Ответ: нет корней

Решение уравнений по формуле II Ответ: -8; 6

Решение неполных квадратных уравнений (с = 0) 5х2 – 12х = 0х(5х – 12) = 0х1 = 0 или 5х – 12 = 0,5х = 12,х2 = 2,5.Ответ: 0; 2,5

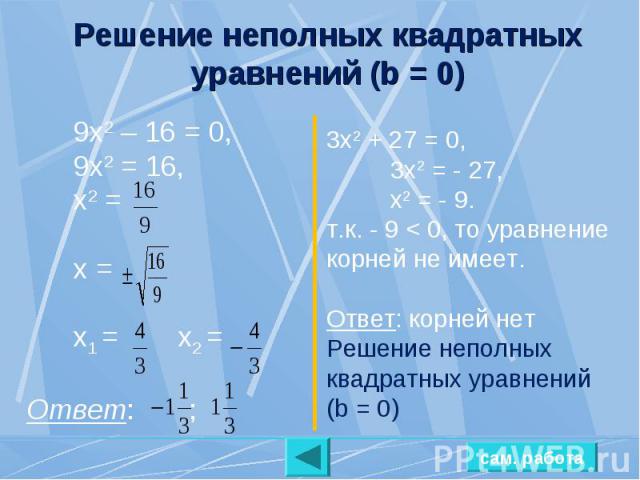
Решение неполных квадратных уравнений (b = 0) 9х2 – 16 = 0, 9х2 = 16, х2 = х = х1 = х2 =Ответ: ; 3х2 + 27 = 0,3х2 = - 27,х2 = - 9.т.к. - 9 < 0, то уравнение корней не имеет.Ответ: корней нет Решение неполных квадратных уравнений (b = 0)

Самостоятельная работа Решите уравнение: