Презентация на тему: Подготовка учащихся к городскому туру олимпиады по математике 2009-2010 уч. г.

Подготовка учащихся к городскому туру олимпиады по математике2009-2010 уч. г. Материал подготовила методист по математике Шонохова Е.Н.

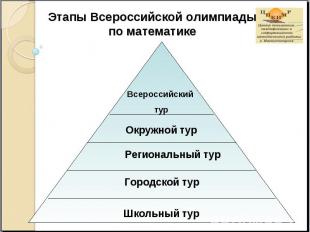
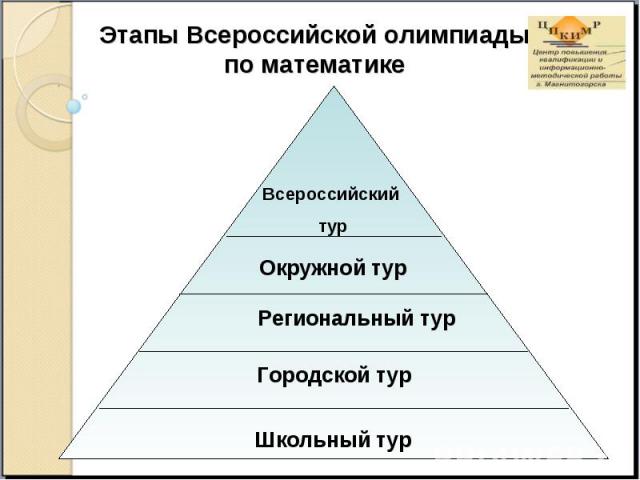
Этапы Всероссийской олимпиады по математике

Внутриклассная олимпиада Формы проведения:домашняяочнаязаочнаядистанционная

Общие принципыформирования комплектов заданий математических олимпиад (внутриклассная олимпиада): нарастание сложности заданий от первого к последнему;трудность должна быть такой, чтобы: с первым заданием могли успешно справиться примерно 70% участников; со вторым – более 50%; с третьим – около 20%; с последними – лучшие из участников олимпиады.

Общие принципы формирования комплектов заданий математических олимпиад (внутриклассная олимпиада): по содержанию: задачи должны быть разнообразными;некоторые из них должны допускать различные решения; для решения задачи необходимо существенно использовать учебный материал; задачи должны обладать эстетическими достоинствами; вызывать желание думать над ними.

Тематическое разнообразие заданий (внутриклассная олимпиада): в комплект должны входить задачи по геометрии, алгебре, комбинаторике; в младших классах – по арифметике, логические задачи; в старших классах желательно включение задач по теории чисел, тригонометрии, стереометрии, математическому анализу. При этом:допустимо и даже рекомендуется включение в варианты задач, объединяющих различные разделы школьной математики;недопустимо включение задач по разделам математики, не изученным по всем базовым учебникам по математике, алгебре и геометрии в соответствующем классе к моменту проведения олимпиады. 

Тематика олимпиадных заданий теория делимости чисел. НОД и НОК;задачи на геометрические преобразования (движение, симметрия, поворот, комбинация преобразований и т.п.);простые и сложные проценты;геометрические задачи на доказательство;уравнения в натуральных или целых числах;применение обратных тригонометрических функций в решении уравнений, неравенств, систем;комбинаторика, элементы теории вероятностей;модуль и параметр;задачи на смекалку, ребусы, головоломки;теория графов;задачи на разливание, разбиение, взвешивание, перебор, выбор;задачи на разрезание, раскрашивание;логические задачи;принцип Дерихле;метод математической индукции;функциональные уравнения;танграмы, пентамино, оригами, домино, игральные кости, игральный кубик, шашки, игральные карты, шахматы;

Время проведения(школьный тур ) Рекомендуемое время проведения олимпиады: для 5-6 классов – 2 урока; для 7-8 классов – 3 урока;для 9-11 классов – 4 урока.

Школьный тур олимпиады по математике Задания для проведения школьного тура 2009 -2010 уч. г., указания, решения, ответы, рекомендации по оцениванию работ даны на диске августовской секции учителей математикиОбратите внимание на уточненные критерии по оцениванию заданий школьного тура и форму протокола заседания школьного жюри

Из ПОЛОЖЕНИЯ о городской олимпиаде школьников по математике: 1. …участниками городского тура могут быть победители школьной олимпиады по одному участнику от параллели (общеобразовательные классы) и до трех – от классов с углубленным изучением предмета. Призеры городской олимпиады прошлого года так же имеют право участия в олимпиаде 2009-2010уч. года сверх квоты представительства ;2…. победителем городской олимпиады в личном первенстве признается участник, выполнивший не менее 60% от суммарного количества баллов за олимпиадные задания.

Городской тур олимпиады по математике (2009 -2010 уч. г.) 8 – 11 кл. Дата проведения: 3 ноября 2009 г. Дата подачи заявки: до 17 октября 2009 г. Место проведения: МЛ № 1Время: 10.006 – 7 кл. Дата проведения: 3 ноября 2009 г. Дата подачи заявки: до 17 октября 2009 г. Место проведения: МОУ «СОШ № 26»Время: 10.00

Заявка школы № ____________ на участие в городской олимпиаде школьников по математике (2009 -2010 уч. г.) Директор ОУ: _________ (подпись с расшифровкой)М.П.

Заявка лицея ____________ на участие в городской олимпиаде школьников по математике (2009 -2010 уч. г.) Директор ОУ: _________ (подпись с расшифровкой)М.П.

Апелляция по результатам городского тура олимпиады по математике: 6 – 11 кл.Дата проведения: 7 ноября 2009г.Время проведения: 14.00Место проведения: МЛ № 1

Из ПОЛОЖЕНИЯ о городской апелляционной комиссии: 1….на процедуре апелляции имеет право присутствовать участник олимпиады, а также учитель в роли наблюдателя, не вмешивающегося в процесс апелляции. В случае невозможности присутствия ребенка на апелляции, его работу апелляционная комиссия рассматривает в присутствии учителя, но без его вмешательства.2…недопустимым является показ работ других участников олимпиады и сравнение результатов.

Рекомендации по подготовке школьников к олимпиаде по математике: 1). Проанализировать информацию по итогам олимпиады по математике 2008 - 2009 учебного года. 2). Практиковать творческие отчеты учителей по работе с одаренными детьми с целью обмена опытом. 3). Продолжать пополнять банк олимпиадных заданий. Создать для каждой параллели папку «В помощь участнику олимпиады» (задания, решения, рекомендации) с целью организации самостоятельной подготовки учащихся под руководством учителя в течение всего учебного года. 4). Вести отслеживание результатов индивидуального участия школьников в олимпиаде и других математических соревнованиях в динамике (начиная с 4 класса). Своевременно использовать эту информацию для формирования портфолио ученика и учителя. 5). Шире использовать возможности вариативного образования; включать в учебный процесс спецкурсы, факультативы, элективные курсы, усиливающие прикладную, практическую направленность обучения математики.

Рекомендации по подготовке школьников к олимпиаде по математике: 6). Провести школьный тур олимпиады по единым текстам, предложенным методистом ГМЦ. Качественно осуществлять отбор школьников на участие в городском туре математической олимпиады. 7). Продолжать учить учащихся процедуре апелляции. 8). Активнее привлекать учащихся к другим видам математических соревнований (международная интеллектуальная конкурс - игра «Кенгуру», дистанционная эвристическая олимпиада, олимпиады ВЗМШ, региональные олимпиады, проводимые на базе южноуральских вузов (МаГУ, МГТУ, ЮрГУ, ЧелГУ), УРФО и т.д. ) 9). Использовать в работе с одаренными детьми наиболее заметные издания «олимпиадной» литературы по математике, Интернет-ресурсы.

Литература: Е.В. Галкин. Нестандартные задачи по математике. Алгебра: учеб. пособие для учащихся 7 – 11 кл. - Челябинск: «Взгляд»,2004Е.В. Галкин. Нестандартные задачи по математике. Задачи с целыми числами:: Учеб. пособие для учащихся 7 – 11 кл. Челябинск: «Взгляд», 2005.Готовимся к экзаменам по алгебре (9 класс.). 1, 2, 3 выпуски / авт.А.К.Дьячков и др.- Челябинск: НП ИЦ « РОСТ», ООО «ЮжУралИнформ», 2004, 2005.Д.В. Клименченко. Задачи для любознательных: Кн. для учащихся 5 – 6 кл. ср. шк.-М.: Просвещение, 1992.А.Р. Рязановский, Е.А. Зайцев. Математика 5 – 11 кл.: Дополнительные главы к уроку математики. – М.: Дрофа, 2001. Ф.Ф. Нагибин, Е.С. Канин. Математическая шкатулка: Пособие для учащихся. – М.: Просвещение, 1984.Н.Б.Васильев, А.А. Егоров. Задачи Всесоюзных математических олимпиад. – М.: Наука, 1988.Шарыгин И.Ф. Решение задач.- М.: Просвещение, 1994.Лоповок Л.М. Тысяча проблемных задач по математике - М.: Просвещение, 1995.Агаханов Н.Х. и др. Математические олимпиады школьников,9.-М.: Просвещение,1997. Журнал «КВАНТ», с1970г.и др