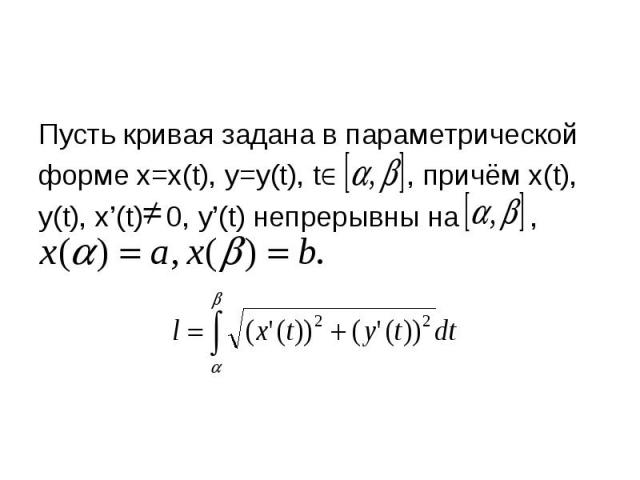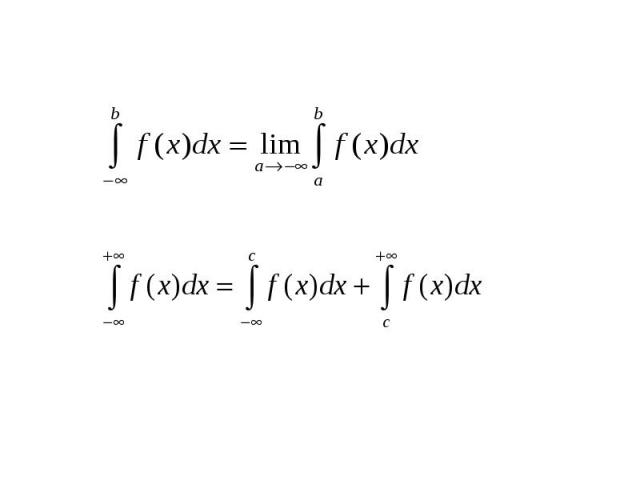Презентация на тему: Определенный и несобственный интегралы

ОПРЕДЕЛЕННЫЙ И НЕСОБСТВЕННЫЙ ИНТЕГРАЛЫ.
![Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называетс Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называетс](https://fs1.ppt4web.ru/images/95284/133989/310/img1.jpg)
Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называется , если этот предел существует и не зависит от способа разбиений [a,b] на и от выбора точек . Определенный интеграл обозначается: Числа a и b называются соответственно нижним и верхним пределами интегрирования.
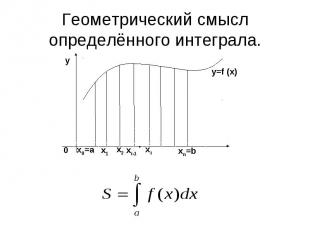
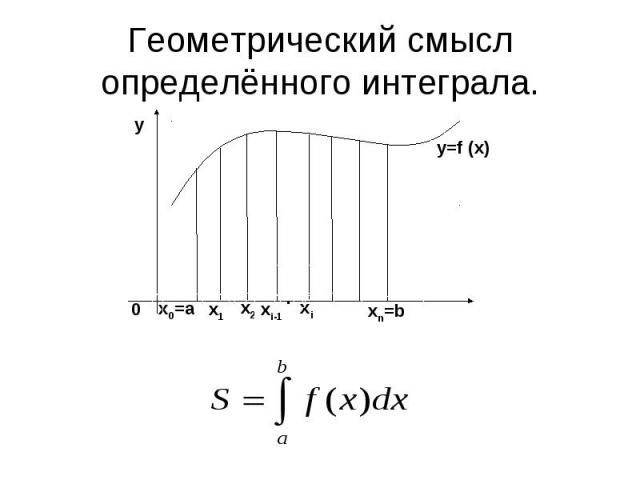
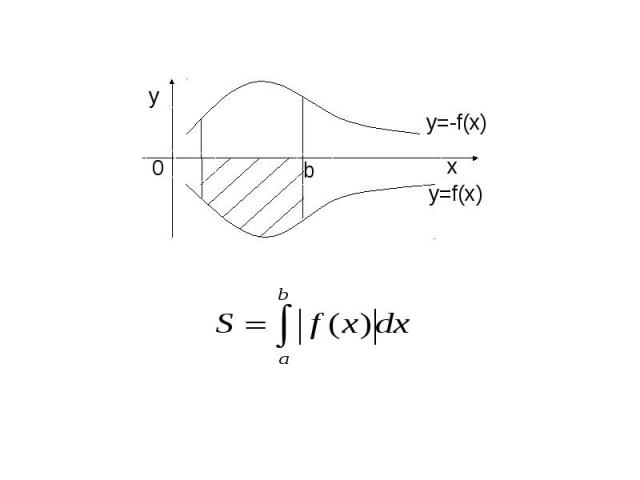
Геометрический смысл определённого интеграла.

Свойства определённого интеграла. 1. 2. 3. , k-любое число 4. 5.Аддитивность определённого интеграла. Для любых чисел a,b,c справедливо:

Формула Ньютона-Лейбница. Если F(x) есть какая-либо первообразная от непрерывной на [ , ] функции f(x), то справедлива формула Ньютона-Лейбница:
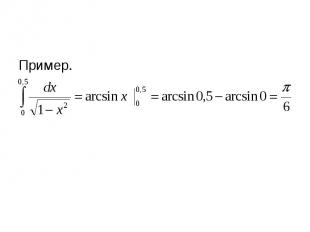
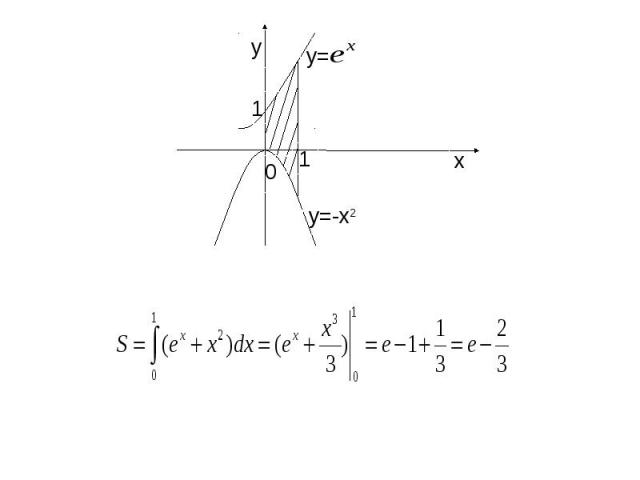
Пример. Пример.
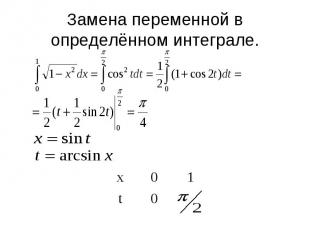
Замена переменной в определённом интеграле.

Интегрирование по частям в определённом интеграле.
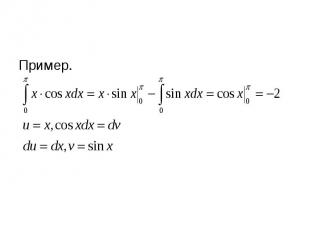
Пример. Пример.

Геометрические приложения определенного интеграла.
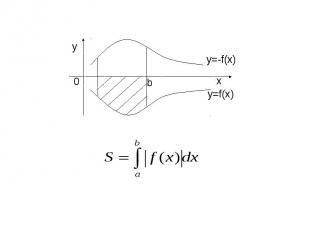
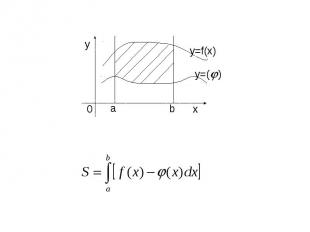
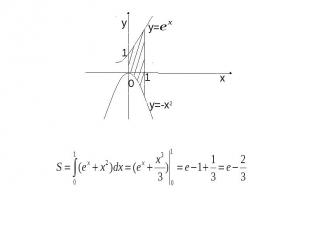

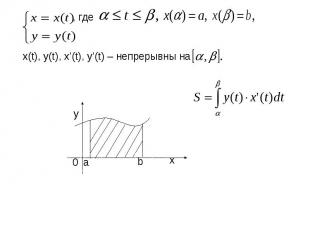


Вычисление длины дуги кривой.
![Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пус Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пус](https://fs1.ppt4web.ru/images/95284/133989/310/img17.jpg)
Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ].
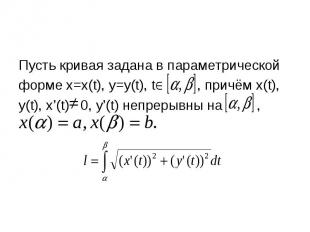
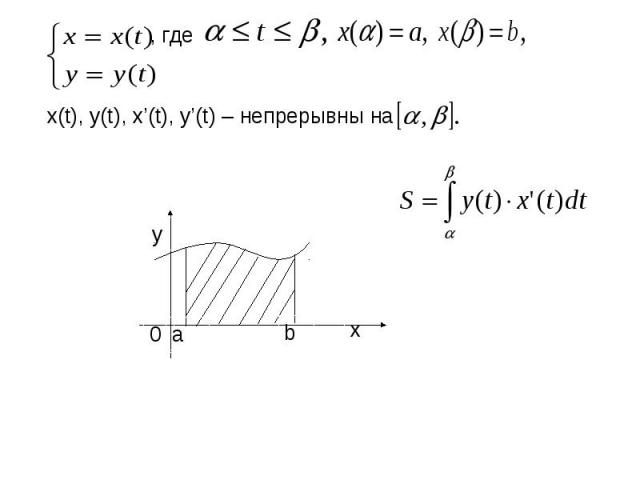
Пусть кривая задана в параметрической Пусть кривая задана в параметрической форме x=x(t), y=y(t), t , причём x(t), y(t), x’(t) 0, y’(t) непрерывны на ,

Несобственный интеграл. Если существует конечный (b> ), то этот предел называется несобственным интегралом функции f(x) на промежутке [ ; ) и обозначают
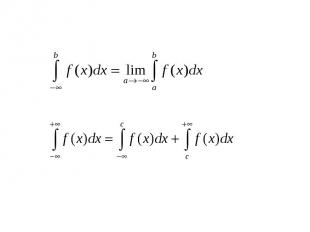

Пример. Пример.

Функции нескольких переменных.

Определение Функцией двух переменных называется правило, по которому каждой упорядоченной паре чисел (x;y), принадлежащей множеству M, ставится в соответствие единственное действительное число z, принадлежащее множеству L. Множество M называется областью определения функции. Множество L называется областью значения функции при условии, что каждое z L соответствует хотя бы одной паре (x;y) M. Функцию двух переменных обозначают: z=f(x; y).

Частные производные.

Частные производные по x. Предел , если он существует, называется частной производной (I порядка) функции z=f(x,y) по x в точке и обозначается: ; ; .

Частные производные по y. называется частной производной (I порядка) функции z=f(x,y) по y в точке и обозначается: ; ; .

Частные производные высших порядков.

Пример. Пример. . Вычислить частные производные II порядка функции. , , , , , .
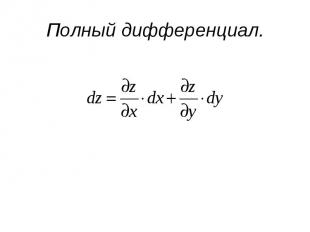
Полный дифференциал.

Скалярное поле. Часть пространства или всё пространство, в каждой точке p(x,y,z) которого задана скалярная функция U=F(x, y, z)=F(p), называется скалярным полем, а функция U= F(p) называется функцией поля. Пример. Найти полный дифференциал функции в произвольной точке. , . Следовательно .

Производная по направлению.

Градиент

Экстремумы функции двух переменных.

Необходимое условие существования экстремума. Пусть функция z=f(x, y) в точке имеет экстремум и пусть существует и . Тогда ,

Достаточное условие существования экстремума. Пусть для функции z=f(x, y) в критической точке существуют производные , , . Выражение назовём дискриминантом функции z=f(x, y) в точке . Возможны три случая: 1) >0 , тогда точка – точка экстремума: при >0 – точка минимума; при <0 – точка максимума. 2) <0, тогда не является точкой экстремума.

Пример исследовать на экстремум функцию Пример исследовать на экстремум функцию Решение. ; . Решая систему получим четыре стационарные точки

Продолжение примера. Проверим достаточное условие экстремума в каждой из точек. ; ; . . Для точки : ; ; ; . Значит, в точке экстремума нет. Для точки : , . В точке функция имеет минимум. Аналогично, проверяют точки и .


![Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называется , если этот предел существует и не зависит от способа разбиений [a,b] на и от выбора точек . Определенный интеграл обозначается: Числа a и b называются соответственно … Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называется , если этот предел существует и не зависит от способа разбиений [a,b] на и от выбора точек . Определенный интеграл обозначается: Числа a и b называются соответственно …](https://fs1.ppt4web.ru/images/95284/133989/640/img1.jpg)

![Формула Ньютона-Лейбница. Если F(x) есть какая-либо первообразная от непрерывной на [ , ] функции f(x), то справедлива формула Ньютона-Лейбница: Формула Ньютона-Лейбница. Если F(x) есть какая-либо первообразная от непрерывной на [ , ] функции f(x), то справедлива формула Ньютона-Лейбница:](https://fs1.ppt4web.ru/images/95284/133989/640/img4.jpg)

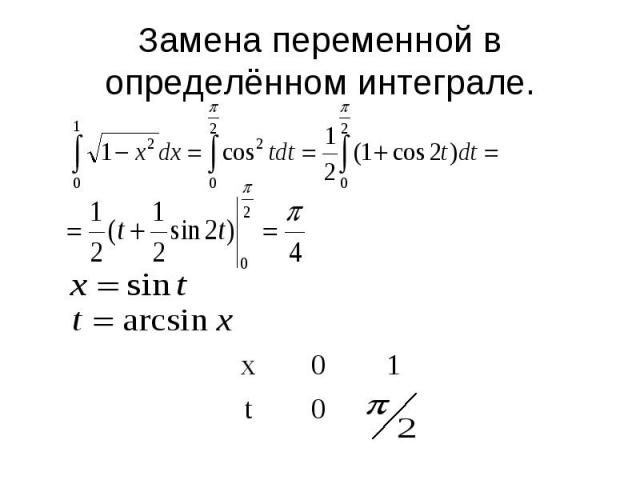

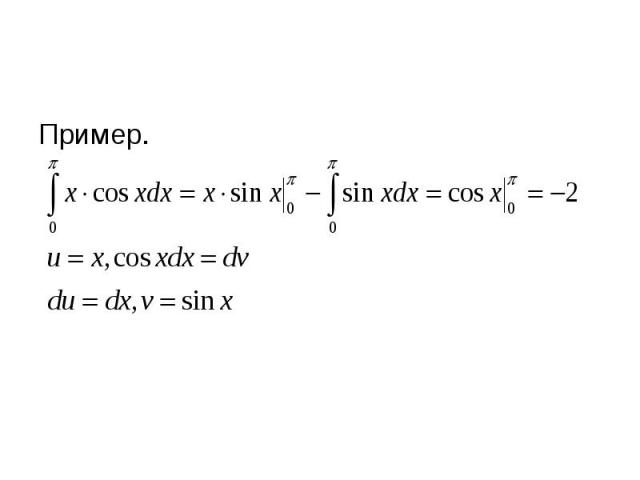

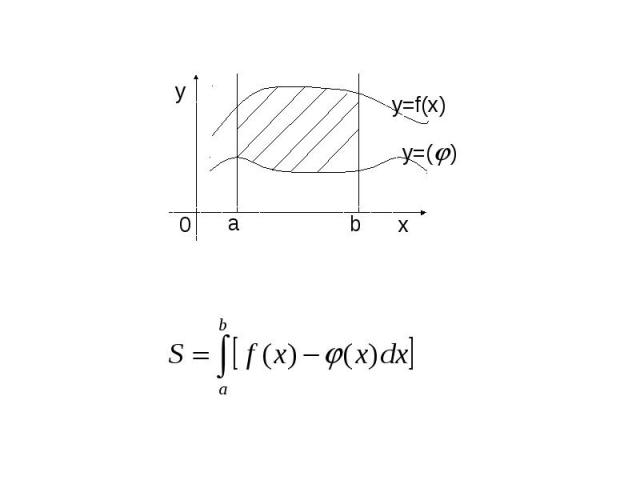



![Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ]. Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ].](https://fs1.ppt4web.ru/images/95284/133989/640/img17.jpg)