Презентация на тему: Задачи линейного программирования

Задачи линейного программирования Лекция 3

Линейное программирование Методы линейного программирования используют в прогнозных расчетах, при планировании и организации производственных процессов. Линейное программирование – это область математики, в которой изучаются методы исследования и отыскания экстремальных значений некоторой линейной функции, на аргументы которой наложены линейные ограничения.

Такая линейная функция называется целевой, а набор количественных соотношений между переменными , выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Слово программирование введено в связи с тем, что неизвестные переменные обычно определяют программу или план работы некоторого субъекта.

Совокупность соотношений, содержащих целевую функцию и ограничения на ее аргументы, называется математической моделью задачи оптимизации. ЗЛП записывается в общем виде так: при ограничениях

Здесь -неизвестные, -заданные постоянные величины. Ограничения могут быть заданы уравнениями. Наиболее часто встречаются задачи в виде: имеется ресурсов при ограничениях. Нужно определить объемы этих ресурсов , при которых целевая функция будет достигать максимума (минимума), т. е. найти оптимальное распределение ограниченных ресурсов. При этом имеются естественные ограничения >0.

При этом экстремум целевой функции ищется на допустимом множестве решений, определяемом системой ограничений, причем все или некоторые неравенства в системе ограничений могут быть записаны в виде уравнений.

В краткой записи ЗЛП имеет вид: при ограничениях

Для составления математической модели ЗЛП необходимо : 1)обозначить переменные; 2)составить целевую функцию; 3)записать систему ограничений в соответствии с целью задачи; 4)записать систему ограничений с учетом имеющихся в условии задачи показателей. Если все ограничения задачи заданы уравнениями, то модель такого вида называется канонической. Если хоть одно из ограничений дано неравенством, то модель неканоническая.

Примеры задач, которые сводятся к ЗПЛ. задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача об ассортименте); задача на максимум выпуска продукции при заданном ассортименте; задача о смесях (рационе, диете и т.д.); транспортная задача; задача о рациональном использовании имеющихся мощностей; задача о назначениях.

1.Задача оптимального распределения ресурсов. Предположим, что предприятие выпускает различных изделий. Для их производства требуется различных видов ресурсов (сырья, рабочего и машинного времени, вспомогательных материалов). Эти ресурсы ограничены и составляют в планируемый период условных единиц. Известны также технологические коэффициенты , которые указывают, сколько единиц i-го ресурса требуется для производства изделия j-го вида. Пусть прибыль, получаемая предприятием при реализации единицы изделия j-го вида , равна . В планируемый период все показатели предполагаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей. Экономико-математическая модель задачи

Целевая функция представляет собой суммарную прибыль от реализации выпускаемой продукции всех видов. В данной модели задачи оптимизация возможна за счет выбора наиболее выгодных видов продукции. Ограничения означают , что для любого из ресурсов его суммарный расход на производство всех видов продукции не превосходит его запасы.

Примеры

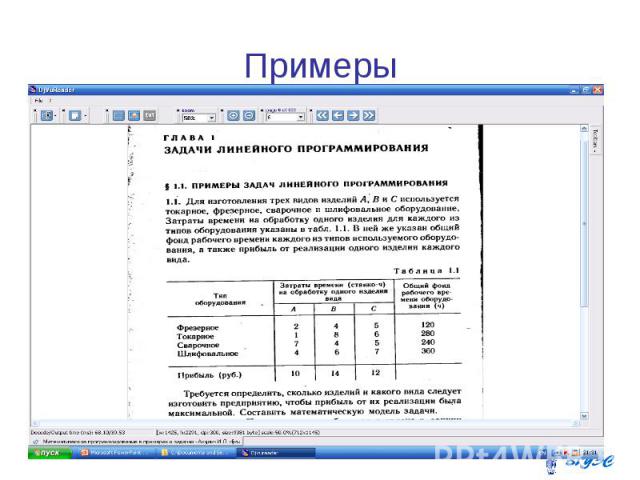
Допустим, что будет изготовлено изделий вида А, -изделий вида В и -изделий вида С. Тогда для производства такого количества изделий потребуется затратить станко-часов фрезерного оборудования. Так как общий фонд рабочего времени станков данного типа не может превышать 120, то должно выполняться неравенство

Рассуждая аналогично, можно составить систему ограничений

Теперь составим целевую функцию. Прибыль от реализации изделий вида А составит 10 , от реализации -изделий вида В -14 и от реализации -изделий вида С-12 Общая прибыль от реализации всех изделий составит

Таким образом, приходим к следующей ЗЛП: Требуется среди всех неотрицательных решений системы неравенств найти такое, при котором целевая функция принимает максимальное значение.

Пример 2 Продукцией гормолокозавода являются молоко, кефир и сметана, расфасованные в тару. На производство 1 т молока, кефира и сметаны требуется соответственно1010,1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машино-часов. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 часов.

Всего для производства цельномолочной продукции завод может использовать 136000 кг молока. Основное оборудование может быть занято в течение 21,4 машино-часов, а автоматы по расфасовке сметаны – в течение 16,25 часов. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100 т молока, расфасованного в бутылки. На производство другой продукции нет ограничений.

Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной. Составить математическую модель задачи.

Решение Пусть завод будет производить т молока, т кефира и т сметаны. Тогда ему необходимо кг молока. Так как завод может использовать ежедневно не более 136000 кг молока, то должно выполняться неравенство

Ограничения на время по расфасовке молока и кефира и по расфасовке сметаны . Так как ежедневно должно вырабатываться не менее100 т молока, то . По экономическому смыслу

Общая прибыль от реализации всей продукции равна руб. Таким образом, приходим к следующей задаче: при ограничениях Так как целевая функция линейная и ограничения заданы системой неравенств, то эта задача является ЗЛП.

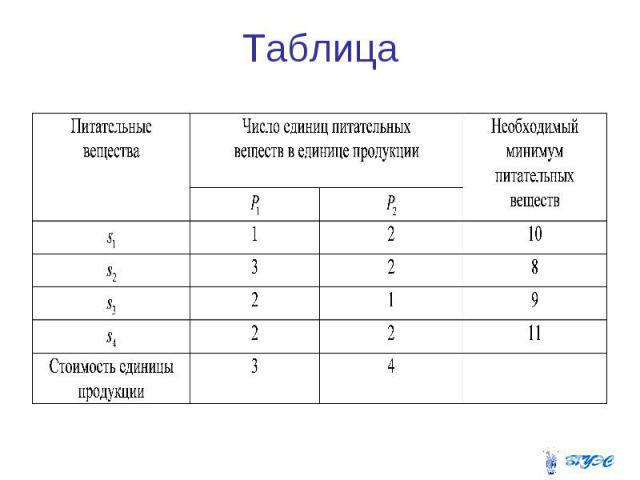
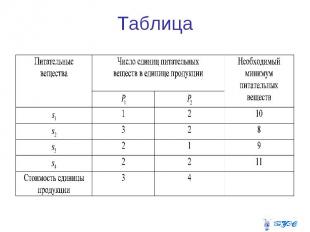
Задача о смесях. Имеется два вида продукции , содержащие питательные вещества (жиры, белки и т.д.)

Таблица

Решение Общая стоимость рациона при ограничениях с учетом необходимого минимума питательных веществ

Математическая постановка задачи: составить дневной рацион , удовлетворяющий системе ограничений и минимизирующий целевую функцию. В общем виде к группе задач о смесях относятся задачи по отысканию наиболее дешевого набора из определенных исходных материалов, обеспечивающих получение смеси с заданными свойствами. Полученные смеси должны иметь в своем составе n различных компонентов в определенных количествах, а сами компоненты являются составными частями m исходных материалов.

Введем обозначения: -количество j-го материала, входящего в смесь; -цена материала j-го вида; -это минимально необходимое содержание i-го компонента в смеси. Коэффициенты показывают удельный вес i-го компонента в единице j-го материала

Экономико-математическая модель задачи. Целевая функция представляет собой суммарную стоимость смеси, а функциональные ограничения являются ограничениями по содержанию компонентов в смеси: смесь должна содержать компоненты в объемах, не менее указанных.

Задача о раскрое На швейной фабрике ткань может быть раскроена несколькими способами для изготовления нужных деталей швейных изделий. Пусть при j-ом варианте раскроя изготавливается деталей i-го вида, а величина отходов при данном варианте раскроя равна Зная, что деталей i-го вида следует изготовлять штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.

Решение. Предположим, что по j-ому варианту раскраивается сотен ткани. Поскольку при раскрое ткани по j-ому варианту получается деталей i-го вида , по всем вариантам раскроя из используемых тканей будет получено Общая величина отходов по всем вариантам раскроя составит

Таким образом, приходим к следующей задаче: Найти минимум функции при условии, что ее переменные удовлетворяют ограничениям

Общая задача линейного программирования. Опр.1.Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (1) при условиях (2) где -заданные постоянные величины и

Опр.2.Функция (1) называется целевой, а условия (2)-ограничениями задачи. Опр.3. Совокупность чисел , удовлетворяющих ограничениям задачи (1)-(2), называются допустимым решением (или планом).

Основная задача ЛП Опр.4. Основной , или канонической ЗЛП называется задача, состоящая в определении значения целевой функции при условии, что система ограничений представлена в виде системы уравнений:

Если требуется для удобства или по смыслу задачи перейти от одной формы записи к другой , то поступают следующим образом. Если требуется найти минимум функции, то можно перейти к нахождению максимума, умножив целевую функции на (-1). Ограничение –неравенство вида можно преобразовать в равенство добавлением к его левой части неотрицательной дополнительной переменной , а ограничение неравенство вида - в ограничение- равенство вычитанием из его левой части дополнительной неотрицательной переменной.

Пример. Записать в форме основной задачи ЛП задачу: найти максимум функции при условиях

Перейдем от ограничений –неравенств к ограничениям-равенствам. У нас имеется 4 неравенства, поэтому введем 4 дополнительные переменные. Тогда запишем уже основную задачу линейного программирования: максимизировать функцию при условиях

Свойства основной ЗЛП. Перепишем ЗЛП в векторной форме: найти максимум функции при условиях Здесь

План называется опорным, если все компоненты базисного решения системы ограничений канонической задачи линейного программирования неотрицательны. Число положительных компонент опорного плана не может быть больше m, т.е.числа уравнений в ограничениях.

Опорный план называется невырожденным, если он содержит m положительных компонент. В противном случае он называется вырожденным. План, при котором целевая функция ЗЛП принимает свое максимальное (минимальное ) значение , называется оптимальным.