Презентация на тему: Численные методы решения СЛАУ

Методы решения СЛАУ Метод Гаусса Аx=f,

Теорема Крамера Если определитель матрицы не равен нулю , то решение СЛАУ существует и единственно. Метод Гаусса, первый шаг

Метод Гаусса, шаг-s

Решение СЛАУ методом Гаусса

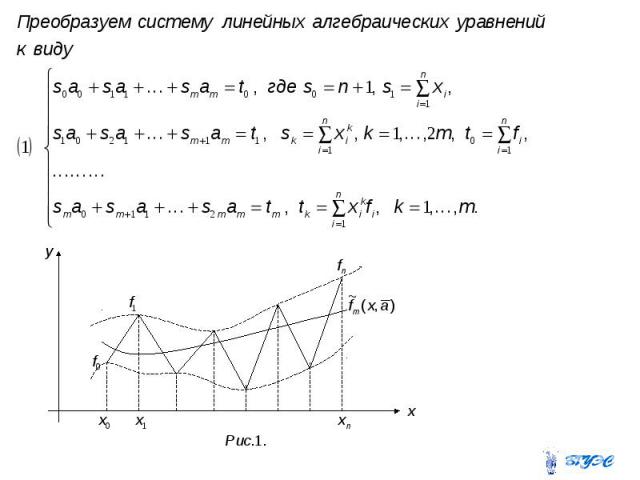
Преобразуем расширенную матрицу Преобразуем расширенную матрицу

Метод LU- разложения

Прямой и обратный ходы Решить систему (прямой ход) Чтобы найти х, надо решить систему (обратный ход) Пример: решить СЛАУ:

Найдем матрицы Найдем матрицы

Прямой ход Решим систему

Обратный ход Решим систему

Метод прогонки Матрица А - трёхдиагональная

Обратный ход метода прогонки Обратный ход метода прогонки

Достаточное условие корректности и устойчивости метода прогонки: Достаточное условие корректности и устойчивости метода прогонки:

Прямой ход. Прямой ход.

Итерационные методы Метод простых итераций (МПИ)

Теорема 1 (о достаточном условии сходимости МПИ: Теорема 1 (о достаточном условии сходимости МПИ: Условия сходимости выполняются, если

Пример.

Количество итераций вычисляется по (1) и K=5 Количество итераций вычисляется по (1) и K=5

Задание к первой лабораторной работе

Отделение корней Теорема.

Метод половинного деления

Оценка числа итераций Оценка числа итераций Пример.

Метод хорд К условиям 1), 2), 3), 4) МДП добавляется условие

Пример. Пример.

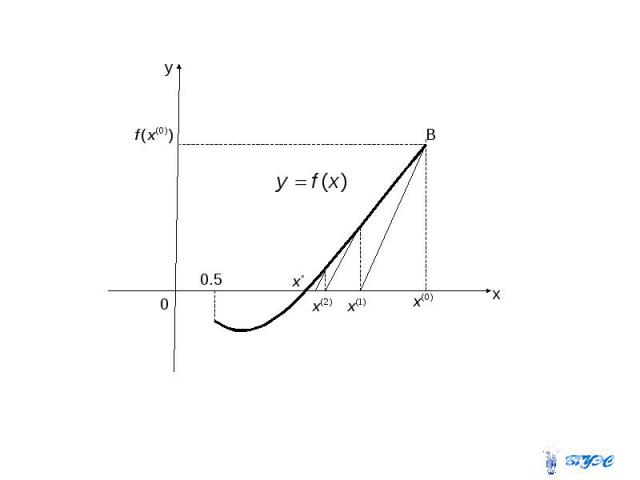
Метод Ньютона Теорема (достаточные условия сходимости метода Ньютона).

Пример. Пример.

Метод простых итераций

Задание ко второй лабораторной работе

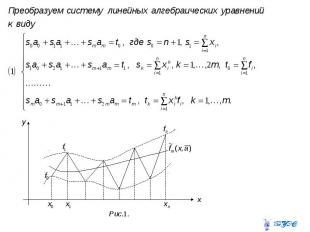
Cглаживание на основе сплайнов Интерполяционные кубические сплайны

Задание к третьей лабораторной работе

Квадратурные формулы Ньютона-Котеса

Формула трапеций

Формула Симпсона

Вычисление определенного интеграла с заданной точностью

Пример.

Задание к четвертой лабораторной работе

Квадратурная формула Чебышева