Презентация на тему: Дифференциальные уравнения высших порядков

Глава 2. Дифференциальные уравнения высших порядков.

1. Общие сведения.

Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным уравнением порядка высшее первого. Уравнение порядка “ ”- или

Теорема: Дано дифференциальное уравнение и система начальных условий , ,…., Если функция непрерывна в окрестностях начального условия и имеет непрерывные частные производные по , то существует и притом единственное решение уравнения, определенное и непрерывное в некотором интервале содержащем , и удовлетворяющее заданной системе начальных условий.

2.Типы уравнений, допускающих понижение порядка.
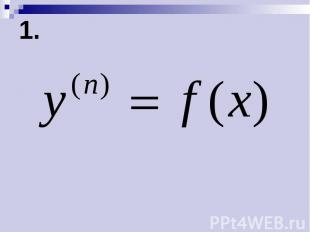
1.

2. Дифференциальное уравнение не содержащее явно и младших производных до (k-1) порядка включительно, допускает понижение порядка на k единиц

3. Уравнение вида также допускает понижение порядка путем замены обоих переменных.

4. Если левая часть уравнения есть точная правая, то порядок уравнения поднимается на единицу путем непосредственного интегрирования. (Это уравнение встречается редко, но к этому виду приводятся некоторые уравнения.)

Линейное дифференциальное уравнение высшего порядка.

Линейным дифференциальным уравнением n-го порядка называется уравнение вида:

Теорема Пусть коэффициент , . Линейное дифференциальное уравнение непрерывно на некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и любой системе начальных условий, если только значение принадлежит интервалу (a;b).

Определение: Уравнение вида называется линейным однородным дифференциальным уравнением.

Определение. Обозначим линейную часть уравнения через , . . Выражение называется линейным дифференциальным оператором от функции .

Свойства линейного дифференциального оператора. 1.Постоянный множитель можно выносить за знак оператора, то есть для любого n размерной дифференциальной функции - свойство однородности. 2.Оператор от суммы двух функций и равен сумме операторов от каждого из слагаемых в отдельности, то есть для любых n раз дифференцируемых функций и верно равенство: - свойство аддитивности

Определение: Линейное дифференциальное однородное уравнение можно записать в виде

Теоремы о свойствах частичных решений Теоремы о свойствах частичных решений

Теорема1. Если функция является решением уравнения , то и функция есть решение этого уравнения.

Теорема2. Если функции и являются решениями уравнения , то и функция есть решение этого уравнения.

Теорема3. Если - частные решения линейного однородного дифференциального уравнения, то их линейная комбинация есть также решение этого уравнения.

Линейная зависимость и независимость функций. Определитель Вронского и его применение.
![Определение. Система функций определенных и непрерывных на отрезке [a;b] называе Определение. Система функций определенных и непрерывных на отрезке [a;b] называе](https://fs1.ppt4web.ru/images/95284/133974/310/img21.jpg)
Определение. Система функций определенных и непрерывных на отрезке [a;b] называется линейно зависимой на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) .

Теорема. Если уравнение линейно зависимо, то хотя бы одну из них можно выразить через остальные.

Если функции системы дифференцируемы n-1 то из них можно построить определитель n-го порядка, который имеет вид Если функции системы дифференцируемы n-1 то из них можно построить определитель n-го порядка, который имеет вид Этот определитель является функцией от х и обозначается Этот определитель называется определителем Вронского

Теорема1. Если функции линейно зависимы, то определитель Вронского тождественно равен 0.

Теорема 2. Если - линейно независимые функции, удовлетворяющие некоторому однородному дифференциальному уравнению n-го порядка, то определитель системы не обращается в ноль ни в одной точке.

Определение. Систему частных решений линейного однородного дифференциального уравнения n-го порядка называют фундаментальной, если она состоит из n независимых функций.

Теорема. Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством фундаментальных систем.

Теорема Если функции образуют фундаментальную систему решений уравнения ,то их линейная комбинация - является общим решением этого уравнения.

Линейное однородное уравнение с постоянным коэффициентом.

Определение. Уравнение вида , г де =const, называется линейным однородным дифференциальным уравнением с постоянным коэффициентом.

Определение. называется характеристическим членом линейного однородного дифференциального уравнения.

Определение. Уравнение называется характеристическим уравнением линейного однородного дифференциального уравнения.

Все корни уравнения Все корни уравнения действительны и различны

линейная комбинация является общим решением линейного однородного дифференциального уравнения.

Все корни различны, но среди них есть комплексные Все корни различны, но среди них есть комплексные

формулы Эйлера :

паре комплексных сопряженных корней паре комплексных сопряженных корней можно поставить в соответствие частных решений

Доказать самостоятельно линейную независимость системы частных решений Доказать самостоятельно линейную независимость системы частных решений

При доказательстве нигде не учитывается, что - действительное число поэтому когда пара корней является двойной, то ей соответствует четыре частных решения следующих видов: При доказательстве нигде не учитывается, что - действительное число поэтому когда пара корней является двойной, то ей соответствует четыре частных решения следующих видов:

Вывод: Задача нахождения общего решения линейного однородного дифференциального уравнения n – го порядка с постоянным коэффициентом сводится к нахождению всех корней алгебраического уравнения n-ой степени.

3.Линейные неоднородные дифференциальные уравнения.

Определение Линейным неоднородным дифференциальным уравнением называется уравнение вида

Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения): Общее решение линейного неоднородного дифференциального уравнения представляет сумму частного решения этого уравнения и общего решения соответствующего однородного (при g=0), .

Теорема2: Если правая часть неоднородного уравнения есть сумма двух функций, т.е. , то частное решение такого уравнения можно получить как сумму частных решений аналогичных уравнений с правыми частями соответственно и






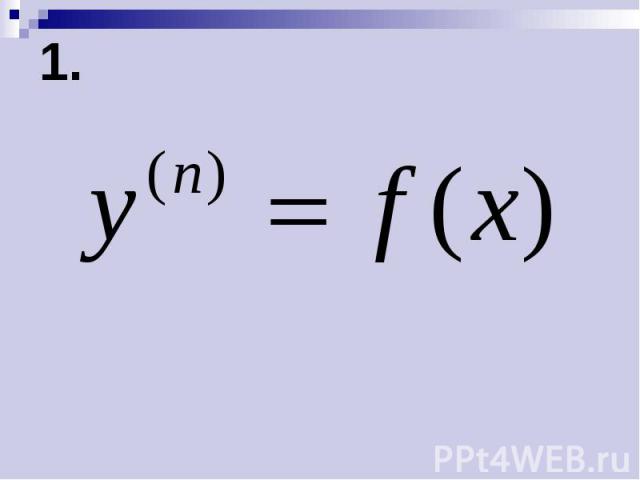





![Теорема Пусть коэффициент , . Линейное дифференциальное уравнение непрерывно на некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и лю… Теорема Пусть коэффициент , . Линейное дифференциальное уравнение непрерывно на некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и лю…](https://fs1.ppt4web.ru/images/95284/133974/640/img11.jpg)









![Определение. Система функций определенных и непрерывных на отрезке [a;b] называется линейно зависимой на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) . Определение. Система функций определенных и непрерывных на отрезке [a;b] называется линейно зависимой на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) .](https://fs1.ppt4web.ru/images/95284/133974/640/img21.jpg)


































