Презентация на тему: 5.Уравнение в полных дифференциалах. Интегрирующий множитель

5.Уравнение в полных дифференциалах. Интегрирующий множитель.

Теорема: Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные и ,представляла собой полный дифференциал некоторой функции , необходимо и достаточно, чтобы во всех точках области было выполнено условие .

Интегрирующий множитель.

Если , то уравнение не является уравнением в полных дифференциалах. Однако это уравнение можно превратить в уравнения в полных дифференциалах умножением на подходящую функцию . Такая функция называется интегрирующим множителем для данного дифференциального уравнения. Если , то уравнение не является уравнением в полных дифференциалах. Однако это уравнение можно превратить в уравнения в полных дифференциалах умножением на подходящую функцию . Такая функция называется интегрирующим множителем для данного дифференциального уравнения.

Практически поступают так: берут выражение , делят на , если не зависит частное от , то находят по формуле , если в противном случае делят на и если частное не зависит от x , то существует и его находят по формуле Практически поступают так: берут выражение , делят на , если не зависит частное от , то находят по формуле , если в противном случае делят на и если частное не зависит от x , то существует и его находят по формуле

6.Дополнительные сведения.

Дифференциальное уравнение может быть также истолковано следующим образом. Пусть - общее решение дифференциального уравнения, т.е. семейство интегрирующих кривых в некоторой области , плоскости , в которой определена функция . Дифференциальное уравнение устанавливает связь между координатами любой точки области и значением производной в этой точке. Зная и точки , можно найти значение производной, т.е. угловой коэффициент касательной к интегрирующей кривой, проходящую через точку .

Рисунок 5 Рисунок 5

Геометрически задача интегрирования дифференциального уравнения заключается в нахождении кривых, которые в каждой своей точке касаются направления, задаваемым полем . Геометрически задача интегрирования дифференциального уравнения заключается в нахождении кривых, которые в каждой своей точке касаются направления, задаваемым полем .

Теорема (Коши). Если функция определена и непрерывна в области плоскости и имеет непрерывную частную производную во всех точках этой области, то, какова бы ни была точка области , всегда существует и притом единственная, функция , которая определена и непрерывна в некотором интервале, содержащим точку , является решением уравнения и принимает при значение .

7. Уравнение первого порядка, не разрешенные относительно производной.

Рассмотрим дифференциальное уравнение , не разрешенное относительно . Рассмотрим дифференциальное уравнение , не разрешенное относительно .

Случай 1. Уравнение первого порядка n-й степени , где n-целое положительное число, , - функции от х и у.

Общие интегралы имеют вид:

Случай 2. Уравнение разрешенное относительно у и не содержащее х . Это уравнение решается методом введения параметра р. Пусть , тогда .

Пусть , тогда . Пусть , тогда .

Случай 3. Уравнение разрешенное относительно х и не содержащее у: . Аналогично: ,

Случай 4. . Уравнения не содержащие х и у, но не обязательно разрешенные относительно у и х. (*) (**)

Случай 5. Уравнение Лагранжа. Уравнение, линейно относительно x и y , т.е. имеющее вид

1-й случай . Его общий интеграл имеет вид , вместе с уравнением он дает общий интеграл уравнения Лагранжа.

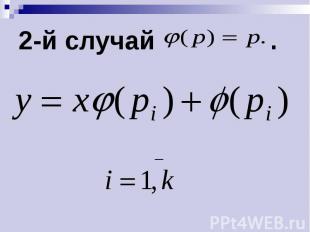
2-й случай .

Случай 6. Уравнение Клеро