Презентация на тему: Уравнение касательной к графику функции в точке

Государственное Образовательное Учреждение Лицей №1523ЮАО г.МоскваЛекции по алгебре и началам анализа10 класс

Лекция № 21Уравнение касательной к графику функции в точке

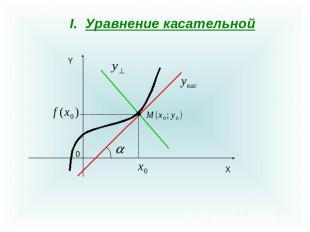
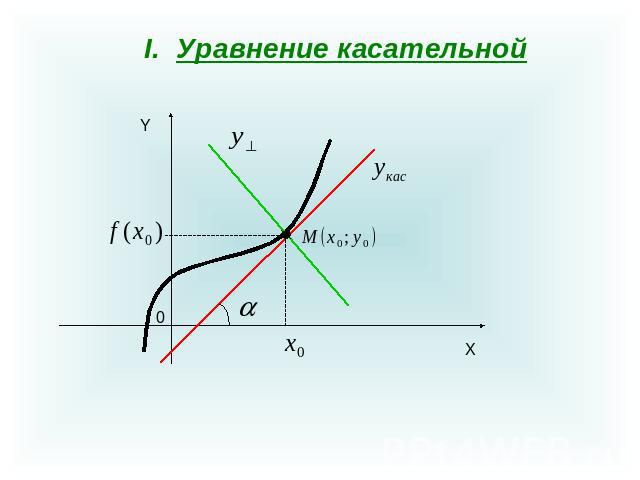
Уравнение касательной

Пусть функция дифференцируема в точке . Прямая, определяемая уравнениемназывается касательной к графику функции в точке .

II. Уравнение нормали.Прямая, перпендикулярная касательной в точке касания , называется нормалью к графику функции в этой точке.

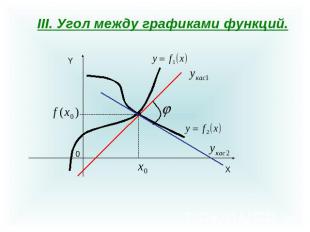
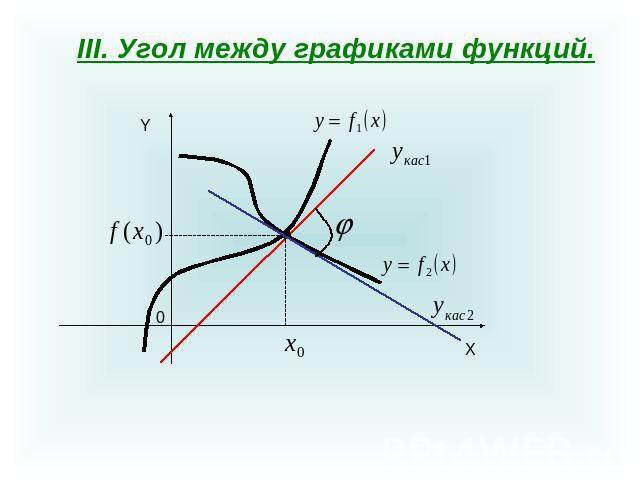
III. Угол между графиками функций.

Под углом между графиками функций и в их общей точке понимают угол между касательными к этим графикам в точке .Если ,то и кривые пересекаются под прямым углом.

IV. Условия параллельности и перпендикулярности двух прямых Пусть прямые заданы уравнениями и . Для того, чтобы эти прямые были параллельны, необходимо и достаточно, чтобы . Для того чтобы эти прямые были перпендикулярны, необходимо и достаточно, чтобы .