Презентация на тему: Уравнение касательной к графику функции

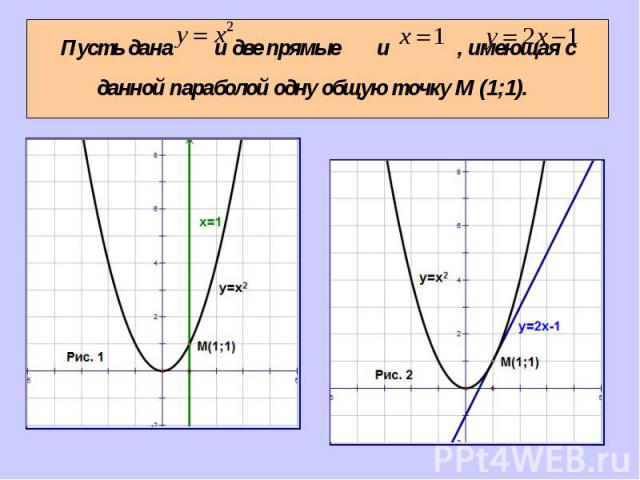
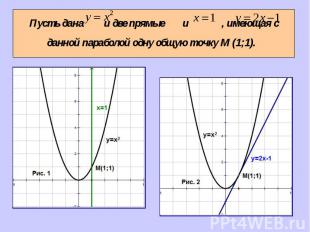
Касательная – это прямая, имеющая с данной кривой одну общую точку.

выясним, что же такое касательная к графику функции в точке, как составить уравнение касательной; выясним, что же такое касательная к графику функции в точке, как составить уравнение касательной; рассмотрим основные задачи на составление уравнения касательной.

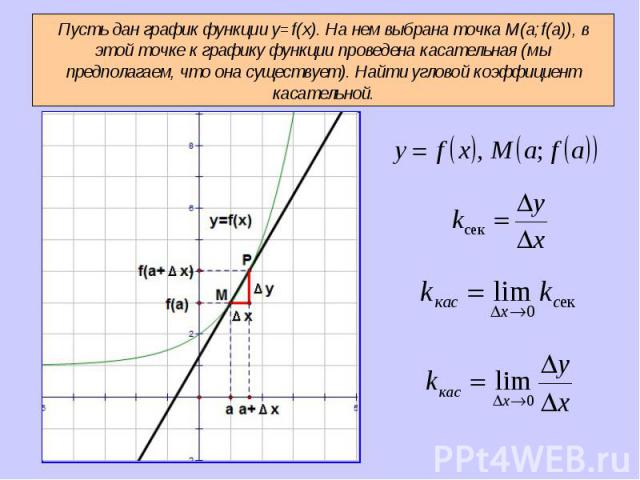
Пусть функция определена в некотором интервале, содержащем внутри себя точку . Дадим аргументу приращение такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции и составим Пусть функция определена в некотором интервале, содержащем внутри себя точку . Дадим аргументу приращение такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции и составим отношение .Если существует предел отношения при , то указанный предел называют производной функции в точке и обозначают .

Производная суммы равна сумме производных. Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения двух функций равна сумме двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции. Производная частного

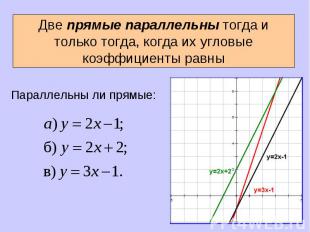
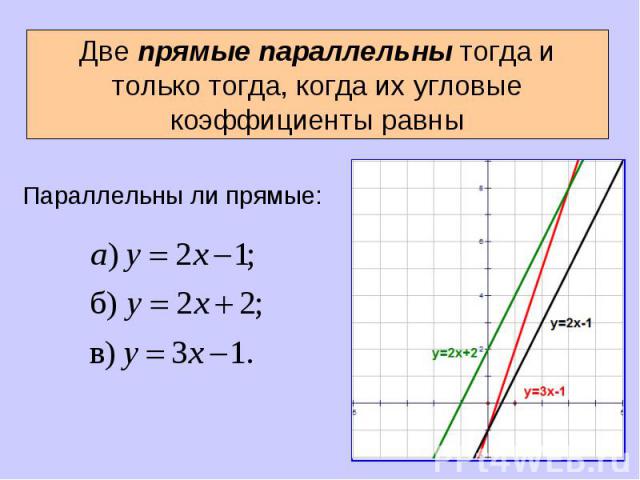
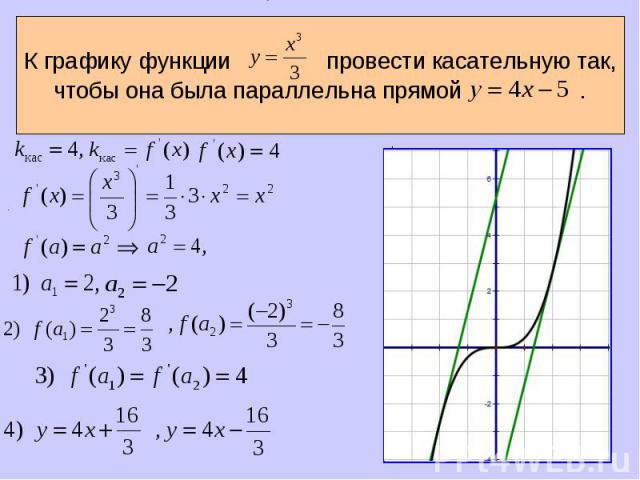
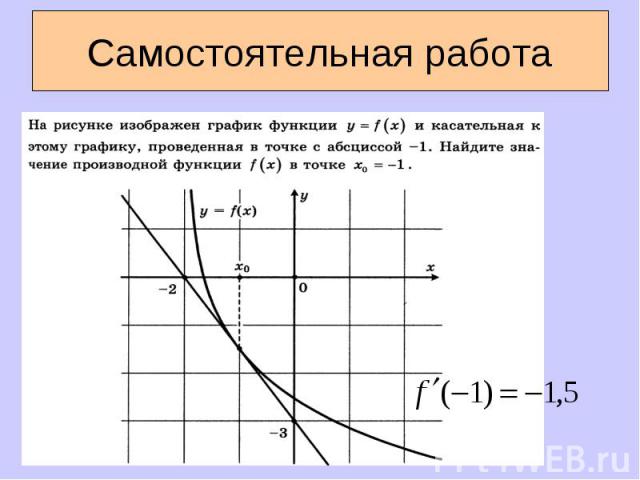
Параллельны ли прямые: Параллельны ли прямые:

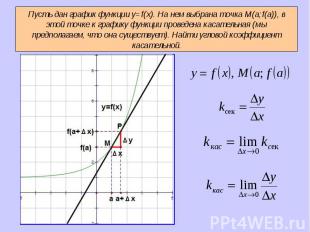
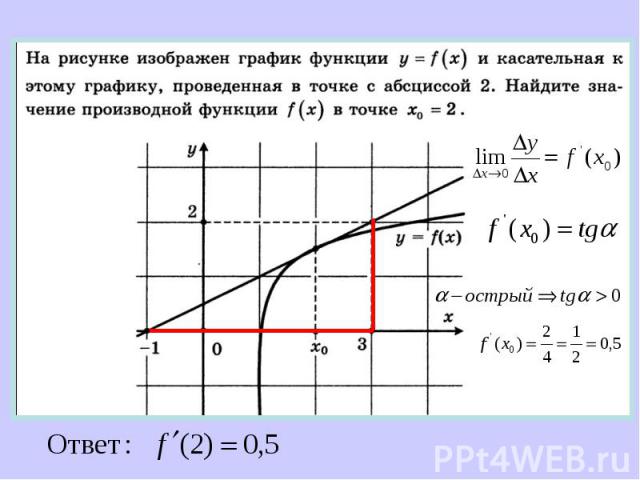
Если к графику функции y = f (x) в точке Если к графику функции y = f (x) в точке можно провести касательную, непараллельную оси у, то выражает угловой коэффициент касательной

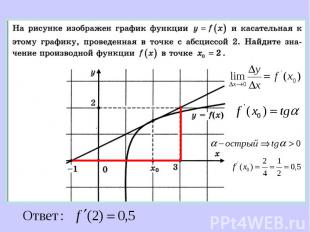
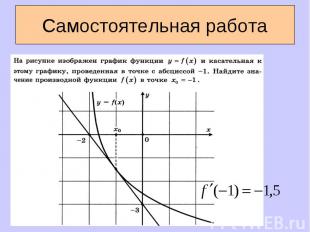
Производная в точке Производная в точке равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. Т.е.

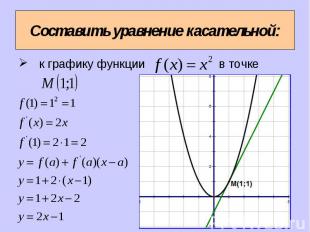
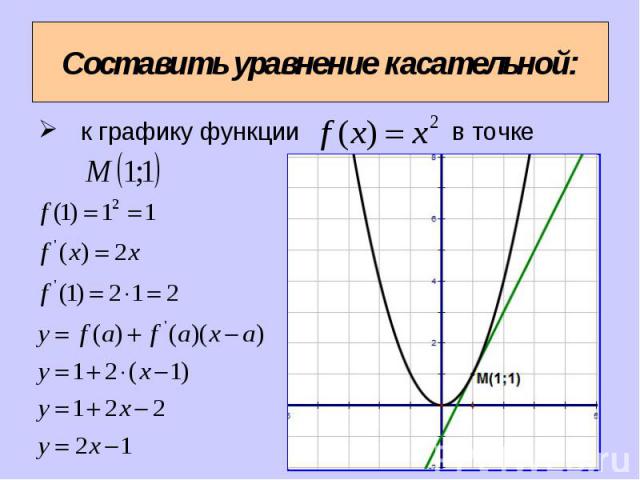
к графику функции в точке к графику функции в точке

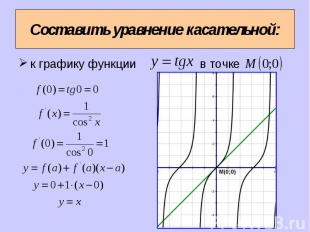
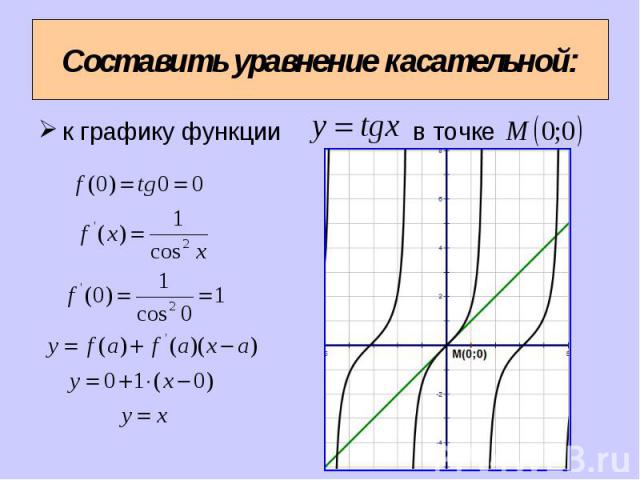
к графику функции в точке к графику функции в точке

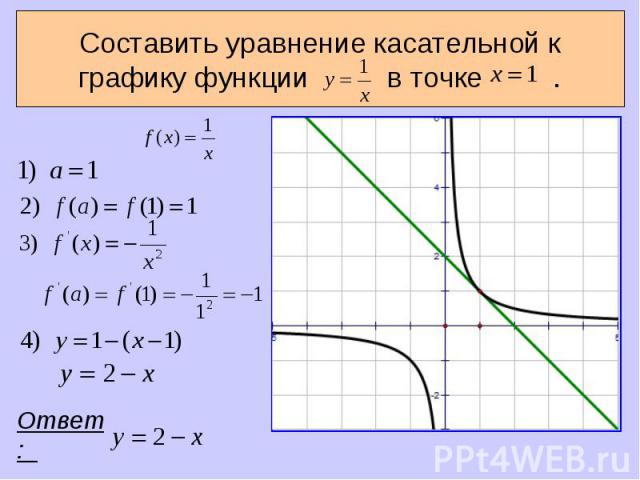
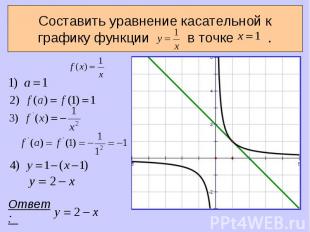
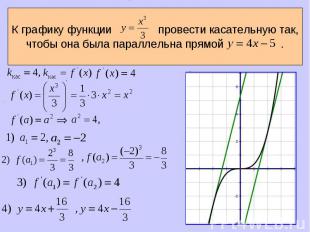
Обозначим абсциссу точки касания буквой x=a. Обозначим абсциссу точки касания буквой x=a. Вычислим . Найдем и . Подставим найденные числа a , в формулу

№ 29.3 (а,в) № 29.3 (а,в) № 29.12 (б,г) № 29.18 № 29.23 (а)

Что называется касательной к графику функции в точке? Что называется касательной к графику функции в точке? В чем заключается геометрический смысл производной? Сформулируйте алгоритм нахождения уравнения касательной?

№ 29.3 (б,г) № 29.3 (б,г) № 29.12 (а,в) № 29.19 № 29.23 (б)

Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009. Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009. Алгебра и начала математического анализа: Задачник, Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009. Алгебра и начала анализа. Самостоятельные и контрольные работы для 10-11 классов. / Ершова А.П., Голобородько В.В. – М.: ИЛЕКСА, 2010 ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под редакцией А.Л.Семенова и И.В.Ященко – M.: Издательство МЦНМО, 2010