Презентация на тему: Основы теории графов

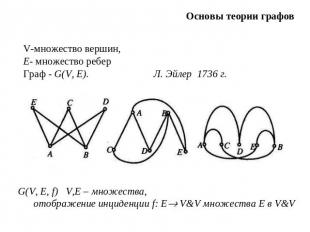
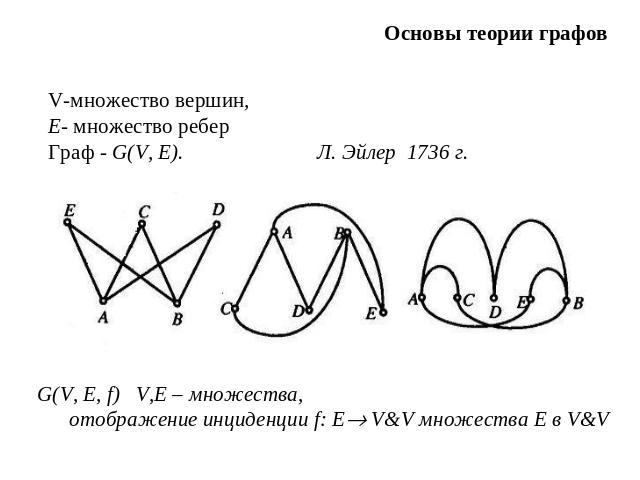
Основы теории графов V-множество вершин,E- множество реберГраф - G(V, Е). Л. Эйлер 1736 г.G(V, Е, f) V,E – множества, отображение инциденции f: Е V&V множества Е в V&V

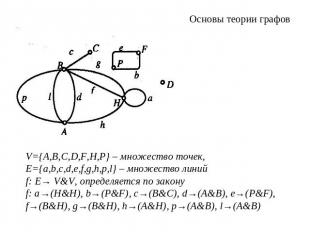
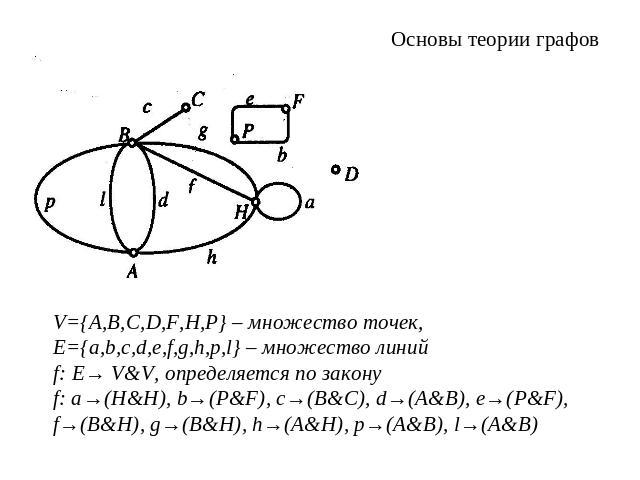
Основы теории графовV={A,В,С,D,F,Н,P} – множество точек, E={a,b,с,d,e,f,g,h,p,l} – множество линийf: Е→ V&V, определяется по закону f: a→(H&H), b→(P&F), c→(B&C), d→(A&B), e→(P&F),f→(B&H), g→(B&H), h→(A&H), p→(A&B), l→(A&B)

Основы теории графовОпределение инцидентности. Пусть задан абстрактный граф G(V, Е, f). Если отображение f сопоставляет ребру е пару вершин (х1&х2), т.е. f(e) = (х1&х2), то ребро е инцидентно вершинам х1 и х2. «ребро е соединяет вершины x1 и x2» «вершины x1 и x2 являются граничными точками ребра е».Если f(е) = (x&x), то ребро называется петлей в вершине х. Определение смежности. Две вершины x1 и x2 графа G(V, Е, f) называются смежными, если в графе существует ребро е, инцидентное этим вершинам.Два ребра графа называются смежными, если существует вершина, инцидентная обоим этим ребрам.

Основы теории графовСтепенью вершины графа называется количество инцидентных ей ребер (для петли степень подсчитывается дважды). Вершины графа называются четными или нечетными в зависимости от четности их степеней. Теорема 1. В любом конечном графе G(V, Е) количество нечетных вершин — четно. Сумма степеней всех вершин равна удвоенному числу ребер графа: ∑ Q(x)=2|E|

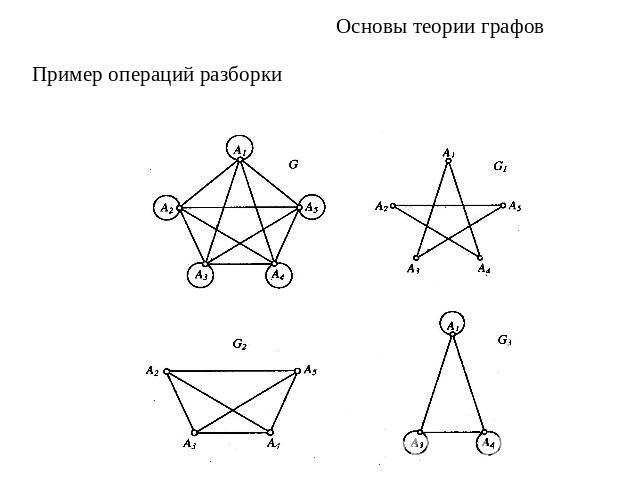
Основы теории графовОперации разборки графа: удаление ребра между двумя вершинами графа. 2) удаление вершины графа вместе со всеми инцидентными ребрами. Подграфом графа G называется такая его часть G1, которая получается из графа G при помощи конечного числаопераций разборки вида 2.Суграфом графа G называется такая его часть G1, которая получается из графа G при помощи конечного числа операций разборки вида 1.

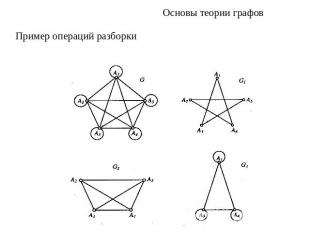
Основы теории графовПример операций разборки

Основы теории графовG(V, Е, f) V={А1,А2,…,Аn} E={a1,a2,…,an}. Конечная последовательность ребер графа a1,a2,…,ak (не обязательно различных) называется маршрутом длины k, если граничные точки двух соседних ребер последовательности совпадают.Маршрут называется замкнутым, если его начальная и конечнаявершины совпадают. В противном случае маршрут незамкнутый. Цепь - незамкнутый маршрут, состоящий из последовательности различных ребер. Простая цепь - маршрут, который не проходит дважды через одну и ту же вершину. Цикл - замкнутый маршрут, состоящий из последовательности различных ребер. Простой цикл - маршрут, в котором начальная и конечная вершины совпадают, а все остальные вершины различны.

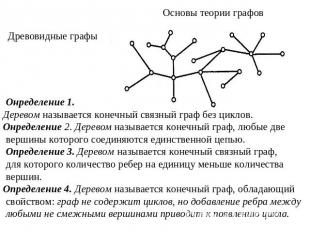
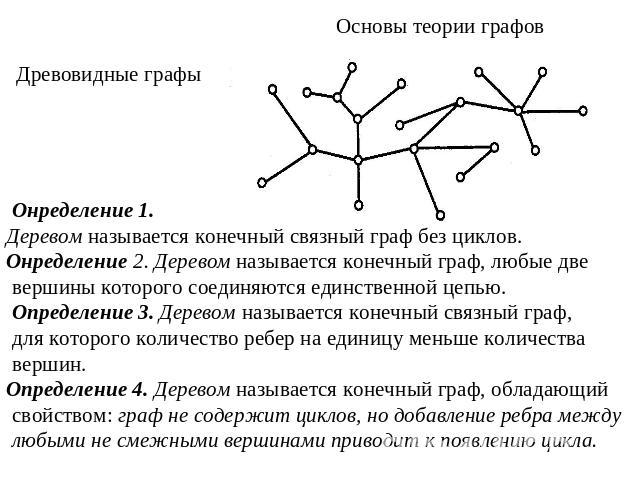
Основы теории графовДревовидные графы Онределение 1. Деревом называется конечный связный граф без циклов.Онределение 2. Деревом называется конечный граф, любые две вершины которого соединяются единственной цепью. Определение 3. Деревом называется конечный связный граф, для которого количество ребер на единицу меньше количества вершин. Определение 4. Деревом называется конечный граф, обладающий свойством: граф не содержит циклов, но добавление ребра между любыми не смежными вершинами приводит к появлению цикла.

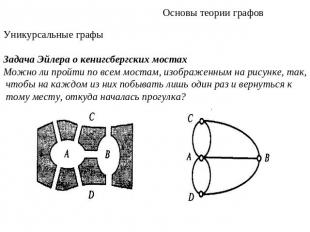
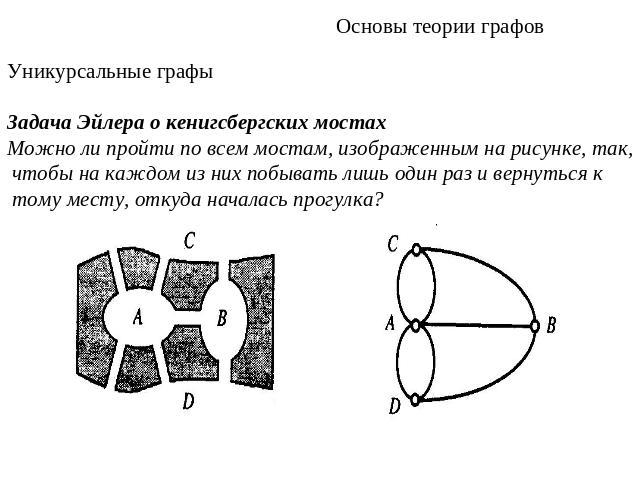
Основы теории графовУникурсальные графыЗадача Эйлера о кенигсбергских мостахМожно ли пройти по всем мостам, изображенным на рисунке, так, чтобы на каждом из них побывать лишь один раз и вернуться к тому месту, откуда началась прогулка?

Основы теории графовУникурсальные графыГраф называется уникурсальным графом (или эйлеровой линией), если все его ребра можно включить либо в простой цикл, либо в простую цепь.Признаки уникурсальных графов:Лемма. Если связный граф имеет более двух нечетных вершин, то он не уникурсален.Теорема 1. Связный граф является эйлеровым циклом тогда и только тогда, когда он имеет только четные вершины. При этом начало и конец уникурсального пути совпадают и могут находиться в любой вершине графа. Теорема 2. Связный граф является эйлеровой цепью тогда и только тогда, когда он имеет ровно две нечетные вершины, а остальныевершины этого графа четны. При этом начало и конец уникурсального пути находятся в нечетных вершинах.

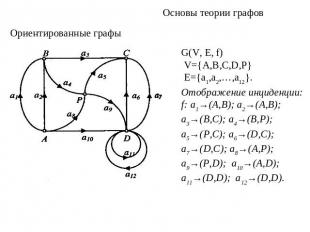
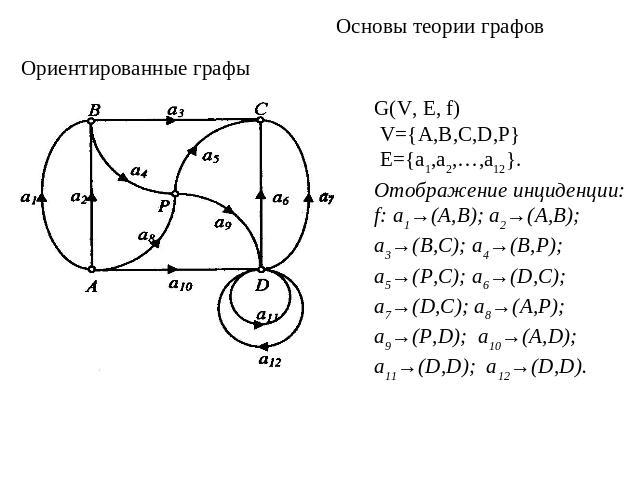
Основы теории графовОриентированные графыG(V, Е, f) V={A,В,С,D,Р} E={a1,a2,…,a12}. Отображение инциденции:f: a1→(A,B); a2→(A,B); a3→(B,C); a4→(B,P); a5→(P,C); a6→(D,C); a7→(D,C); a8→(A,P);a9→(P,D); a10→(A,D); a11→(D,D); a12→(D,D).

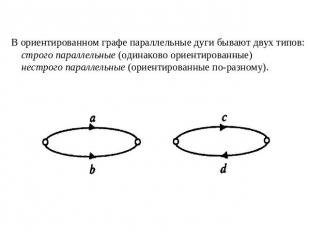
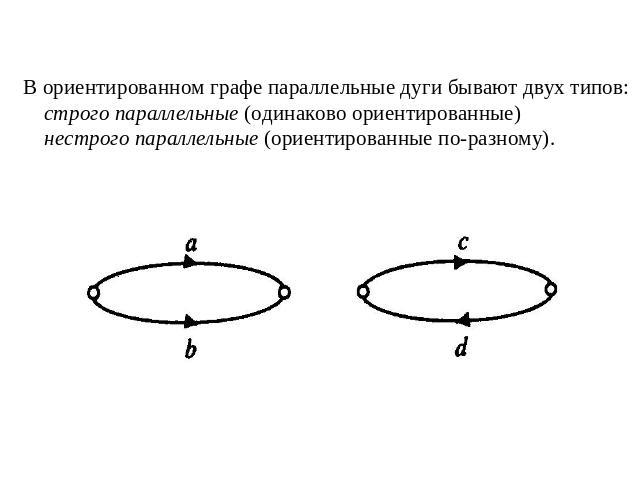
В ориентированном графе параллельные дуги бывают двух типов: строго параллельные (одинаково ориентированные) нестрого параллельные (ориентированные по-разному).

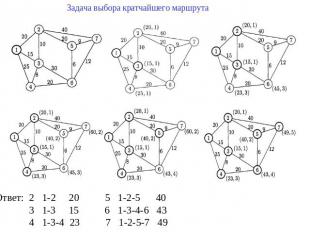
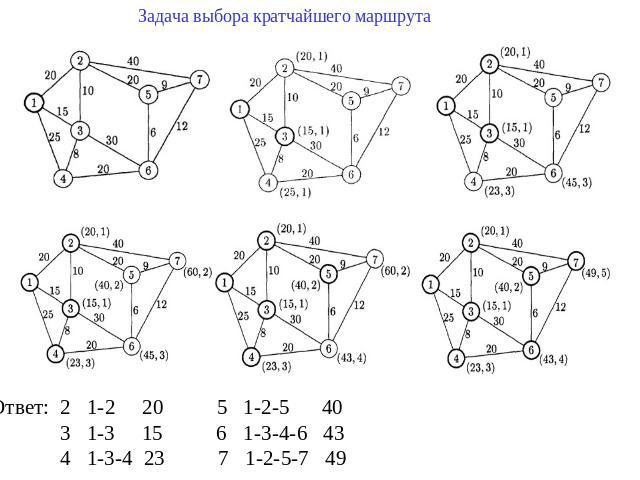
Задача выбора кратчайшего маршрута

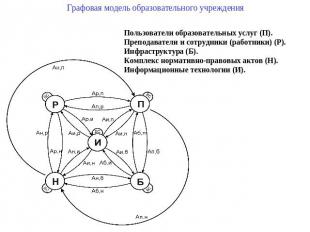
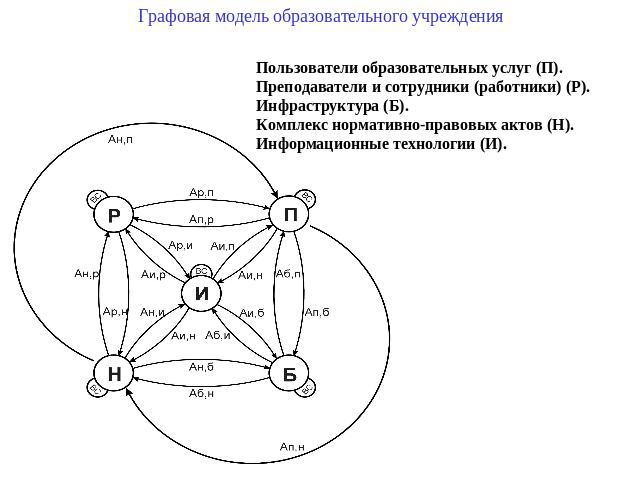
Графовая модель образовательного учреждения Пользователи образовательных услуг (П). Преподаватели и сотрудники (работники) (Р). Инфраструктура (Б). Комплекс нормативно-правовых актов (Н). Информационные технологии (И).