Презентация на тему: Графический метод решения ЗЛП

Рассмотрим ЗЛП на плоскости. при ограничениях

Каждое неравенство системы ограничений геометрически определяет полуплоскость с граничными прямыми Условия неотрицательности определяют полуплоскости с граничными прямыми Если система ограничений совместна, то область ее решения есть множество точек, принадлежащих всем указанным полуплоскостям. Совокупность этих точек называют многоугольником решений. Или областью допустимых решений (ОДР) ЗЛП.

Опр. Множество точек называется выпуклым, если вместе с любыми двумя точками оно содержит и весь отрезок. Тогда ОДР может быть вида: Выпуклый многоугольник; Выпуклая многоугольная неограниченная область; Пустая область; Отрезок; Единственная точка.

Целевая функция определяет на плоскости семейство прямых, одна из которых проходит через начало координат. Эта прямая называется основной. Прямая эта перпендикулярна нормальному вектору . Этот вектор указывает направление наискорейшего возрастания функции, а противоположный ему –направление наискорейшего убывания. Так что это вектор вида

Прямая , перпендикулярная градиенту, является линией уровня целевой функции и поэтому во всех своих точках принимает одно и тоже значение. Приравнивая целевую функцию к постоянной , а затем меняя ее, получим семейство прямых, каждая из которых является линией уровня, которые обладают свойством: при смещении в одну сторону уровень только возрастает, а в другую- только убывает.

Геометрическая интерпретация ЗЛП: Среди множества решений, которые находятся в многоугольнике решений, следует отыскать точку многоугольника, координаты которой обращают в максимум или минимум целевую функцию. Теорема. Если ЗЛП имеет оптимальный план, то целевая функция принимает свое оптимальное значение в одной из вершин многоугольника решений.

Для определения этой вершины строится основная прямая , которую перемещают в направлении градиента до тех пор, пока она не коснется последней крайней точки многоугольника решений. Это может быть вершина многоугольника, координаты которой и определяют максимальное значение целевой функции. Может быть и такой случай, когда последняя точка лежит на стороне многоугольника, и тогда целевая функция принимает максимальное значение на всей этой прямой. Если же в направлении градиента многоугольник решений неограничен, то .

Графический метод решения ЗЛП Нахождение решения ЗЛП на основе ее геометрической интерпретации включает следующие этапы: 1).Строят прямые, уравнения которых получаются в результате замены в ограничениях задачи знаков неравенств на знаки равенств. 2).Находят полуплоскости, определяемые из ограничений задачи. 3).Находят многоугольник решений. 4). Строят вектор . 5). Строят прямую , проходящую через многоугольник решений. 6).Передвигают эту прямую в направлении градиента. 7)Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Пример. Задача о костюмах. Намечается выпуск двух видов костюмов - мужских и женских.. На женский костюм требуется 1м шерсти, 2м полиэстера и 1человеко-день трудозатрат. На мужской –3,5м шерсти, 0,5м полиэстера и 1 человеко-день трудозатрат. Всего имеется 350м шерсти, 240 м полиэстера и150 человекодней трудозатрат.

Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского-20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

Решение. Обозначим: -число женских и число мужских костюмов соответственно. Целевая функция . Ограничения

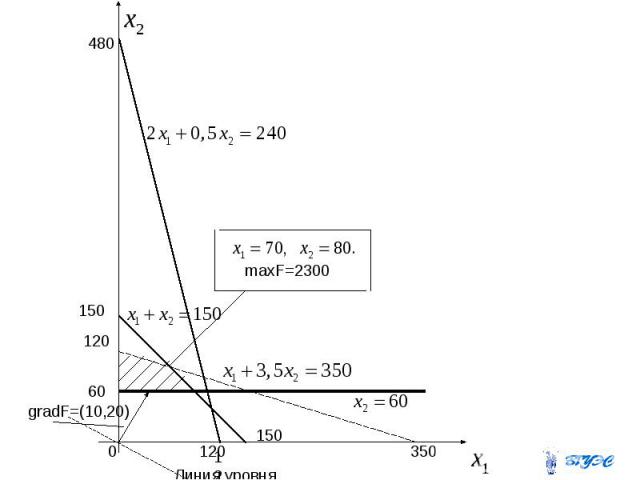
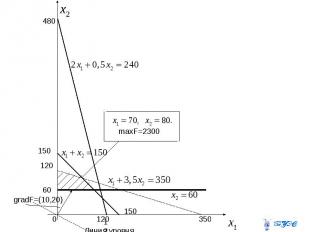
Построим прямые Первая прямая пересекает оси координат в точках (350;0) и (0;100), вторая – в точках (120;0) и (0;0;480), третья – в точках (150;0) и (0;150).Четвертая прямая проходит параллельно оси .

Строим все прямые и получаем четырехугольник, все точки которого удовлетворяют всем четырем функциональным ограничениям. Легко проверить: например, т.(0;0) лежит ниже всех трех первых прямых, но не удовлетворяет последнему соотношению. Так что, все точки внутри многоугольника удовлетворяют всем четырем неравенствам. Теперь построим градиент целевой функции (10;20). Для этого соединим точку (10,20) с началом координат. Можно построить вектор, пропорциональный этому вектору, т.е. длиннее или короче в зависимости от масштаба

Затем перпендикулярно ему основную прямую и будем перемещать ее в направлении градиента до ее выхода из ОДР. Это произойдет в точке пересечения прямых

Решим систему двух уравнений и получим точку При этих значениях

Пример Найти максимум и минимум функции при ограничениях

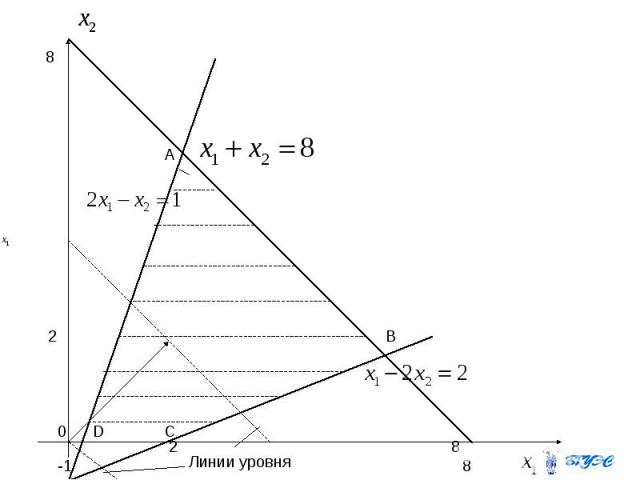
Решение. Строим многоугольник решений. Для этого изобразим прямые Первая из них проходит через токчи (8;0) и (0;8), вторая – через точки (0,5;0) и (0;-1), третья –через точки (2;0) и (0;-1). Далее изобразим градиент (3;3) и линии уровня.

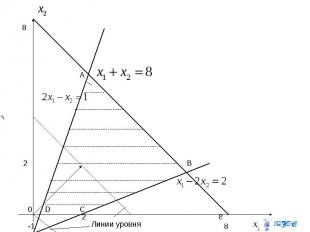
Передвигая линию уровня в направлении возрастания , т.е. в направлении градиента, получаем, что целевая функция достигает максимального значения вдоль прямой На прямой возьмем точку , например В, координаты которой можно найти из системы уравнений Целевая функция здесь имеет значение

При решении данной задачи на минимум целевой функции линию уровня следует двигать в направлении, обратном направлению градиента. Целевая функция достигает минимума в точке D пересечения прямой с осью , т.е. в точке ((0,5;0). Тогда

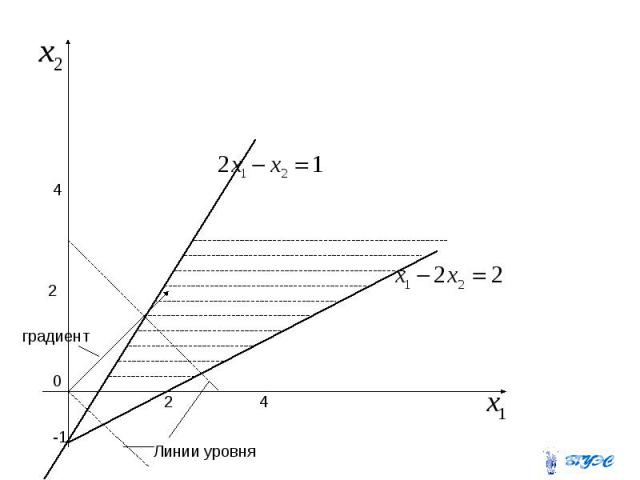
Пример. Найти максимум функции при ограничениях

Эта задача не имеет решения, т.к. целевая функция не ограничена сверху на ОДР. Это означает, что

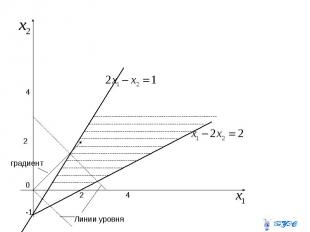
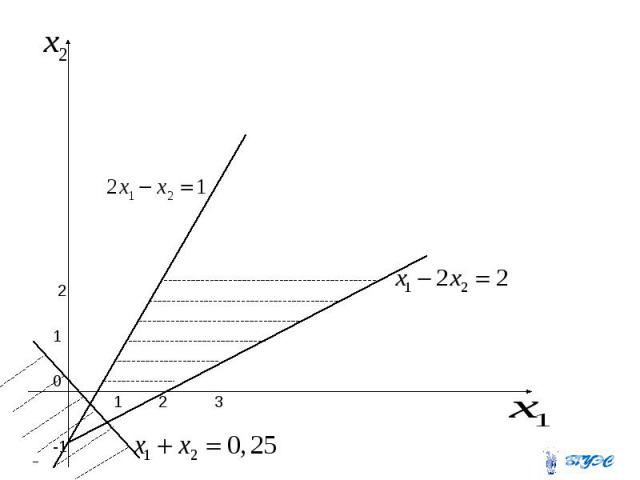
Найти максимум функции при ограничениях

Строим прямые, заменив знаки неравенств на знаки равенства, а затем закрасим область допустимых решений. Очевидно, начало координат находится ниже прямой , не удовлетворяет второму неравенству , поэтому точки области лежат правее этой прямой. Последнему неравенству удовлетворяет и поэтому получаем область на рисунке

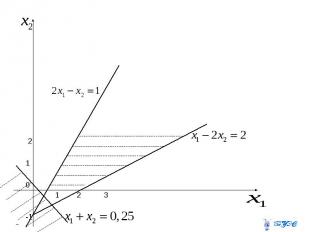
Из рисунка видим, что множество планов пусто, т.к.закрашенные области не имеют общих точек.