![Определённый интеграл с переменным верхним пределом Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл: где](https://fs1.ppt4web.ru/images/91944/111855/640/img19.jpg "Определённый интеграл с переменным верхним пределом Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл: где")
Презентация на тему: определенный интеграл
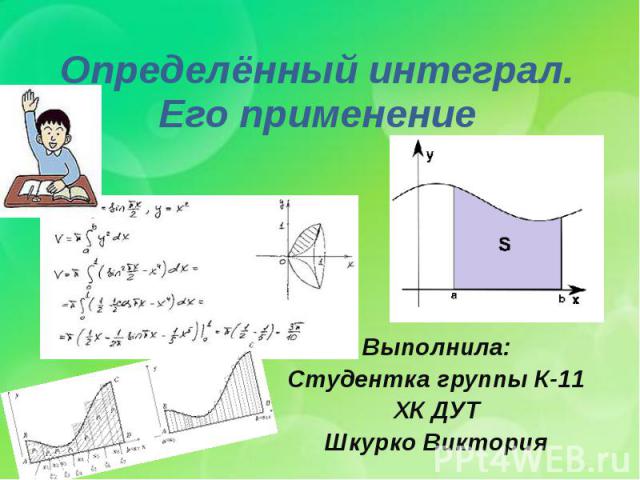
Определённый интеграл. Его применение Выполнила: Студентка группы К-11 ХК ДУТ Шкурко Виктория
План
Понятие определённого интеграла
Отрезок интегрирования
формулой Ньютона-Лейбница.
a=b
Разность F(b)- F(a)
Запись формулы Ньютона- Лейбница
Пример
Найдём новые пределы интегрирования.
Свойства определённого интеграла Т
Теорема 2
Теорема 3
Теорема 4.
Теорема 5
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е. Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е. Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е.
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство можно почленно интегрировать, т.е.
Определённый интеграл с переменным верхним пределом Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл: где
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
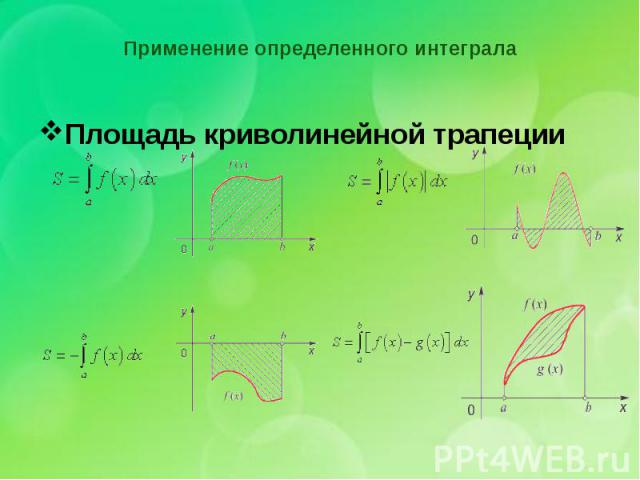
Применение определенного интеграла Площадь криволинейной трапеции
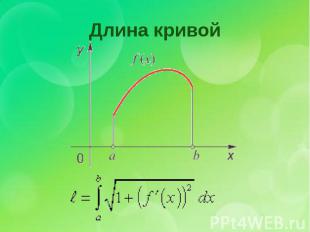
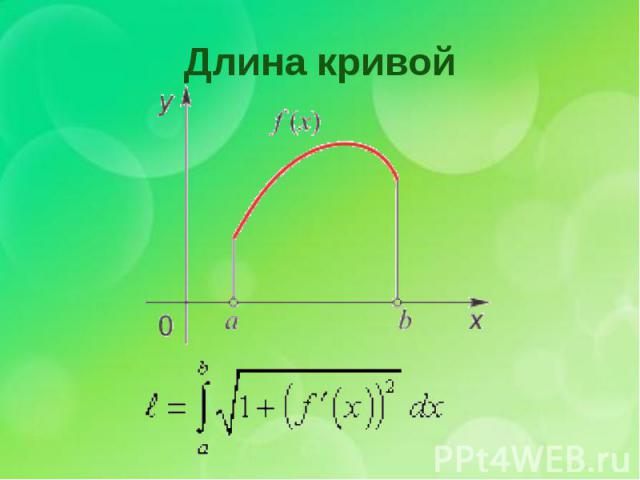
Длина кривой
Площадь поверхности вращения
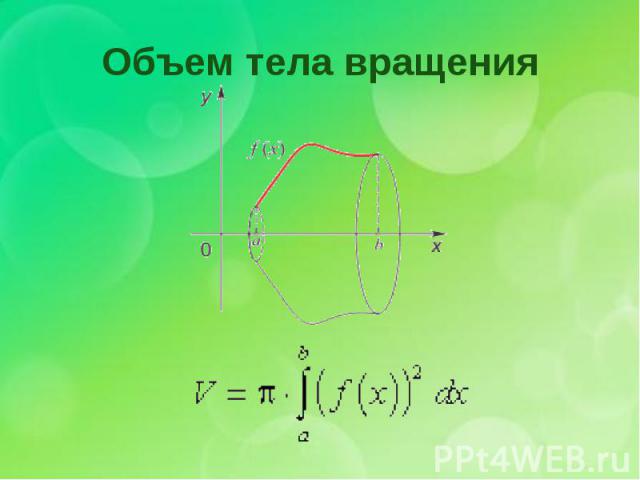
Объем тела вращения
Источники информации: http://function-x.ru/integral4.html Конспект лекций http://uztest.ru/abstracts/?idabstract=68542 http://osiktakan.ru/alg10.html
