Презентация на тему: Понятие осевой симметрии

900igr.net

Определение и теорема Примеры Задачи

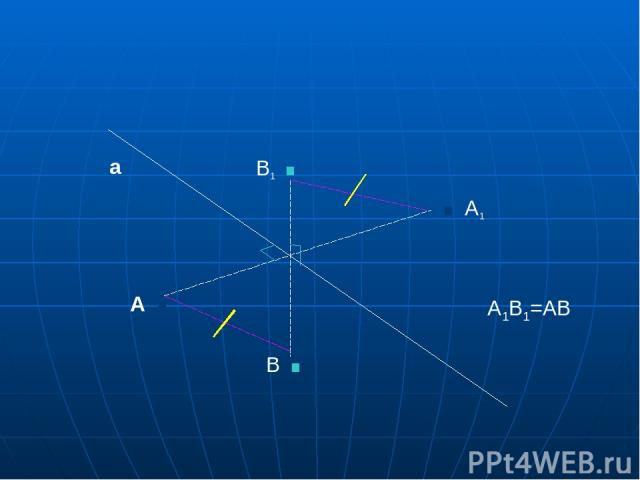
Осевой симметрией с осью a называется такое отображение пространства на себя , при котором любая точка М переходит в симметричную ей точку М1 относительно оси а. . М а . М1

Под движением пространства понимается отображение пространства на себя , при котором любые две точки А и В переходят в какие-то точки А1 и В1 так , что А1В1=АВ. Движение пространства - это отображение пространства на себя ,сохраняющее расстояние между точками.

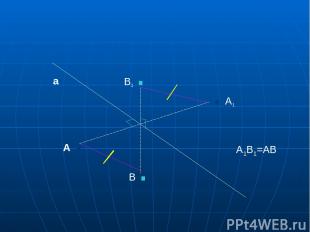
А . . А1 В1 . В . а А1В1=АВ

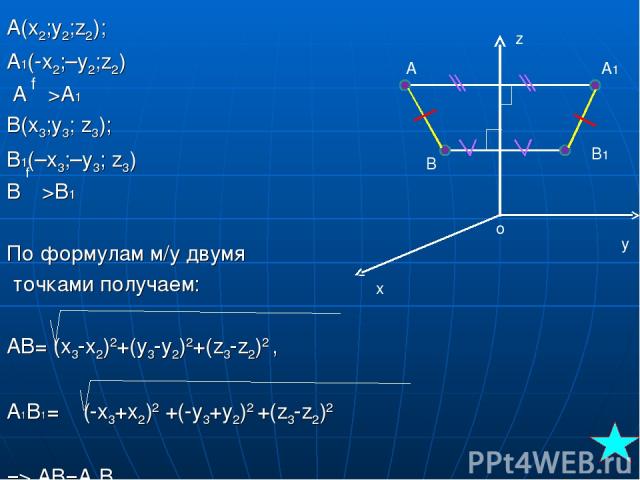
Теорема № 1 Дано:f―осевая симметрия; А―>А1; В―>В1;М―>М1; М(x;y;z), М1(x1;y1;z1); А(x2;y2;z2); B(x3;y3;z3) До-ть:что осевая симметрия является движением. (AB=A1B1) Решение: Если М не принадлежит OZ ,то ось OZ: 1)проходит через середину отрезка ММ1. 2)перпендикулярна к нему. Из 1усл.по формулам получаем (x+x1)/2 и (y+y1)/2 , откуда x1=-x и y1=-y. Из усл. №2 :z1=z. Полученные формулы равны если т-а М лежит на оси Oz.

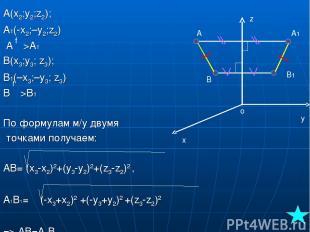
A(x2;y2;z2); A1(-x2;–y2;z2) A―>A1 B(x3;y3; z3); B1(–x3;–y3; z3) B―>B1 По формулам м/у двумя точками получаем: AB= (x3-x2)2+(y3-y2)2+(z3-z2)2 , A1B1= (-x3+x2)2 +(-y3+y2)2 +(z3-z2)2 => AB=A1B1 A A1 B B1 z x y o f f

ПРИМЕР Треугольник Ромб Квадрат Сложные примеры Равнобедренный треугольник Круг

НАЗАД

НАЗАД

НАЗАД

НАЗАД

НАЗАД

Найдите координаты точек, в которые переходят точки А(0;1;2) , В(3;-1;4) , С(1;0;-2) при: осевой симметрии относительно координатных осей.

Дано: А(0;1;2) , В(3;-1;4) , С(1;0;-2) Найти:А1 , В1 ,С1 Решение : Выберим произвольную ось симметрии Oz.Если т-и не лежат на оси симметрии ,то ось Oz проходит ч/з середину отрезка АА1 , ВВ1 и СС1 к ним => x1=-x и y1=-y и z1=z => А(0;-1;2), В(-3;1;4), С(-1;0;-2) Ответ: А(0;-1;2), В(-3;1;4), С(-1;0;-2)

Докажите, что при осевой симметрии плоскости прямая, параллельная оси симметрии, отображается на прямую, параллелью оси симметрии

Дано: l – ось симметрии, а║l, Доказать: b║ l Доказательство: Если а II l, то симметричная прямая b тоже II l, при осевой симметрии сохраняется расстояние между точками: АА1 перпендикулярно l; BB1 перпендикулярно l, следовательно b II a; Так как a II l; a II b, то есть b II l. ч.т. д. НАЗАД