Презентация на тему: Понятие движения

9 класс геометрия «Движение» 5klass.net

Понятие движения.

Цели урока: Рассмотреть осевую и центральную симметрии. Ввести понятие отображения плоскости на себя и движения.

Повторение. Осевая симметрия. Постройте точки симметричные А и В относительно прямой l. l A В А1 В1 А В А2
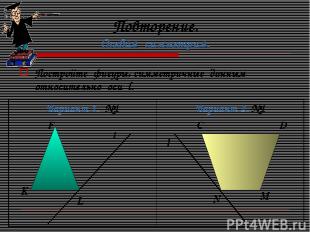
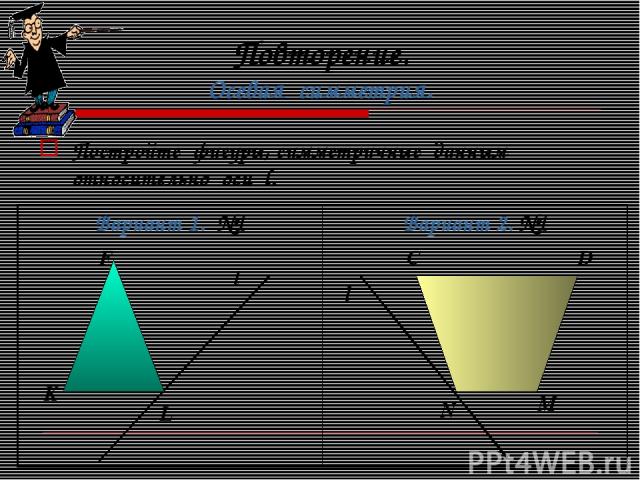
Повторение. Осевая симметрия. Постройте фигуры, симметричные данным относительно оси l. l F K L l C D N M Вариант 1. №1 Вариант 2. №1

Ответьте на вопросы: В какую фигуру отобразился треугольник? В какую фигуру отобразилась трапеция? Сохранилось ли расстояние между точками?
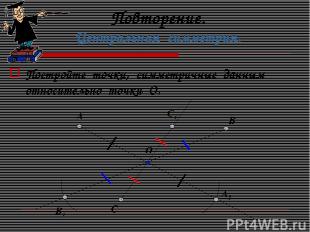
Повторение. Центральная симметрия. Постройте точки, симметричные данным относительно точки О. О А В С А1 В1 С1
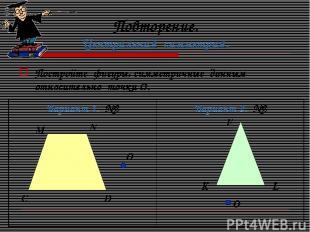
Повторение. Центральная симметрия. Постройте фигуры, симметричные данным относительно точки О. F K L C D N M О О Вариант 1. №2 Вариант 2. №2

Ответьте на вопросы: В какую фигуру отобразился треугольник? В какую фигуру отобразилась трапеция? Сохранилось ли расстояние между точками?

Найдите соответствия: Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Говорят, что дано отображение плоскости на себя. (Осевая и центральная симметрии) Отображение плоскости на себя, сохраняющее расстояние, называют движением
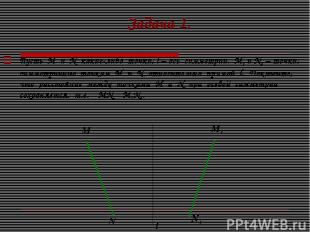
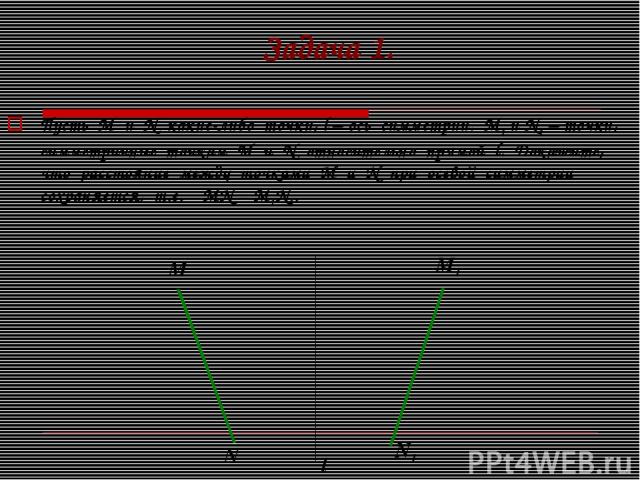
Задача 1. Пусть М и N какие-либо точки, l – ось симметрии. М1 и N1 – точки, симметричные точкам М и N относительно прямой l. Докажите, что расстояние между точками М и N при осевой симметрии сохраняется, т.е. МN = M1N1. l M N M1 N1

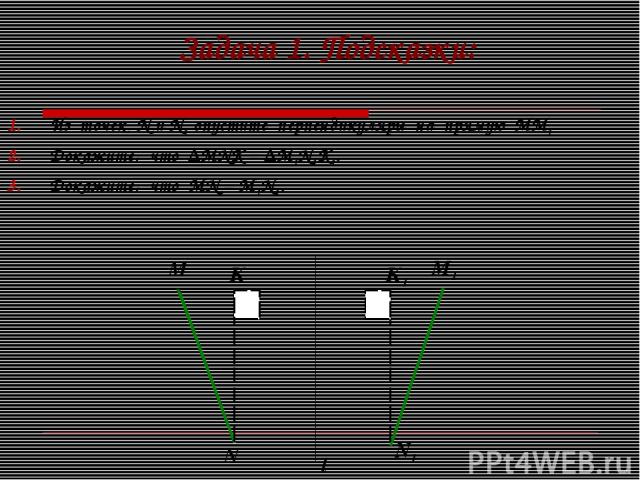
Задача 1. Подсказки: Из точек N и N1 опустите перпендикуляры на прямую ММ1 Докажите, что ∆MNK = ∆M1N1K1. Докажите, что МN = М1N1. l M N M1 N1 К К1

Задача 2. (№3) Докажите, что центральная симметрия есть движение. Подсказки: Возьмите точки М и N и О – центр симметрии. Постройте точки М1 и N1 относительно точки О. Докажите, что ∆ОМN = ∆OM1N1. Докажите, что МN = M1N1. Отображение плоскости на себя, сохраняющее расстояние, называют движением

Домашнее задание: Пп. 113, 114; №№ 1148, 1149.