Презентация на тему: понятие движения

ПОНЯТИЕ ДВИЖЕНИЯ

* ДВИЖЕНИЯ

* Движение – это жизнь!!!

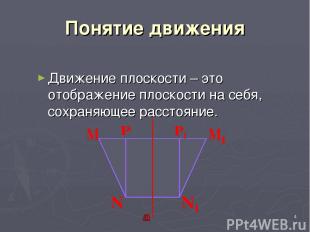
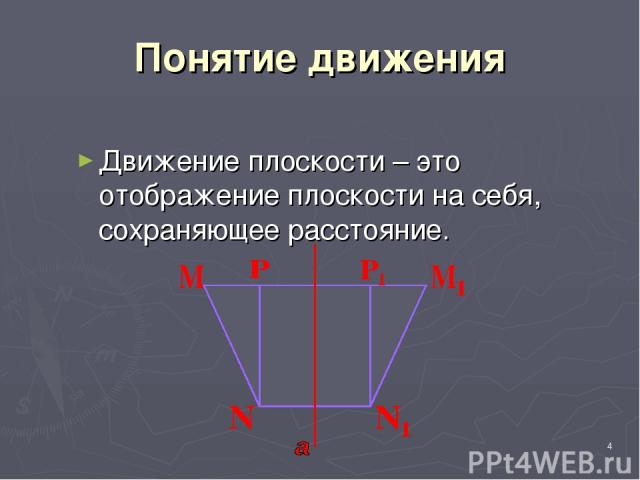
* Понятие движения Движение плоскости – это отображение плоскости на себя, сохраняющее расстояние.

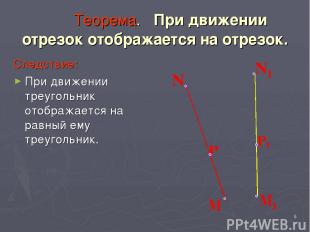
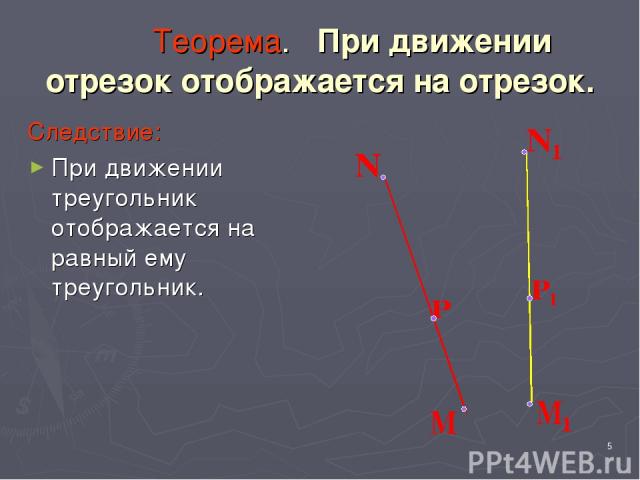
* Теорема. При движении отрезок отображается на отрезок. Следствие: При движении треугольник отображается на равный ему треугольник.

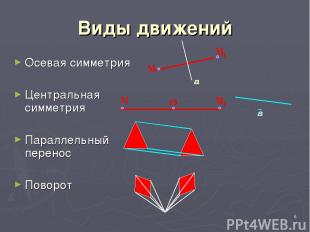
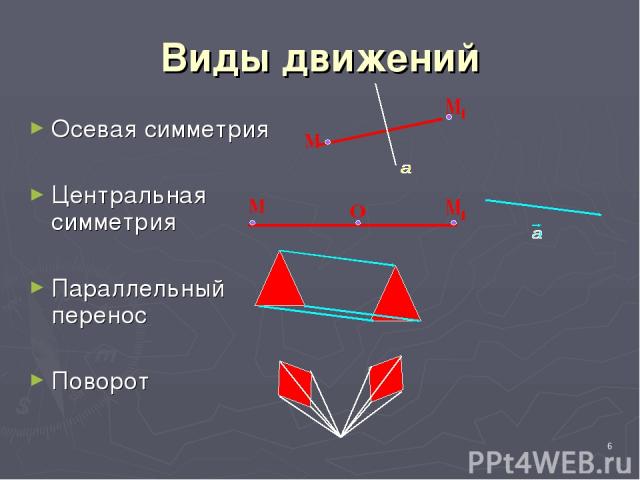
* Виды движений Осевая симметрия Центральная симметрия Параллельный перенос Поворот

Осевая симметрия Какие точки называются симметричными относительно данной прямой? Две точки А и А1 называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА1 и перпендикулярна ему. Как построить точку симметричную данной относительно прямой L? А L А1 А О А1 L

Центральная симметрия Какие точки называются симметричными относительно данной точки? Две точки А и А1 называются симметричными относительно точки, если эта точка является серединой отрезка АА1. Как построить точку симметричную данной относительно некоторой точки О? А О А1 А О А1

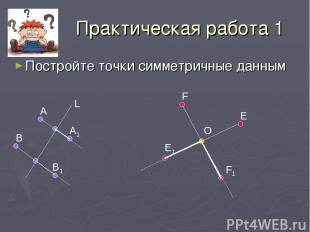
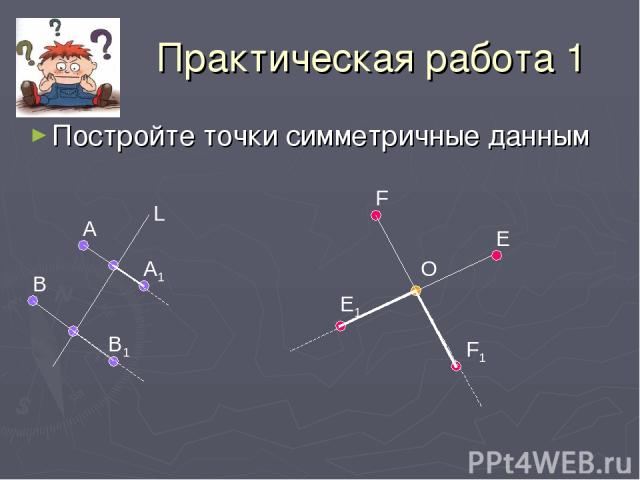
Практическая работа 1 Постройте точки симметричные данным А В А1 В1 L F E O E1 F1

Отображение плоскости на себя Пусть каждой точке плоскости ставится в соответствие какая –то точка этой плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.

Понятие движения Какими общими свойствами обладают осевая и центральная симметрия? Отображение плоскости на себя, сохраняющее расстояние, называют – движением.

Решение задач Решить задачу № 1153 (учебник)

Итог урока Осевая и центральная симметрия - движение. Д/з п.113,114 вопросы 1 -6 № 1148(а)