Презентация на тему: Аксиомы стереометрии 10 класс

Первые уроки геометрии в 10 классе

Аксиомы стереометрии Сформулируйте содержание аксиом А1, А2, А3, А4 Прокомментируйте их с помощью приведенных ниже рисунков. α С В А α В А α Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А, В, С одной прямой А, В, С α α - единственная плоскость Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. А, В α, АВ α Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В любой плоскости пространства справедливы все аксиомы и теоремы планиметрии. α - любая плоскость С α, β; α β = с; С с. Чертеж запись формулировка

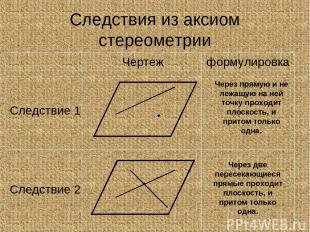
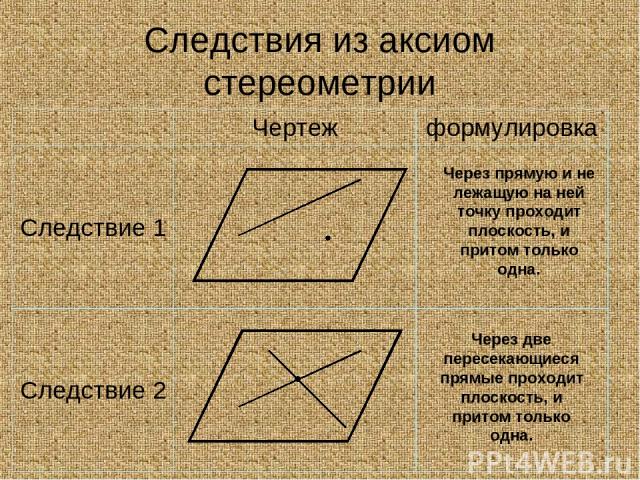
Следствия из аксиом стереометрии Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Через две пересекающиеся прямые проходит плоскость, и притом только одна. Чертеж формулировка Следствие 1 Следствие 2

Задача ABCD – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая на плоскости ромба. Точки A, D, O лежат на плоскости α. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями. 1. Лежат ли на плоскости α точки В и С? 2. Лежит ли на плоскости (МОВ) точка D? 3. Назовите линию пересечения плоскостей (МОВ) и (ADO). 4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 600. Назовите различные способы вычисления площади ромба.

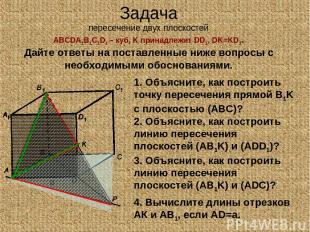
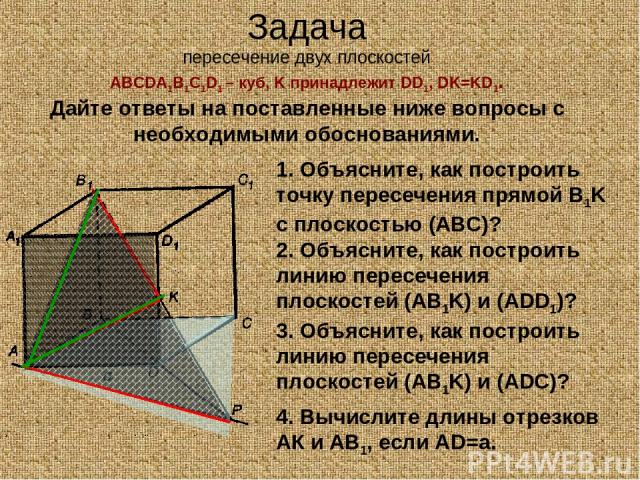
Задача пересечение двух плоскостей ABCDA1B1C1D1 – куб, K принадлежит DD1, DK=KD1. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями. 1. Объясните, как построить точку пересечения прямой B1K с плоскостью (АВС)? 2. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADD1)? 3. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADС)? 4. Вычислите длины отрезков АК и АВ1, если АD=a.

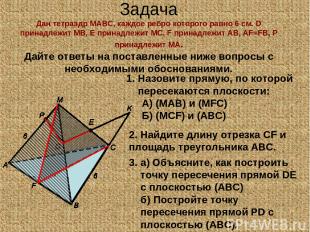
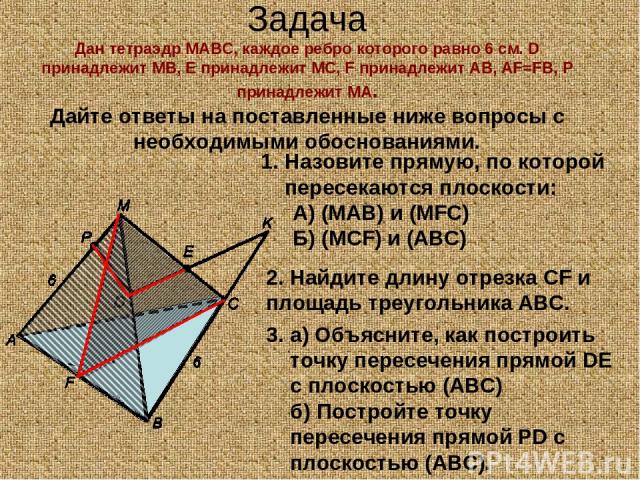
Задача Дан тетраэдр МАBC, каждое ребро которого равно 6 см. D принадлежит МВ, Е принадлежит МС, F принадлежит АВ, AF=FB, P принадлежит МА. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями. Назовите прямую, по которой пересекаются плоскости: А) (МАВ) и (MFC) Б) (MCF) и (АВС) 2. Найдите длину отрезка CF и площадь треугольника АВС. а) Объясните, как построить точку пересечения прямой DE с плоскостью (АВС) б) Постройте точку пересечения прямой PD с плоскостью (АВС).