Презентация на тему: N-угольники

5klass.net

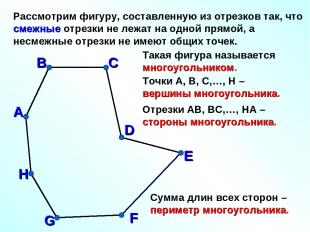
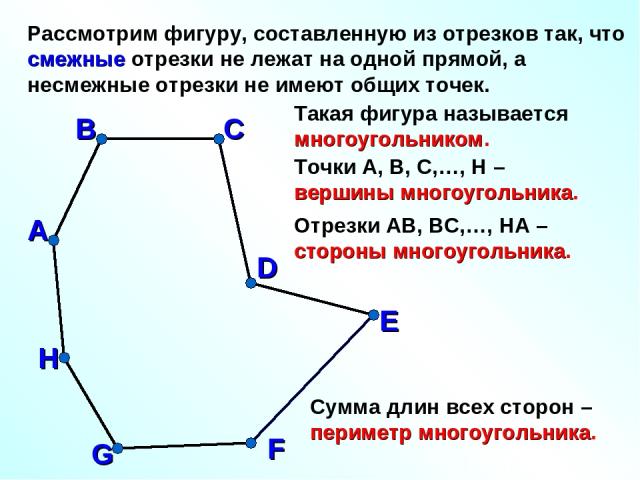
Рассмотрим фигуру, составленную из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек. А В С D E F G H Такая фигура называется многоугольником. Точки А, В, С,…, H – вершины многоугольника. Отрезки АВ, ВС,…, HА – стороны многоугольника. Сумма длин всех сторон – периметр многоугольника.

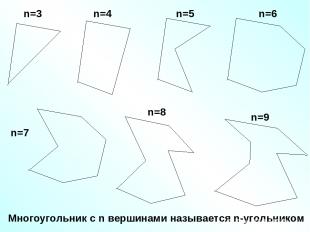
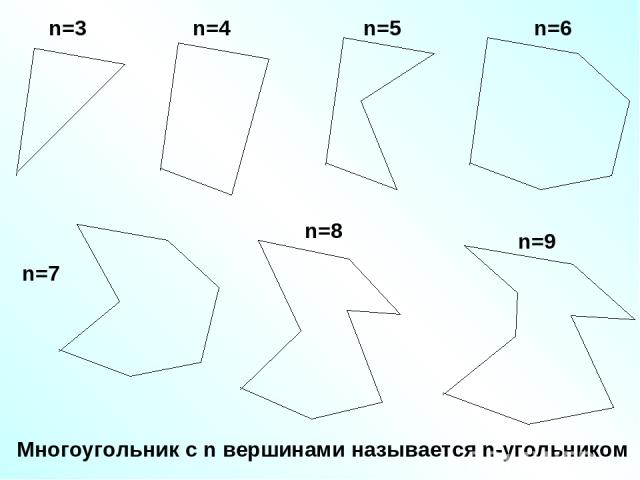
Многоугольник с n вершинами называется n-угольником n=3 n=4 n=5 n=6 n=7 n=8 n=9

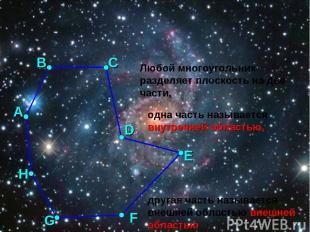
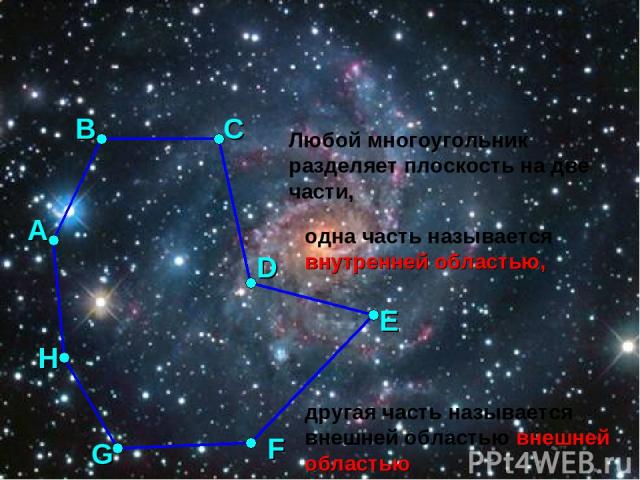
Любой многоугольник разделяет плоскость на две части, А В С D E F G H одна часть называется внутренней областью, другая часть называется внешней областью внешней областью

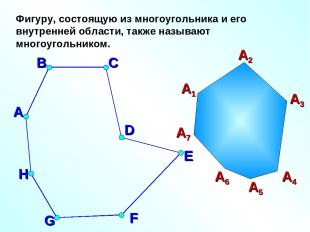
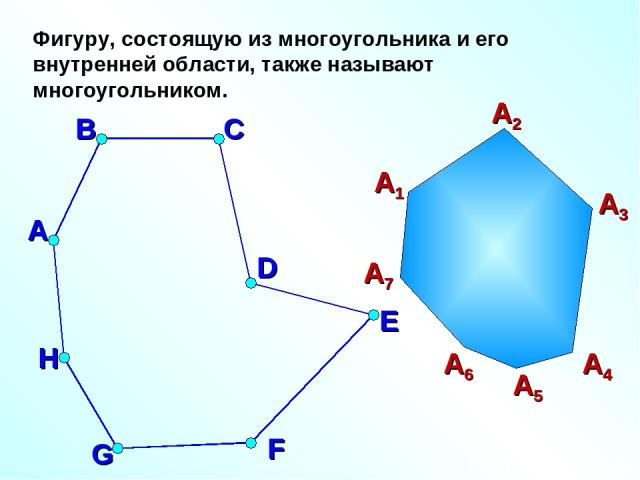
Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником. А В С D E F G H А1 А2 А3 А4 А5 А6 А7

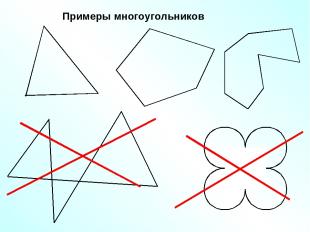
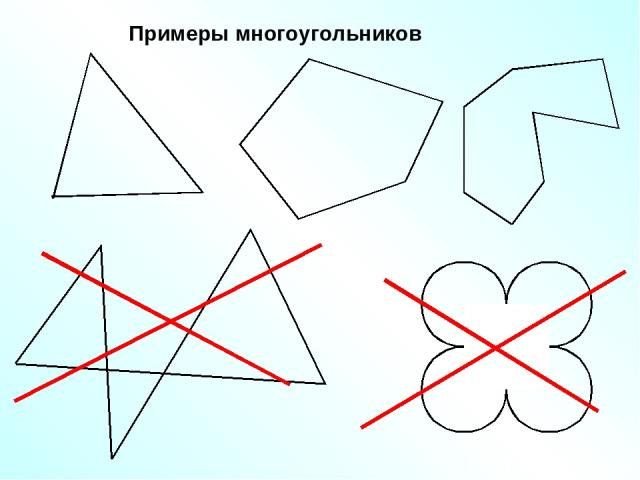
Примеры многоугольников

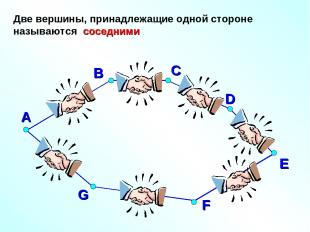
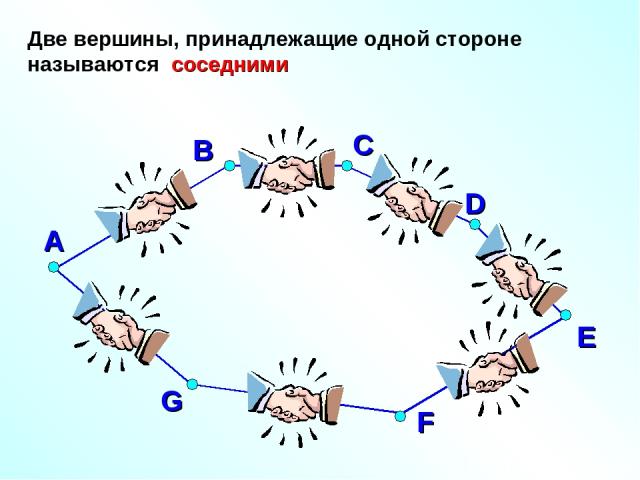
А В D E F G Две вершины, принадлежащие одной стороне называются соседними С

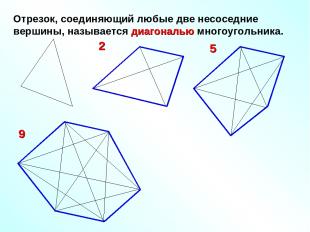
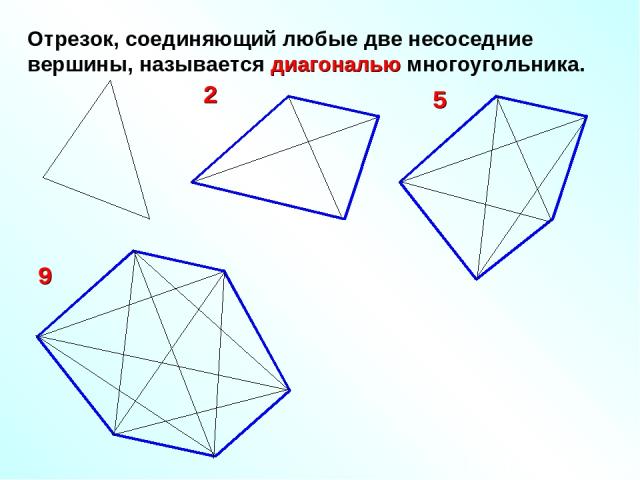
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника. 2 5 9

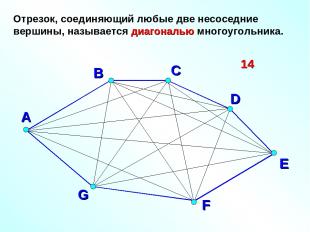
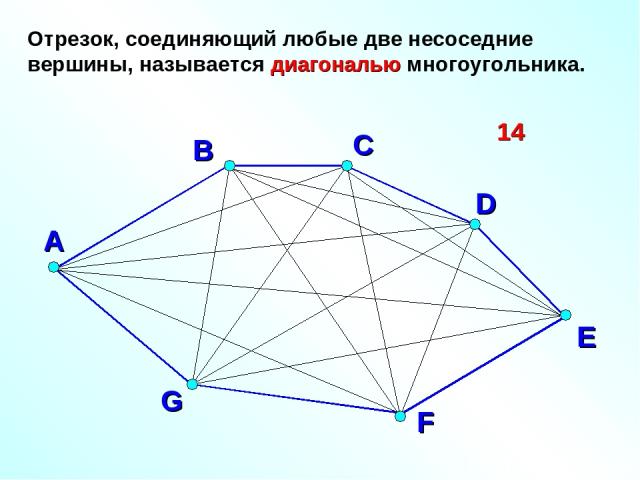
С А В D E F G Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника. 14

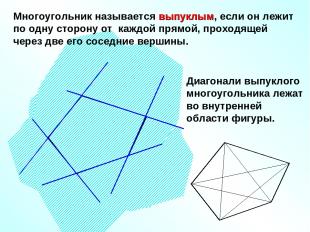
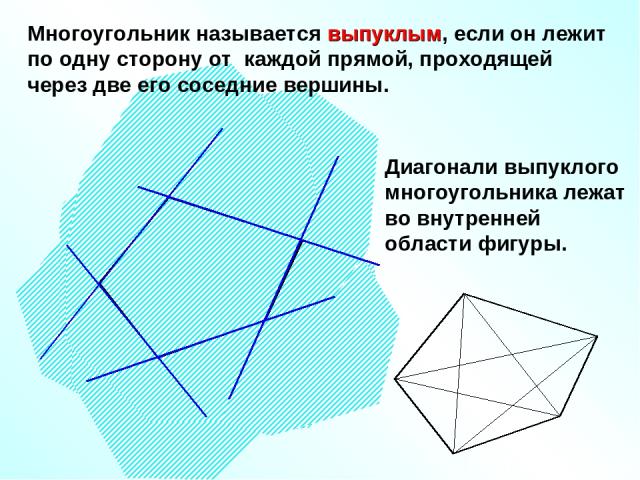
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Диагонали выпуклого многоугольника лежат во внутренней области фигуры.

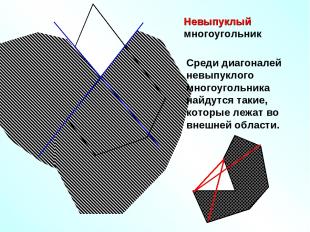
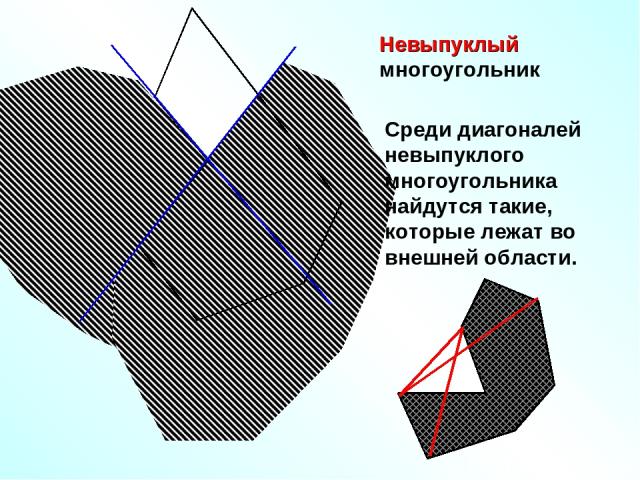
Невыпуклый многоугольник Среди диагоналей невыпуклого многоугольника найдутся такие, которые лежат во внешней области.

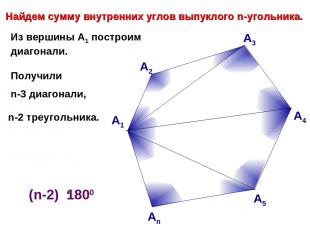
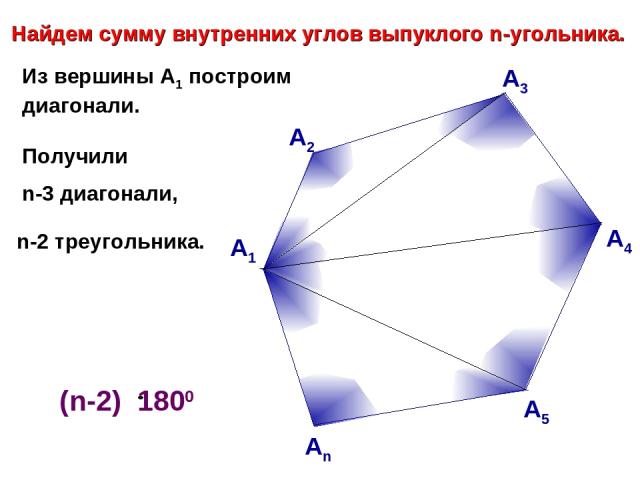
Из вершины А1 построим диагонали. Получили А1 Найдем сумму внутренних углов выпуклого n-угольника. А2 А3 А4 А5 Аn n-2 треугольника. n-3 диагонали,

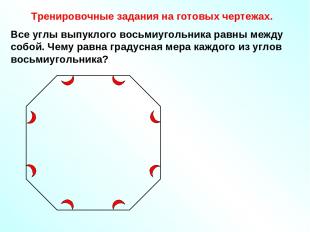
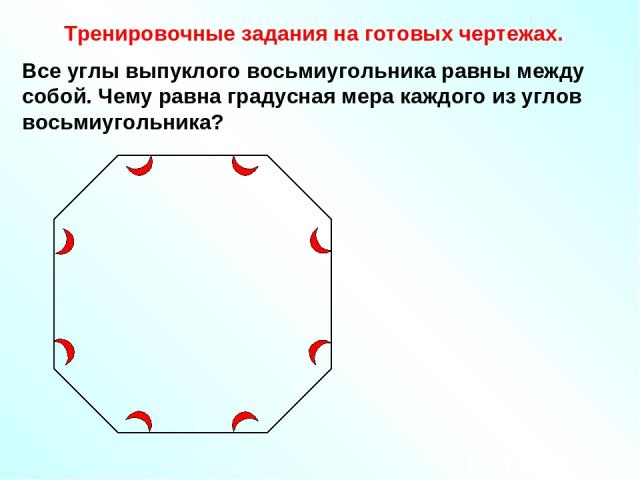
Тренировочные задания на готовых чертежах. Все углы выпуклого восьмиугольника равны между собой. Чему равна градусная мера каждого из углов восьмиугольника?

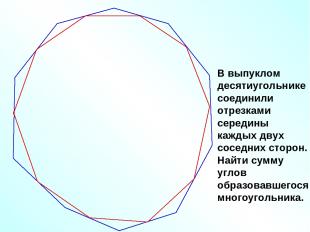
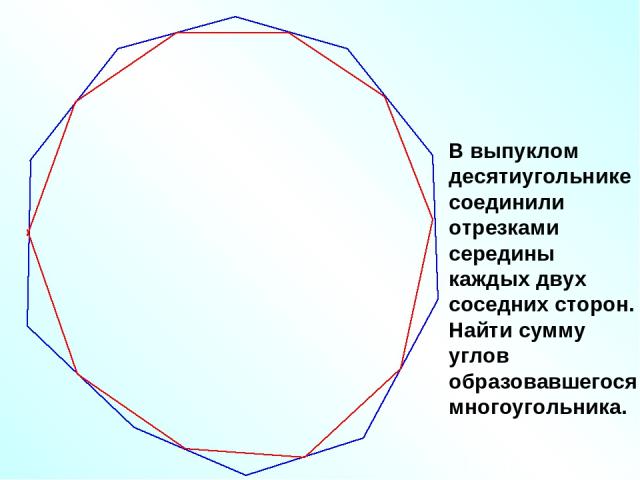
В выпуклом десятиугольнике соединили отрезками середины каждых двух соседних сторон. Найти сумму углов образовавшегося многоугольника.

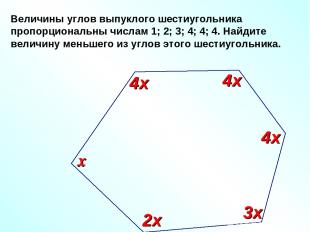
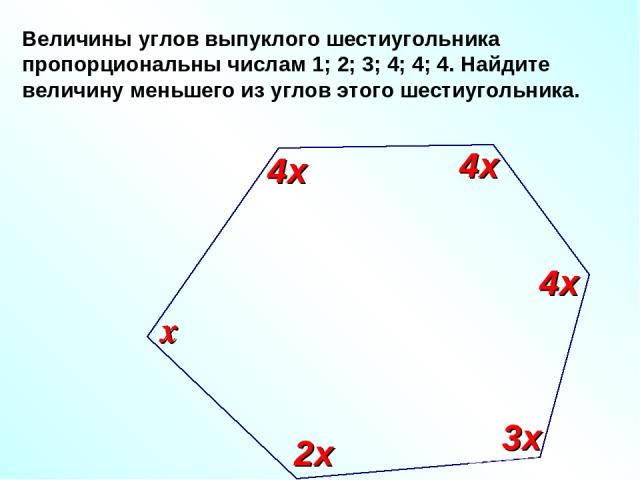
Величины углов выпуклого шестиугольника пропорциональны числам 1; 2; 3; 4; 4; 4. Найдите величину меньшего из углов этого шестиугольника. х 2х 3х 4х 4х 4х

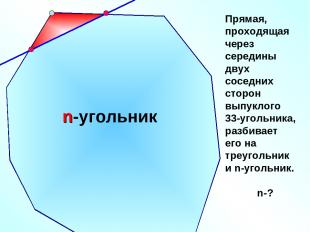
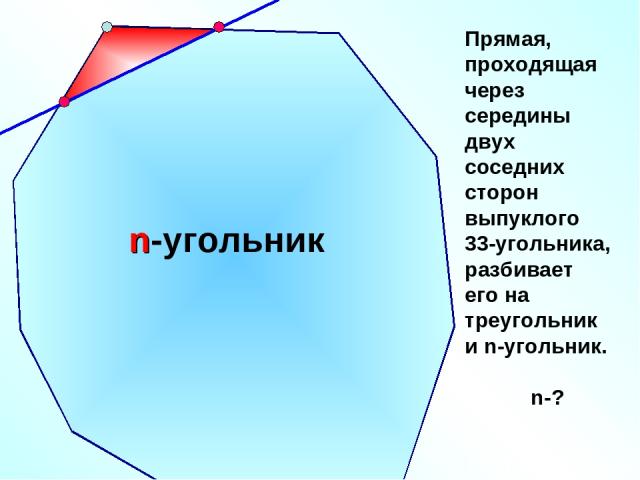
Прямая, проходящая через середины двух соседних сторон выпуклого 33-угольника, разбивает его на треугольник и n-угольник. n-? n-угольник

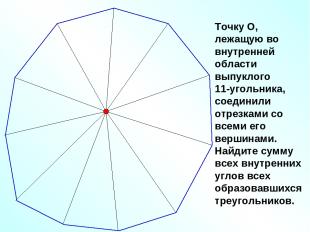
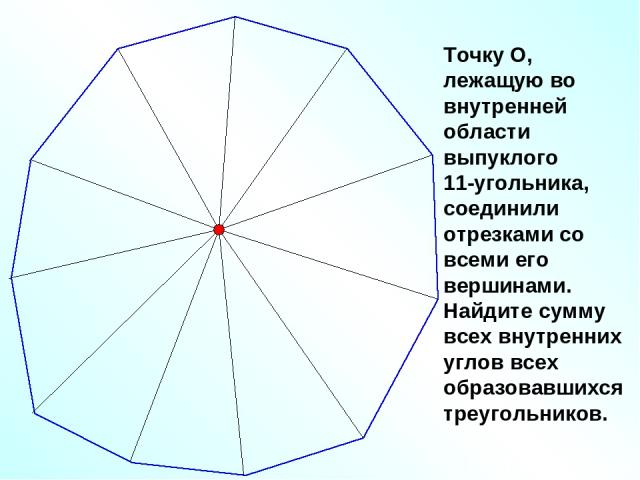
Точку О, лежащую во внутренней области выпуклого 11-угольника, соединили отрезками со всеми его вершинами. Найдите сумму всех внутренних углов всех образовавшихся треугольников.

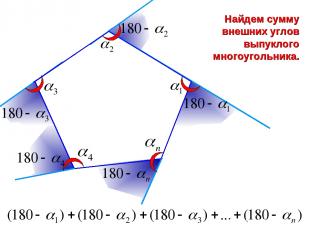
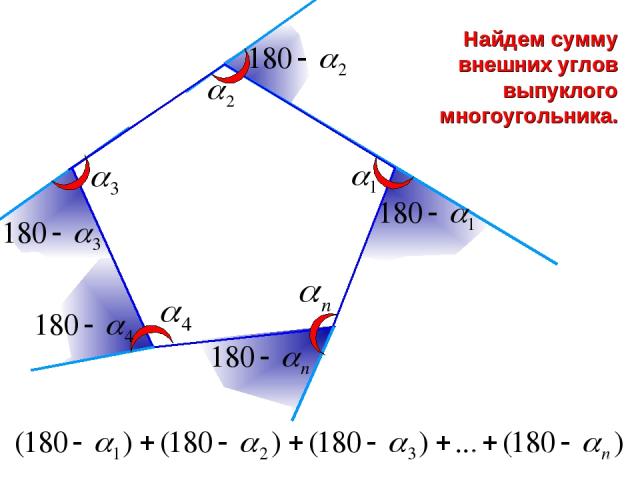
Найдем сумму внешних углов выпуклого многоугольника.

Выполним упрощение выражения = 3600 Сумма внешних углов выпуклого многоугольника.

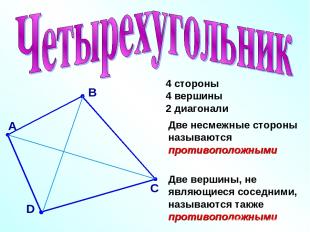
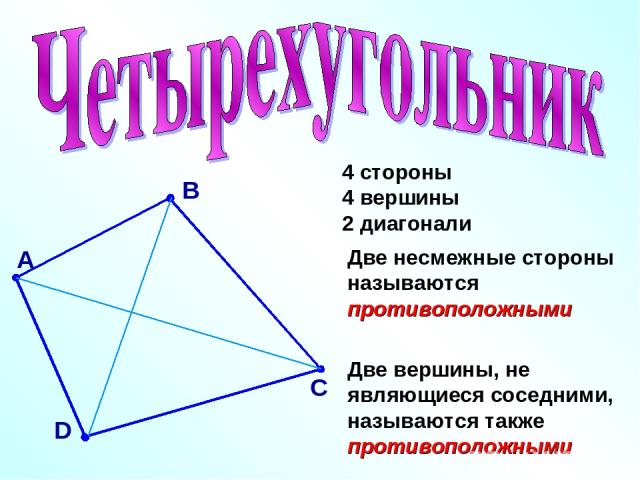
В А С D 4 стороны 4 вершины 2 диагонали Две несмежные стороны называются противоположными Две вершины, не являющиеся соседними, называются также противоположными

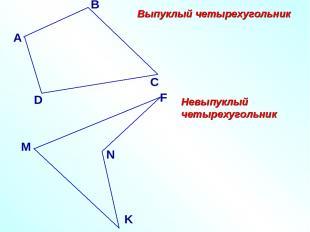
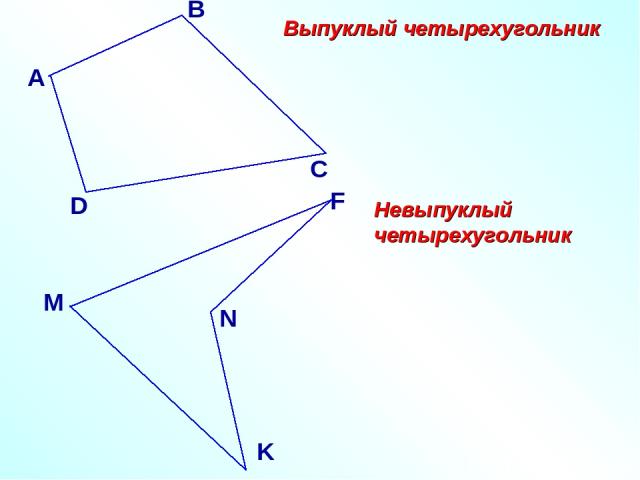
Выпуклый четырехугольник Невыпуклый четырехугольник

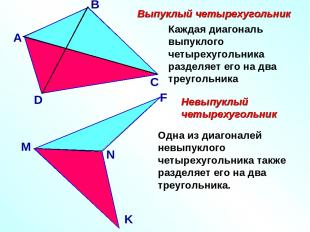
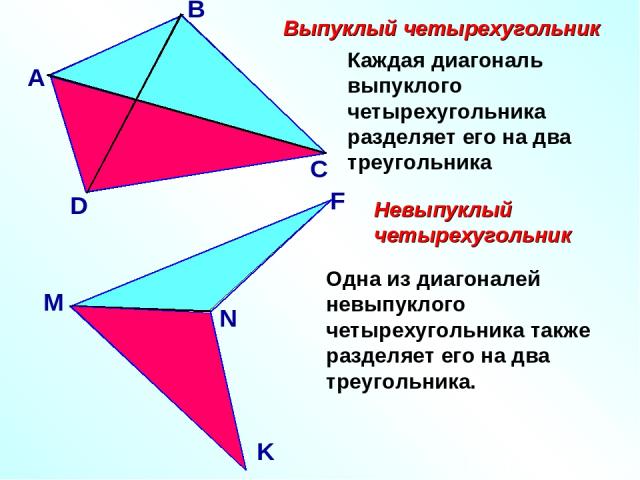
Выпуклый четырехугольник Невыпуклый четырехугольник Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника Одна из диагоналей невыпуклого четырехугольника также разделяет его на два треугольника.

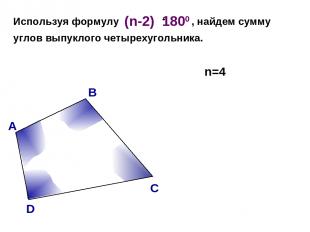
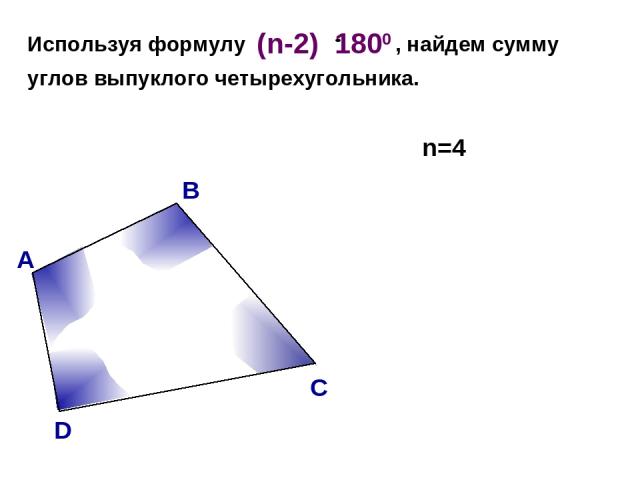
В А С D Используя формулу , найдем сумму углов выпуклого четырехугольника. n=4

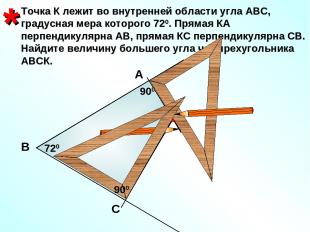
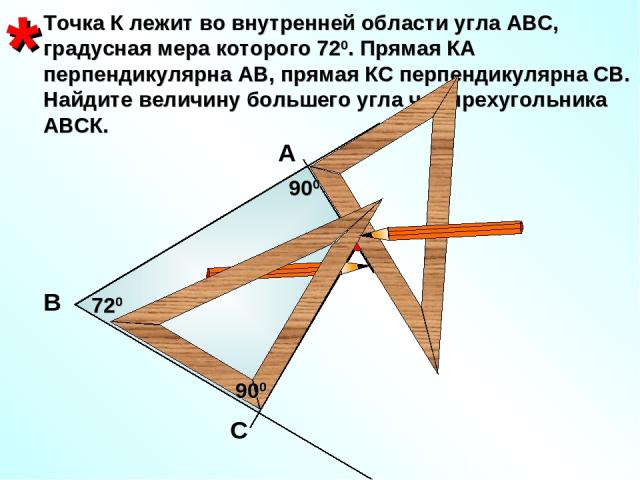
К Точка К лежит во внутренней области угла АВС, градусная мера которого 720. Прямая КА перпендикулярна АВ, прямая КС перпендикулярна СВ. Найдите величину большего угла четырехугольника АВСК. * А В С 720 900 900

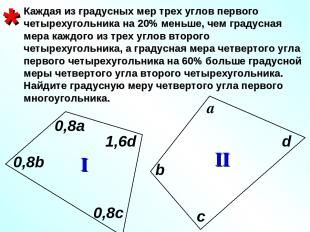
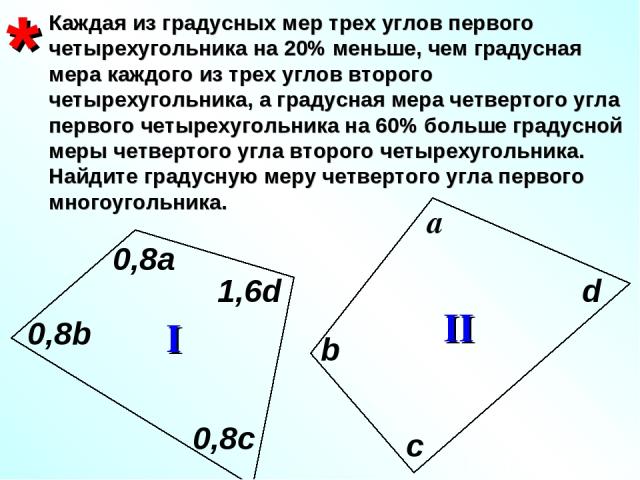
Каждая из градусных мер трех углов первого четырехугольника на 20% меньше, чем градусная мера каждого из трех углов второго четырехугольника, а градусная мера четвертого угла первого четырехугольника на 60% больше градусной меры четвертого угла второго четырехугольника. Найдите градусную меру четвертого угла первого многоугольника. * b I II а 0,8а 0,8b c 0,8c d 1,6d

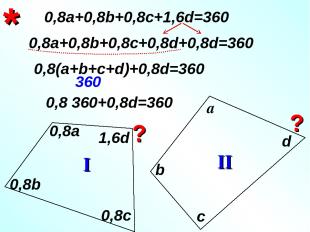
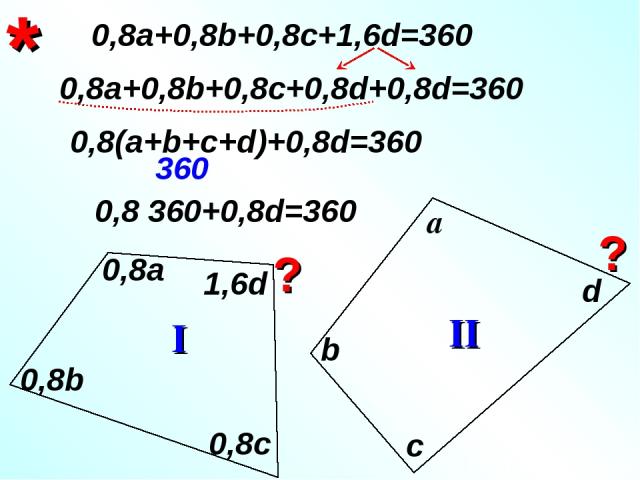
* b I II а 0,8а 0,8b c 0,8c d 1,6d 0,8а+0,8b+0,8c+1,6d=360 0,8а+0,8b+0,8c+0,8d+0,8d=360 0,8(а+b+c+d)+0,8d=360 ? ? 360