Презентация на тему: «Треугольники» 9 класс

Презентация по теме: «Треугольники» Подготовили Ученицы 9 класса Б Камаретдинова Карина Семёнова Алина 5klass.net

Треугольники Треугольники Треугольники

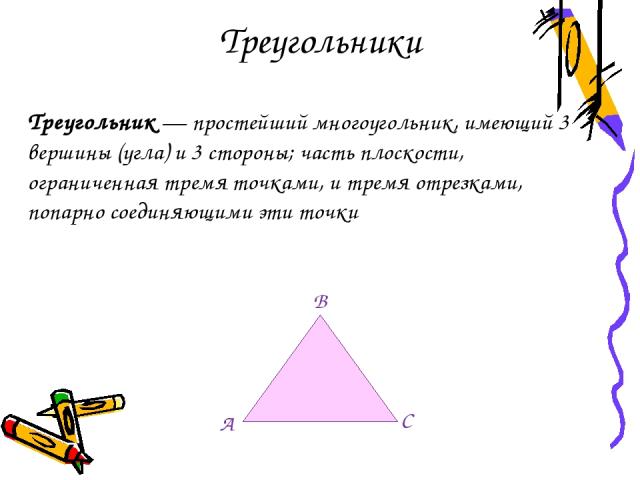
Треугольники Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки B

Равносторонний - это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°. Радиус вписанной окружности Радиус описанной окружности Периметр Высота Площадь

Равнобедренный Треугольник, в котором две стороны равны между собой называется равнобедренным. Равные стороны называются боковыми, а последняя - основанием Площадь треугольника Теорема косинусов Теорема синусов Периметр P = 2a + b (по определению); P = 2R(2sinα + sinβ) (следствие теоремы синусов)                                                                                                                                                                                                                М b

Прямоугольный Свойства: Сумма двух острых углов п/у треугольника равна 90°. Катет п/у треугольника, лежащий против угла в 30°, равен половине гипотенузы. Если катет п/у треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Признаки равенства п/у треугольников: Если катеты одного п/у треугольника соответственно равны катетам другого, то такие треугольники равны. Если катет и прилежащий к нему острый угол одного п/у треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Если гипотенуза и острый угол одного п/у треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны. Если гипотенуза и катет одного п/у треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. a2 + b2 = c2 – теорема Пифагора для п/у треугольника К

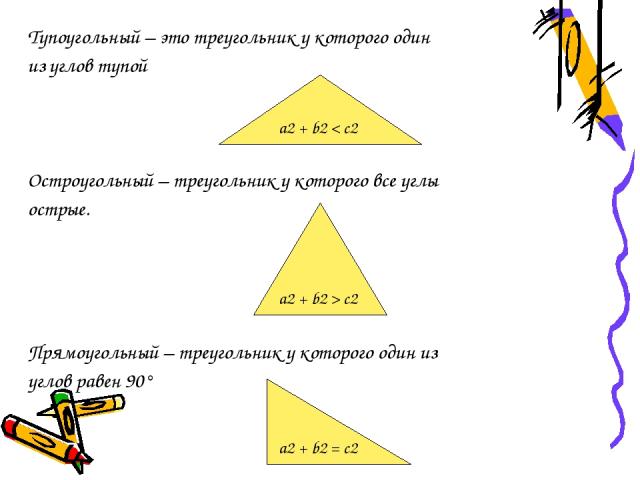
Тупоугольный – это треугольник у которого один из углов тупой Остроугольный – треугольник у которого все углы острые. Прямоугольный – треугольник у которого один из углов равен 90° a2 + b2 < c2 a2 + b2 > c2 a2 + b2 = c2

Медиана Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника. Свойства медиан треугольника: Медиана разбивает треугольник на два треугольника одинаковой площади. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Свойства биссектрис треугольника: Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Свойства биссектрис треугольника: Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. b a x y

Высота Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника. Свойства высот треугольника: В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Серединный перпендикуляр Прямую, проходящую через середину отрезка Перпендикулярно к нему, называют серединным перпендикуляром к отрезку. Свойства серединных перпендикуляров треугольника: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средняя линия Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Свойство средней линии треугольника Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Сумма углов треугольника Теорема: Сумма углов треугольника равна 180°. Доказательство: Рассмотрим треугольник АВС и докажем, что А + В + С = 180°. Проведем через вершину B прямую а, параллельную стороне АС. Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому 4 = 1, 5 = 3. Очевидно, сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е. 4 + 2 + 5 = 180°, или А + В + С = 180°. Теорема доказана. а

Внешний угол Доказательство: угол 4 – внешний угол, смежный с углом 3 данного треугольника. Т.к. 4 + 3 = 180°, а по теореме о сумме углов треугольника ( 1 + 2) + 3 = 180°, то 4 = 1 + 2, что и требовалось доказать. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Теорема: внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним

Соотношение между сторонами и углами треугольника В треугольнике против большей стороны лежит больший угол. В треугольнике против большего угла лежит большая сторона. В прямоугольном треугольнике гипотенуза больше катета. Если два угла треугольника равны, то треугольник равнобедренный

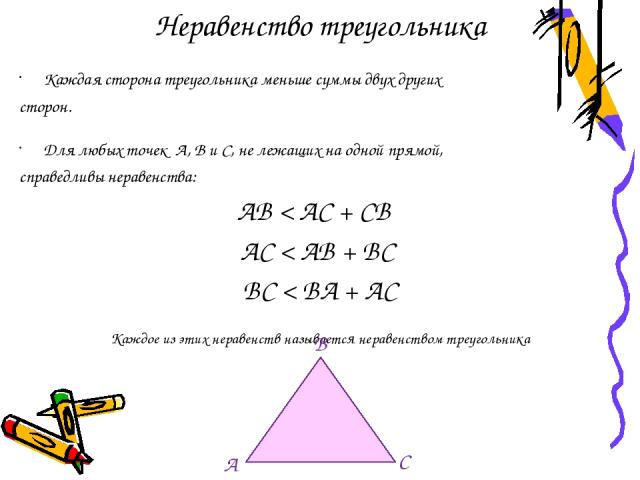
Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон. Для любых точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ < АС + СВ АС < АВ + ВС ВС < ВА + АС Каждое из этих неравенств называется неравенством треугольника B