Презентация на тему: «Подобные треугольники» 8 класс

5klass.net

1.1. Пропорциональные отрезки. 1.2. Определение подобных треугольников 1.3. Отношение площадей подобных треугольников. 1.4. Свойства подобия.

1.1 Пропорциональные отрезки. Отношением отрезков AB и CD называется отношение их длин, т. е. Говорят, что отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если ПРИМЕР №1. Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A1B1 и C1D1,отрезки которых равны 3см и 1,5см. В самом деле,

1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любые два квадрата, любые два круга. Введем понятие подобных треугольников.

1.2. Определение подобных треугольников. ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо от их размеров. Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одной и той же постоянной k, называемой коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны. Подобные фигуры F1 и F2.

1.2. Определение подобных треугольников. Задача№1. Пусть у двух треугольников ABC и A1B1C1 соответственно равны: A= A1, B= B1, C= C1. В этом случае стороны AB и A1B1, BC и B1C1, CA и C1A1 называются сходными.

1.2. Определение подобных треугольников. А B C А1 B1 C1 AB и A1B1, BC и B1C1, CA и C1A1- сходственные стороны

1.2. Определение подобных треугольников. Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A1B1C1 так, что A= A1, B= B1, C= C1, Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.

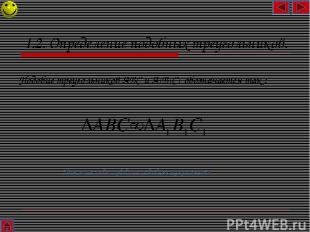
1.2. Определение подобных треугольников. Подобие треугольников ABC и A1B1C1 обозначается так : Нажмите сюда и увидите подобные треугольники

1.3. Отношение площадей подобных треугольников. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Доказательство. Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то

1.3. Отношение площадей подобных треугольников. По формулам имеем: поэтому Теорема доказана.

Свойства подобия. Задача №2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника Решение. Пусть AD – биссектриса треугольника ABC. Докажем, что Треугольники ABD и ACD имеют общую высоту AH, поэтому 1 2 A H B D C

Свойства подобия. С другой стороны, эти же треугольники имеют по равному углу( A= A1), поэтому Из двух равенств для отношений площадей получаем , или Что и требовалось доказать.

Теорема: Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. А= А1 В= В1 АВС А1В1С1

Доказательство: По теореме о сумме углов: С = 1800 - А - В, а С1 = 1800 - - А 1- В1 ,значит С= С1. Так как А= А1 и С= С1, то и От этого следует: Получается, что сходственные стороны пропорциональны. Дано: АВС и А1В1С1 А= А1 В= В1 Доказать: АВС А1В1С1 А С В А1 В1 С1

Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. АВС А1В1С1

АВС2 А1В1С1(по первому признаку) ,значит , с другой стороны ,из этих равенств получается АС= =АС2. АВС= АВС2 -по двум сторонам и углу между ними (АВ-общая сторона, АС=АС2 и ,т.к. и ).Значит и , то АВС А1В1С1 Дано: АВС и А1В1С1 Д-ть: Доказательство: Рассмотрим АВС2, у которого и

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобные. АВС А1В1С1

Доказательство: Рассмотрим АВС2, у которого и . Дано: АВС и А1В1С1 Д-ть: АВС А1В1С1 АВС2 А1В1С1(по первому признаку) ,значит и АВС= АВС2 значит , а так как , то Значит АВС А1В1С1

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Дано: АВС МN – средняя линия Доказать: МN //АС и MN=1/2AC Доказательство: ВМN и ВАС – подобны, так как В – общий BM:ВА=ВN:BC=1:2 Значит ВMN = BAC и MN/АС = 1/2 То MN//АС и MN = ½ Теорема доказана.

Меридианы треугольника пересекаются в одной точке, которая делит каждую меридиану в отношении 2:1, считая от вершины. Дано: АВС т.О – пересечение медиан ВВ1 и АА1 Доказать:

Доказательство: А1В1 – средняя линия, и А1В1//АВ, поэтому и Значит АОВ А1ОВ1(по двум углам),то Но АВ=А1В1, поэтому АО=2А1О и ВО=2В1О. Значит точка О- пересечение медиан АА1 и ВВ1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка О – пересечение медиан ВВ1 и СС1 делит каждую из них в отношении 2:1, считая от вершины. Значит точка О – пересечения медиан АА1, ВВ1и СС1 делит их в отношении 2:1, считая от вершины.

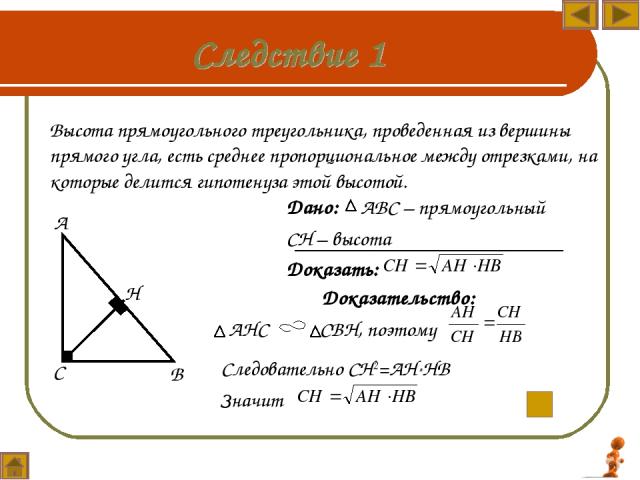
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных треугольника, каждый из которых подобен данному. Н В С А Дано: АВС – прямоугольный СН – высота Доказать: АВС АСН АВС СВН АСН СВН

Доказательство: АВС АСН(по двум углам: А- как общий и прямым), АВС ВСН(по двум углам: В- общий и прямыми), Рассмотрим АСН и ВСН – прямоугольные 1) угол АНС = углу СНВ – прямые углы 2) угол А = углу ВСН Значит АСН ВСН.

Отрезок ХY называется средним пропорциональным (или средним геометрическим) между отрезками АВ и СД, если

Дано: АВС – прямоугольный СН – высота Доказать: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. С Н А В Доказательство: АНС СВН, поэтому Следовательно СН2=АН*НВ Значит

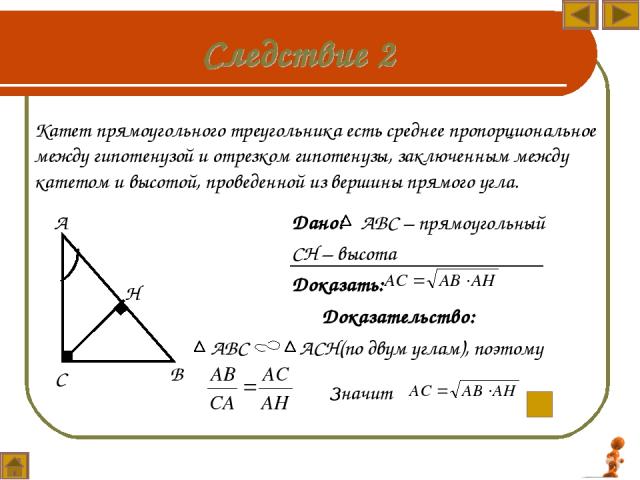
Дано: АВС – прямоугольный СН – высота Доказать: Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла. С В Н Доказательство: АВС АСН(по двум углам), поэтому Значит А

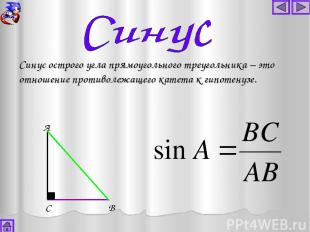
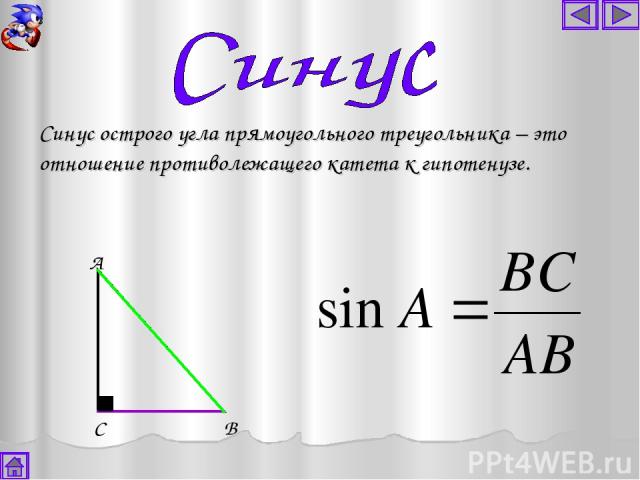
Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе. А С В

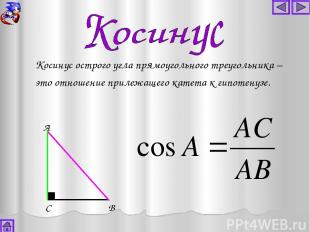
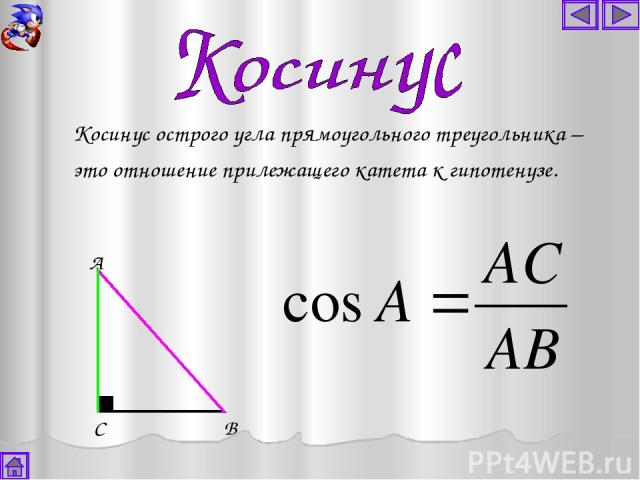
А В С Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.

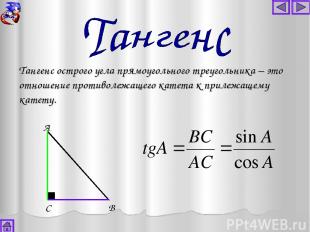
А В С Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету.

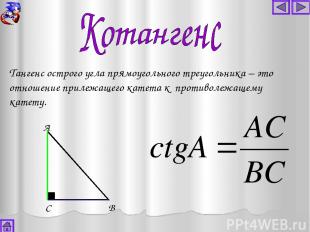
А В С Тангенс острого угла прямоугольного треугольника – это отношение прилежащего катета к противолежащему катету.

А В С

А В С АВС – прям. Т.к. в с а

А В С АВС – прям. в с а а=1 с=2 По теореме Пифагора :

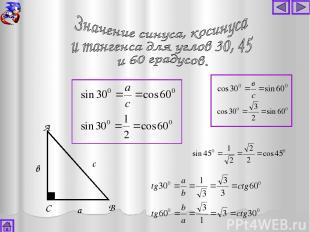
А В С в с а

А В С в с а а 300 450 600 sin a cos a tg a 1 ctg a 1