Презентация на тему: «Многогранники» стереометрия

Звездный час многогранников МКОУ «Унъюганская СОШ №2» учитель математики Ярикова Т.В. 900igr.net

Эпиграф урока: «Кто смолоду делает и думает сам, тот становится потом надёжнее, крепче, умнее.» (В. Шукшин)

Цели урока: -повторить и обобщить темы "Изображение многогранников", "Сечения многогранников"; -воспитание познавательной культуры, умение работать с дополнительной литературой, развитие памяти, интуиции, внимания, умение быстро ориентироваться в обстановке; -привитие интереса к предмету.

I тур "Домашнее задание" Творческая работа по теме «Многогранник». За самое оригинальное, полезное, соответствующее теме домашнее задание участники получают "звезду".

      Во всем облике японского строения очевидна идея преобразования пространства, подчинения его новой логике - логике "завоевания" природного ландшафта, которому противопоставлена четкая геометрия проникающих архитектурных форм     Еще один музейно-развлекательный комплекс, созданный с помощью трехмерного моделирования, продолжает тему музеев без произведений искусств.     Как объясняет создатель Музея Плодов в Яманаши Ицуко Хасегава, одна из немногих преуспевающих японских женщин-архитекторов, "геометрия трех оболочек была проанализирована с помощью объемных компьютерных построений. Каждая форма была образована путем вращения простых геометрических форм  до получения сложных  объемов.   Многогранники в архитектуре

II тур "Исправить логическую цепочку" 1. Все эти фигуры многогранники. 1) Призма; 2) тетраэдр; 3) антипризма; 4) восьмиугольник. Восьмиугольник является многоугольником

2. Соответствуют ли геометрические фигуры и их названия? 1) Призма; 2) параллелепипед; 3) пирамида; 4) куб. A. B. C. D. пирамида призма 3. Дайте название многограннику. 1) Куб; 2) призма; 3) пирамида; 4) параллелепипед. призма

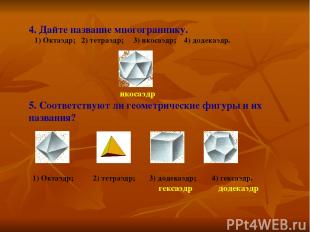
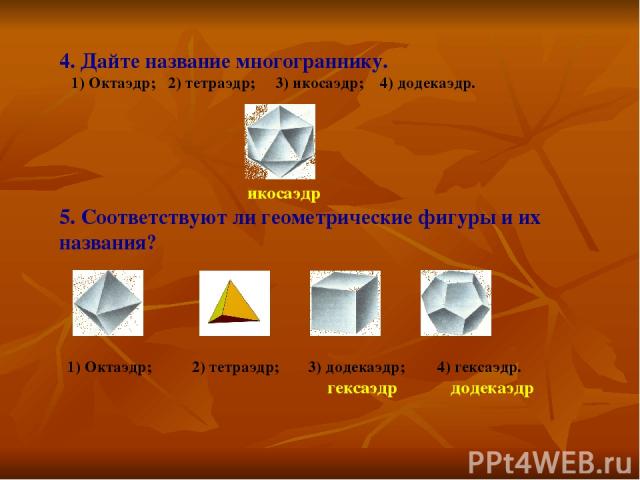
4. Дайте название многограннику. 1) Октаэдр; 2) тетраэдр; 3) икосаэдр; 4) додекаэдр. икосаэдр 5. Соответствуют ли геометрические фигуры и их названия? 1) Октаэдр; 2) тетраэдр; 3) додекаэдр; 4) гексаэдр. гексаэдр додекаэдр

Великая пирамида в Гизе. Эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности. Кроме того, это единственное из чудес, сохранившееся до наших дней. Во времена своего создания Великая пирамида была самым высоким сооружением в мире. И удерживала она этот рекорд, по всей видимости, почти 4000 лет. СТРОИТЕЛЬСТВО ПИРАМИД  Пирамиды стоят на древнем кладбище в Гизе, на противоположном от Каира, столицы современного Египта, берегу реки Нил. Некоторые археологи считают, что, возможно, на строительство Великой пирамиды 100 000 человек потребовалось 20 лет. Она была создана из более чем 2 миллионов каменных блоков, каждый из которых весил не менее 2,5 тонн. Рабочие подтаскивали их к месту, используя пандусы, блоки и рычаги, а затем подгоняли друг к другу, без раствора. ЦАРСКАЯ ГРОБНИЦА  Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.

III тур "Сечение многогранников" 1. Укажите правильное сечение:

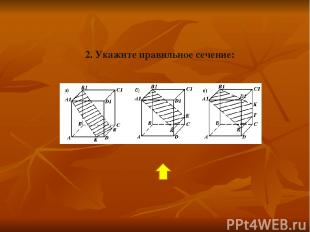
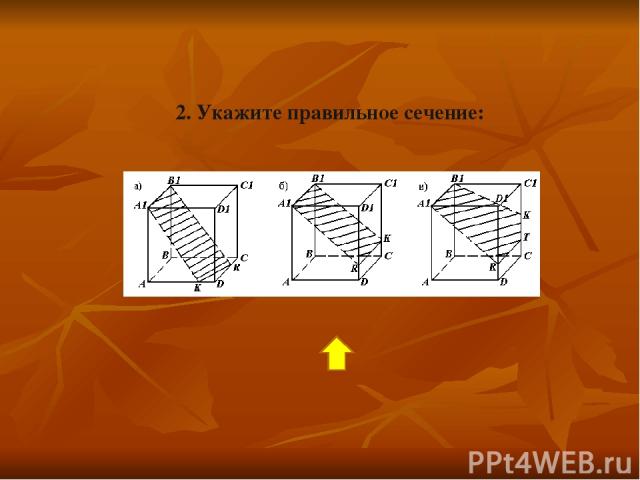
2. Укажите правильное сечение:

ПЛАТОНОВЫ ТЕЛА Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники. К каждой вершине правильного многогранника сходится одно и то же число рёбер . Все двугранные углы при рёбрах и все многогранные углы при вершинах  правильного многоугольника равны. Платоновы тела - трехмерный аналог плоских правильных многоугольников.  Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.  Также существует семейство тел, родственных платоновым - это полуправильные выпуклые многогранники, или архимедовы тела. У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов.

IV тур "Решение задач" Задача. Площадь основания треугольной пирамиды равна 10 см. Чему равна площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер? S = 2,5 см²

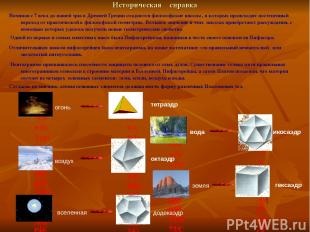
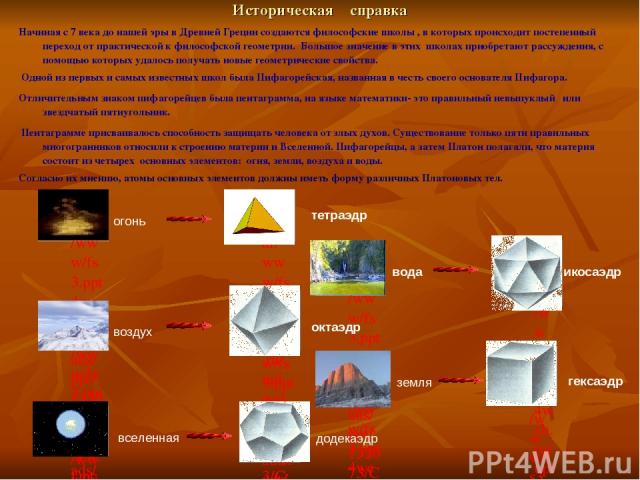
  Историческая    справка огонь вода воздух земля вселенная тетраэдр икосаэдр октаэдр гексаэдр додекаэдр Начиная с 7 века до нашей эры в Древней Греции создаются философские школы , в которых происходит постепенный переход от практической к философской геометрии.  Большое значение в этих  школах приобретают рассуждения, с  помощью которых удалось получать новые геометрические свойства.  Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый   или звездчатый пятиугольник.  Пентаграмме присваивалось способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех  основных элементов:  огня, земли, воздуха и воды. Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.

«Игра со зрителями» 1. Сколько граней у четырёхугольной пирамиды? 2. Сколько граней у пятиугольной призмы? 3. Сколько вершин имеет тетраэдр? 4. Сколько вершин имеет параллелепипед? 5. Сколько рёбер у куба? 6. Сколько граней у октаэдра? 7. Сколько граней у икосаэдра? 8. Сколько граней у додекаэдра? 5 7 4 8 12 8 20 12

V тур "Заключительный« Из слова "многогранник" составить за 1 минуту как можно больше слов.

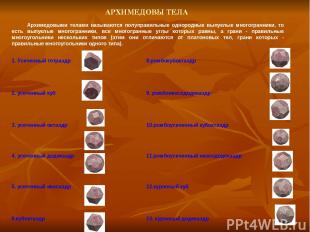
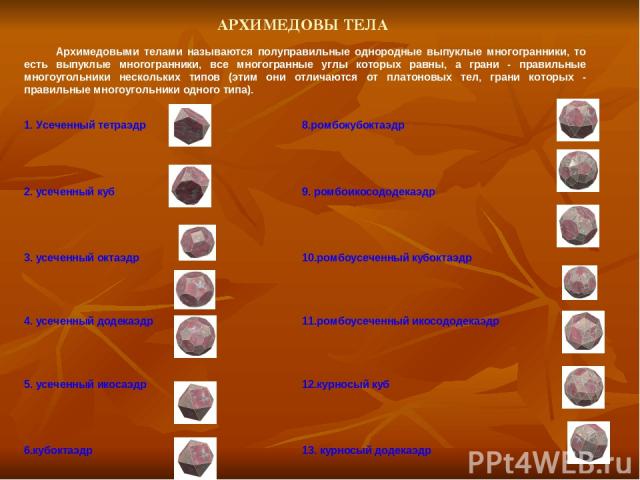
АРХИМЕДОВЫ ТЕЛА Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов (этим они отличаются от платоновых тел, грани которых - правильные многоугольники одного типа). 1. Усеченный тетраэдр            8.ромбокубоктаэдр                      2. усеченный куб                      9. ромбоикосододекаэдр            3. усеченный октаэдр                  10.ромбоусеченный кубоктаэдр                      4. усеченный додекаэдр                     11.ромбоусеченный икосододекаэдр          5. усеченный икосаэдр             12.курносый куб                       6.кубоктаэдр                       13. курносый додекаэдр            7. икосододекаэдр            14. псевдоромбокубоктаэдр                     

Подведение итогов