Презентация на тему: «Векторы» 11 класс

5klass.net

Учитель математики МОУ лицея №18 Дымова И.В

В работе рассмотрены следующие вопросы 1. История возникновения понятия вектор 2. Векторное исчисление 3. Понятие вектора 4. Коллинеарные векторы 5. Равенство векторов 6.Противоположные векторы 7.Откладывание вектора от данной точки

8.Сумма двух векторов 9.Законы сложения. 10.Правило треугольника. 11. Правило параллелограмма 12. Сумма нескольких векторов 13. Вычитание векторов 14. Умножение вектора на число

15. Компланарные векторы 16. Признак компланарности трех векторов 17. Правило параллелепипеда

История возникновения понятия вектор Понятие вектор возникло в связи с изучением величин, характеризуемых численным значением и направленностью (например, перемещение, скорость и ускорение движущейся материальной точки, действующая на неё сила и т.п.). В механике и физике рассматривают свободные, скользящие и связанные вектора.

Вектор называется свободным, если его значение не меняется при произвольном параллельном переносе. Свободным вектором является, например, скорость движения материальной точки. Вектор называется скользящим, если его значение не меняется при любом параллельном переносе вдоль линии его действия.

Примером скользящего вектора может служить сила, действующая на абсолютно твёрдое тело (две равные и расположенные на одной прямой силы оказывают на абсолютно твёрдое тело одинаковое воздействие). Вектор называется связанным, если фиксировано его начало.  

Например, сила, приложенная к некоторой точке упругого тела, представляет собой связанный вектор. Свойства свободных векторов изучаются средствами векторной алгебры (Векторное исчисление). Общее понятие вектора, как элемента, так называемого, векторного пространства определяется аксиоматически.

Векторное исчисление- математическая дисциплина, в которой изучают свойства операций над векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость).  

Возникновение и развитие векторного исчисления. Возникновение векторного исчисления тесно связано с потребностями механики и физики. До 19 в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами. Лишь в середине 19 в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания.

Основы векторного исчисления были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грассмана по гиперкомплексным числам (1844—50). Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму.

Современный вид векторному исчислению придал американский физик Дж. Гиббс. Значительный вклад в развитие векторного исчисления внесли русские учёные. В первую очередь следует отметить работы М. В. Остроградского. Им была доказана основная теорема векторного анализа (Остроградского формула).

Исследования казанского математика А. П. Котельникова по развитию винтового исчисления имели важное значение для механики и геометрии. Эти исследования были продолжены советскими математиками ПД. Н. Зейлигером и А. Широковым. Большое влияние на развитие В. и. имела книга «Векторный анализ», написанная в 1907 русским математиком П. О. Сомовым.

Понятие вектора Пусть на тело действует сила в 8Н. Стрелка указывает направление силы, а длина отрезка соответствует числовому значению силы. 8Н

Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.

Вектор характеризуется следующими элементами: 1) начальной точкой (точкой приложения); 2) направлением; 3) длиной («модулем вектора»).

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора a  . Обозначается a  . a • • B A • • • B A a

Рассмотрим произвольный отрезок. На нем можно указать два направления. Чтобы выбрать одно из направлений, один конец отрезка назовем НАЧАЛОМ, а другой – КОНЦОМ и будем считать, что отрезок направлен от начала к концу.

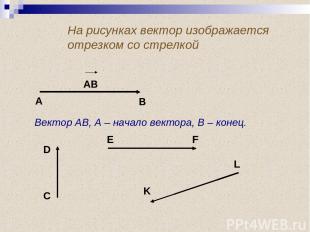
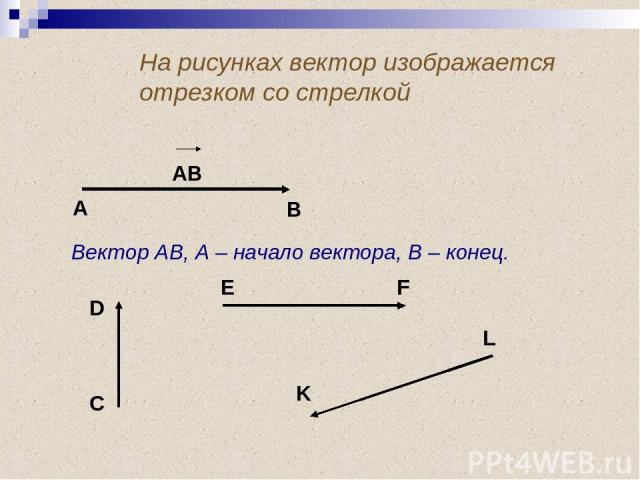
На рисунках вектор изображается отрезком со стрелкой АВ А В Вектор АВ, А – начало вектора, В – конец. D C E F K L

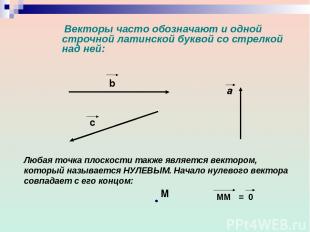
Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: b Любая точка плоскости также является вектором, который называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: c a М ММ = 0

Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ: АВ = а = АВ = 5 с a В А с = 17 Длина нулевого вектора считается равной нулю: ММ = 0. М

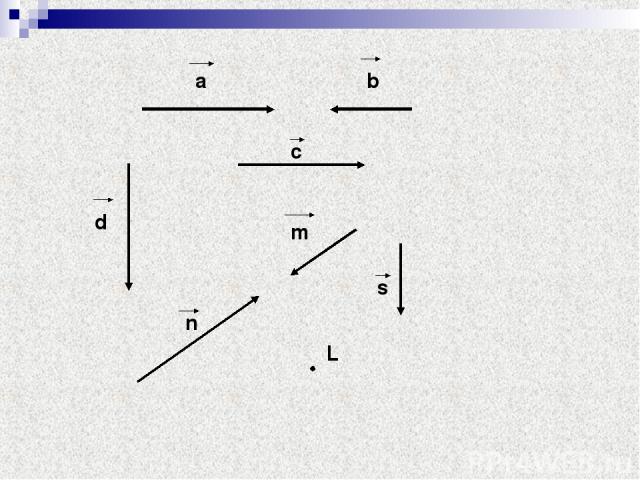
Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Допусти м, но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

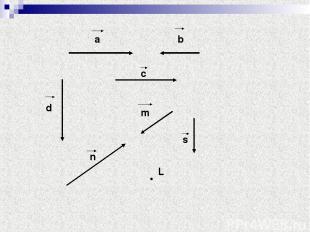
а b c d m n s L

Нулевой вектор считается коллинеарным любому вектору, так как он сонаправлен с любым вектором. a 0 a • P

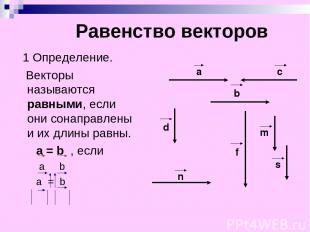
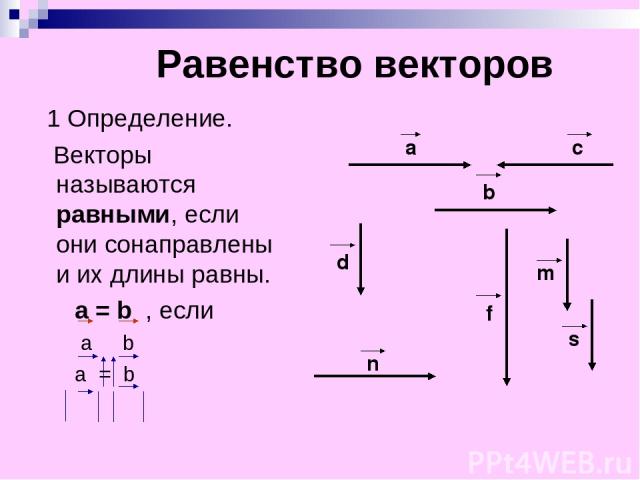
Равенство векторов 1 Определение. Векторы называются равными, если они сонаправлены и их длины равны. а = b , если а b а = b а c b d n f m s

2 Определение Два вектора называются равными, если они совмещаются параллельным переносом. АВСD — параллелограмм, AB=CD B C A D

Противоположные векторы Пусть а – произвольный ненулевой вектор. Определение. Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены. a = АВ, b = BA a B А b

Вектор, противоположный вектору c, обозначается так: -c. c - c Очевидно, с+(-с)=0 или АВ+ВА=0

Откладывание вектора от данной точки Если точка А – начало вектора а , то говорят, что вектор а отложен от точки А. Утверждение: От любой точки М можно отложить вектор, равный данному вектору а, и притом только один. Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой а А М а

Сумма двух векторов Законы сложения векторов       I.   a + b  = b + a  ( П е р е м е с т и т е л ь н ы й  закон ).     II.   ( a + b ) + c = a + ( b + c )  ( С о ч е т а т е л ь н ы й   закон ).     III.    a + 0 = a .     IV.    a + (– a ) = 0 .  

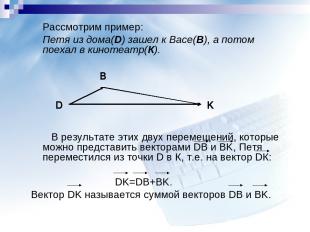
Рассмотрим пример: Петя из дома(D) зашел к Васе(B), а потом поехал в кинотеатр(К). В результате этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК: DK=DB+BK. Вектор DK называется суммой векторов DB и BK. D B K

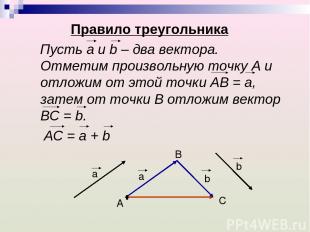
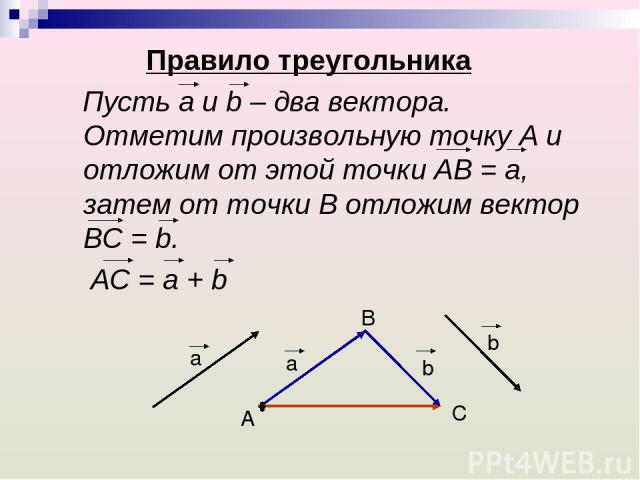
Правило треугольника Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b. АС = а + b a a b b B A C

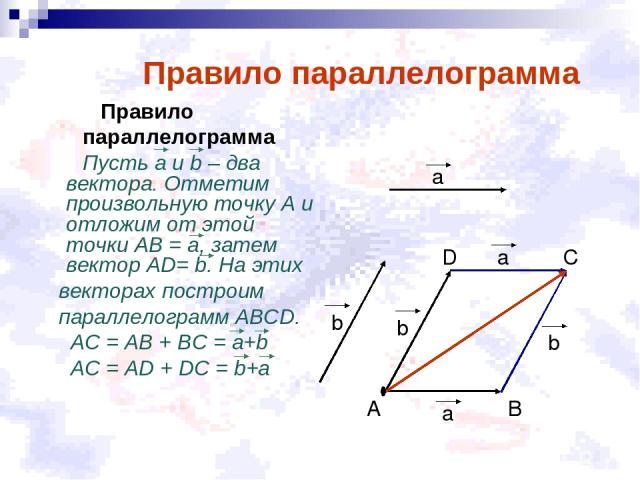
Правило параллелограмма Правило параллелограмма Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем вектор АD= b. На этих векторах построим параллелограмм АВСD. АС = АВ + BС = а+b АС = АD + DС = b+a a a a b b b D C A B

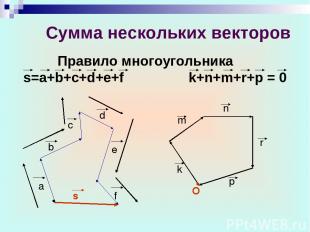
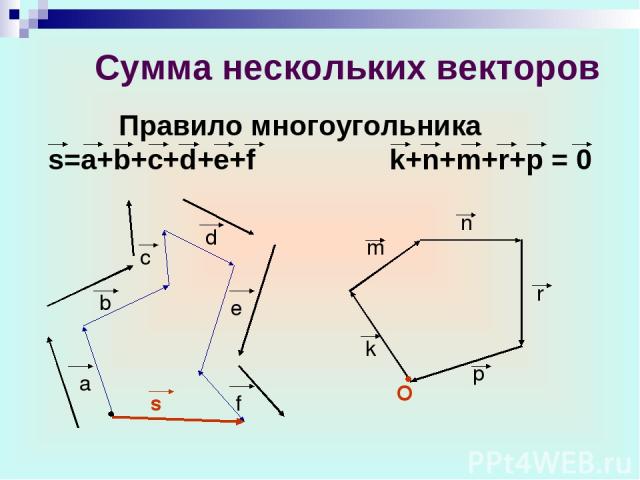
Сумма нескольких векторов Правило многоугольника s=a+b+c+d+e+f k+n+m+r+p = 0 d c e f s a b O k m n r p

Вычитание векторов Определение. Разностью двух векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а. Теорема. Для любых векторов а и b справедливо равенство а - b = а + (-b). Задача. Даны векторы а и b. Построить вектор а – b. а b -b -b а a - b

Умножение вектора на число Определение. Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна вектору k а , причем векторы а и b сонаправлены при k ≥ 0 и противоположно направлены при k < 0. а 3а -2a

Произведением нулевого вектора на любое число считается нулевой вектор. Для любого числа k и любого вектора а векторы а и ka коллинеарны. Из этого определения следует также, произведение любого вектора на число нуль есть нулевой вектор.

Умножение вектора на число Для любых чисел k, n и любых векторов а, b справедливы равенства: 1. (kn) а = k ( na ) (сочетательный закон) 2. (k + n) а = kа + na (первый распределительный закон) 3. k ( а + b ) = kа + kb (второй распределительный закон)

Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, p = 2( a – b) + ( c + a ) – 3( b – c + a ) = = 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c

Компланарные векторы [от лат. com (cum) — совместно и planum — плоскость], векторы, параллельные одной плоскости. Определение  Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости. Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.

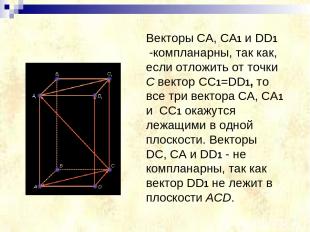
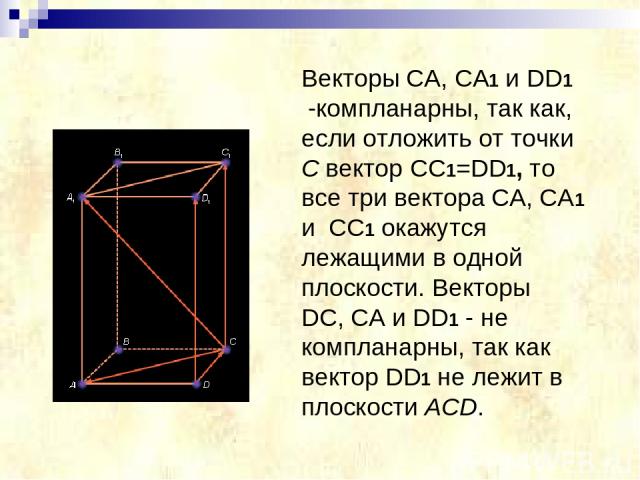
Векторы CA, CA1 и DD1  -компланарны, так как, если отложить от точки C вектор CC1=DD1, то все три вектора CA, CA1 и CC1 окажутся лежащими в одной плоскости. Векторы DC, CA и DD1 - не компланарны, так как вектор DD1 не лежит в плоскости ACD.

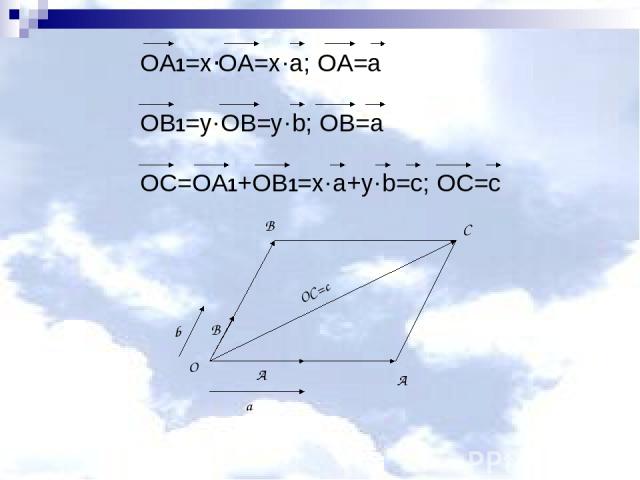
Признак компланарности трех векторов Если вектор с можно разложить по векторам a и b , т.е. представить в виде c = x·a + y·b, где где х и у — некоторые числа, то векторы a , b и c компланарны.

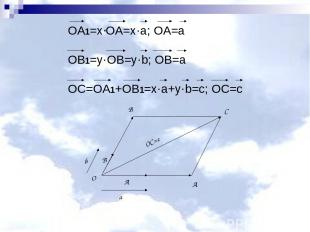
OC=c O B A b a B A C OA1=x·OA=x·a; OA=a OB1=y·OB=y·b; OB=a OC=OA1+OB1=x·a+y·b=c; OC=c

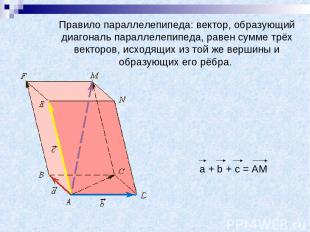
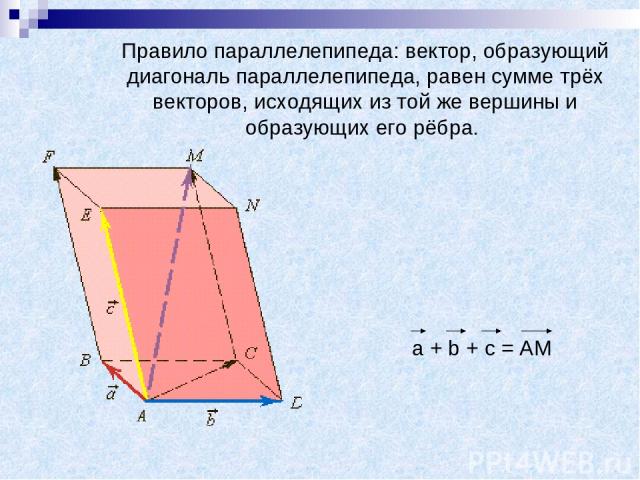
Правило параллелепипеда: вектор, образующий диагональ параллелепипеда, равен сумме трёх векторов, исходящих из той же вершины и образующих его рёбра.                                                   a + b + c = AM

Угол между двумя векторами Углом между двумя направлениями в пространстве называется величина наименьшего угла между любыми лучами этих направлений с общим началом. Угол между лучами l1 и l2 обозначается (l1 ; l2). По определению угол между двумя направлениями находится в промежутке [0°; 180°]. ^

Угол между двумя ненулевыми векторами называется угол между направлениями этих векторов. (a ; b) ^ ) a b a b

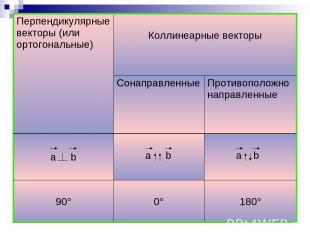
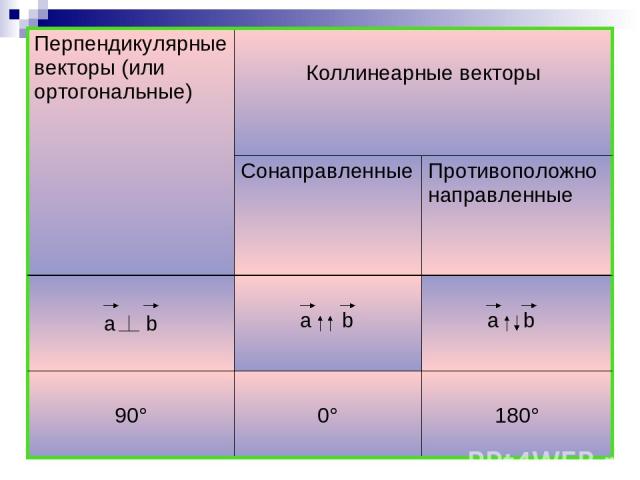
Перпендикулярные векторы (или ортогональные) Коллинеарные векторы Сонаправленные Противоположно направленные a b a b a b 90° 0° 180°