Презентация на тему: Симметрия фигур

Выполнил:Пантюков Е. А.

Оглавление Общее представление о преобразовании фигур. Общее представление о симметрии фигур Виды симметрии Симметрия относительно точки Симметрия относительно прямой

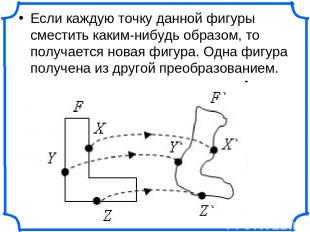
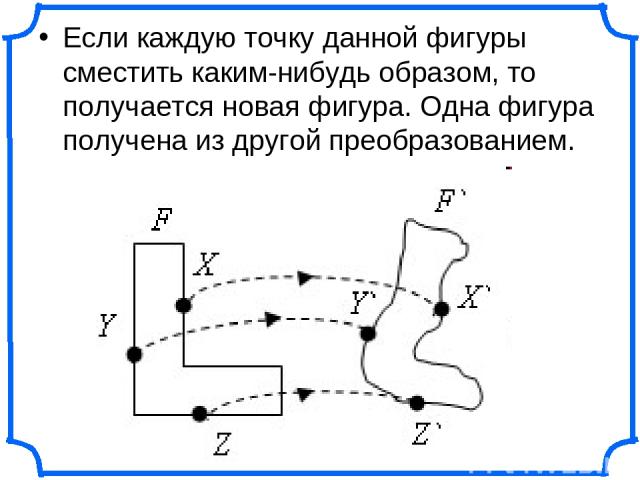
Если каждую точку данной фигуры сместить каким-нибудь образом, то получается новая фигура. Одна фигура получена из другой преобразованием.

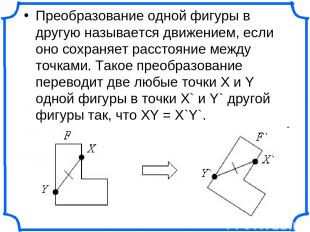
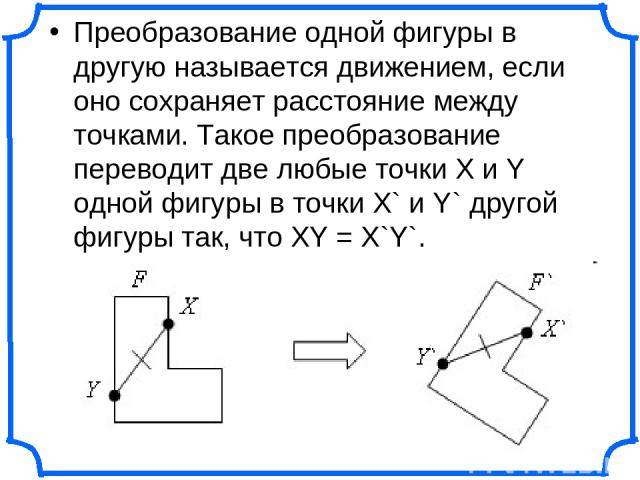
Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояние между точками. Такое преобразование переводит две любые точки X и Y одной фигуры в точки X` и Y` другой фигуры так, что XY = X`Y`.

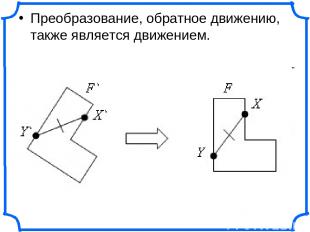
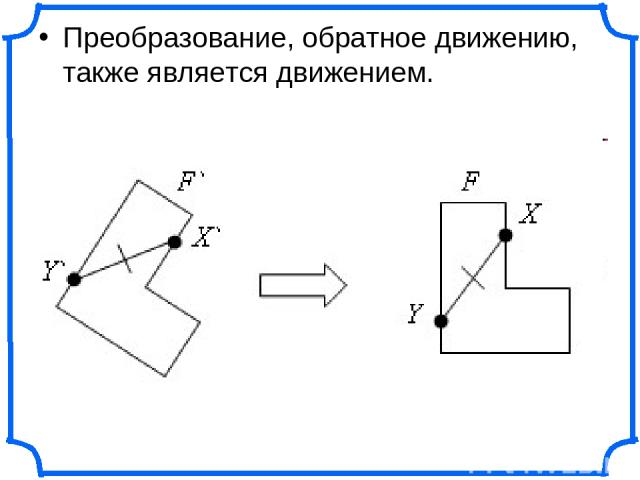
Преобразование, обратное движению, также является движением.

Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной в пространстве или на плоскости, заключающееся в закономерном повторении равных ее частей. Изучение видов симметрии имеет большое практическое и теоретическое значение для различных областей науки и техники и, особенно, при изучении строения кристаллических веществ.

Существует множество различных видов симметрии. К простейшим из них относятся: а) симметрия относительно плоскости (зеркальная симметрия); б) симметрия относительно точки (центральная симметрия); в) симметрия относительно прямой (осевая симметрия); г) симметрия вращения; д) цилиндрическая симметрия; е) сферическая симметрия.

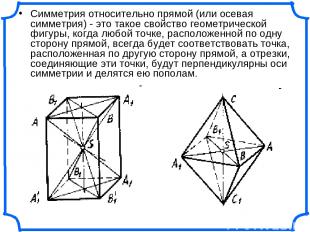
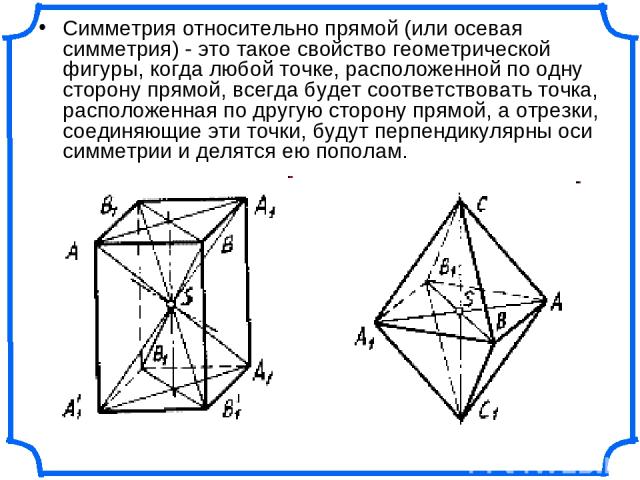
Симметрия относительно прямой (или осевая симметрия) - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.

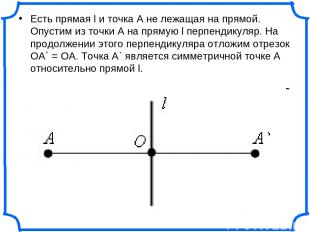
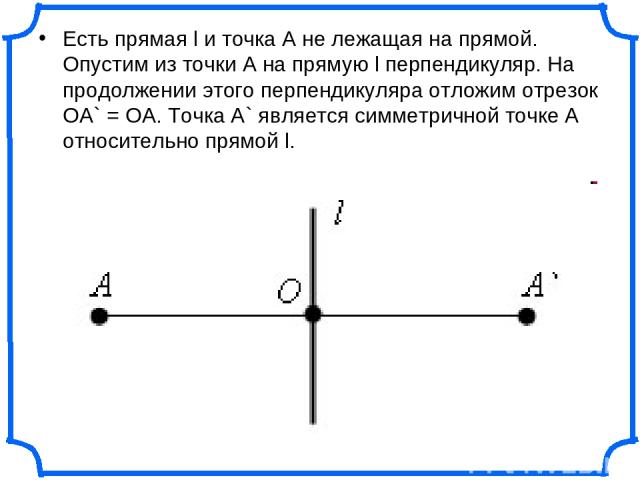
Есть прямая l и точка A не лежащая на прямой. Опустим из точки A на прямую l перпендикуляр. На продолжении этого перпендикуляра отложим отрезок OA` = OA. Точка A` является симметричной точке A относительно прямой l.

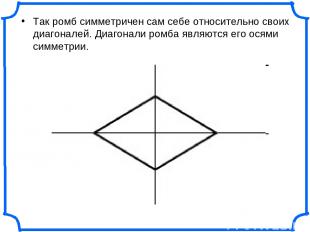
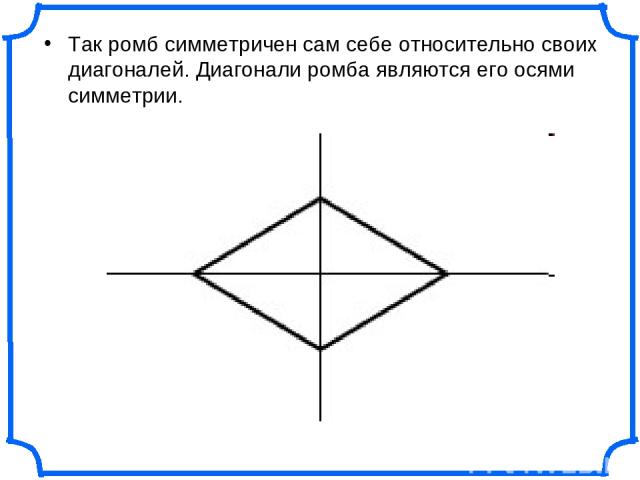
Так ромб симметричен сам себе относительно своих диагоналей. Диагонали ромба являются его осями симметрии.

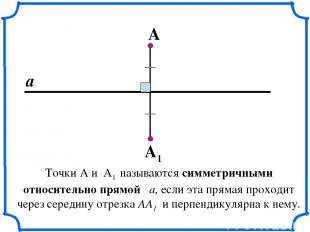
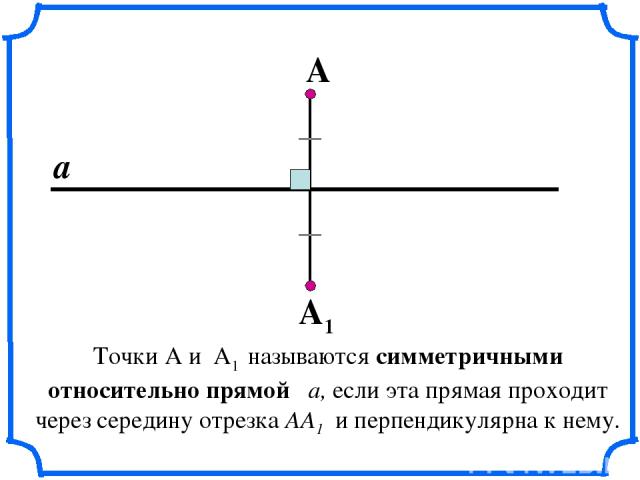
Точки А и А1 называются симметричными относительно прямой  a, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. А А1 а

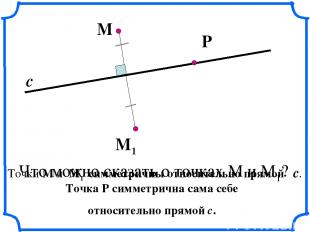
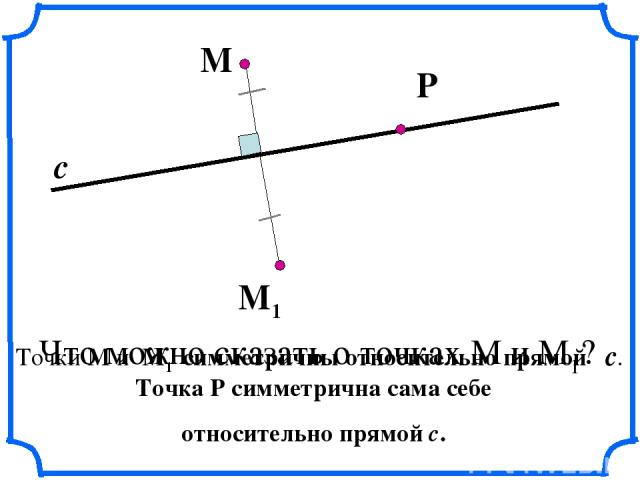
Точки М и М1 симметричны относительно прямой  с. М М1 с Что можно сказать о точках М и М1? Точка Р симметрична сама себе относительно прямой с. Р

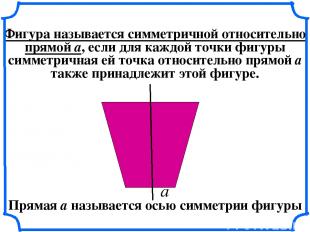
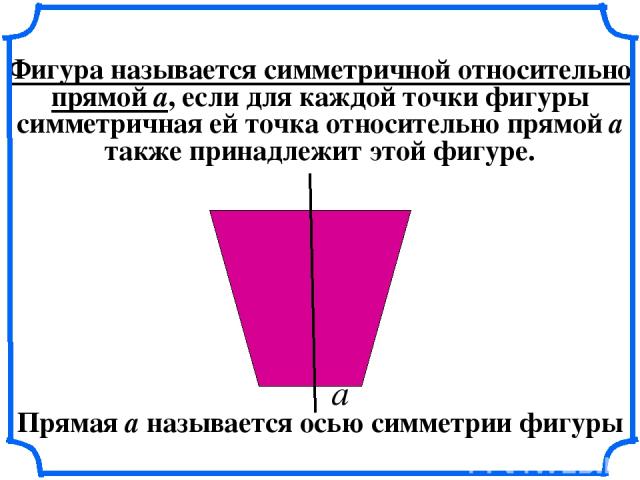
Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. а Прямая а называется осью симметрии фигуры

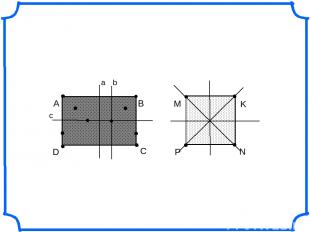
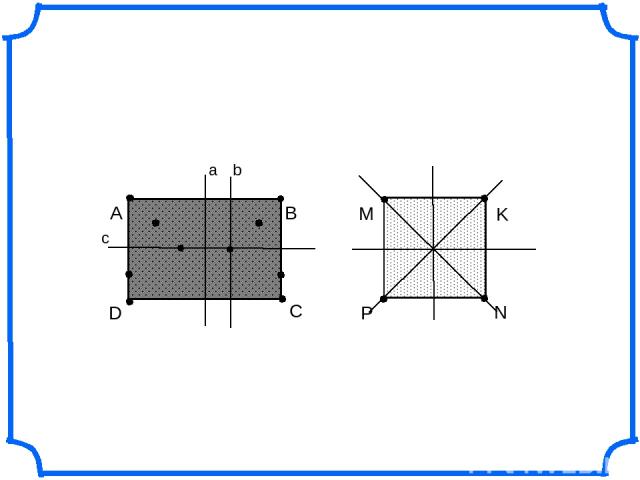
А D B C M K N P a b c

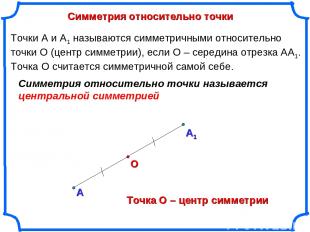
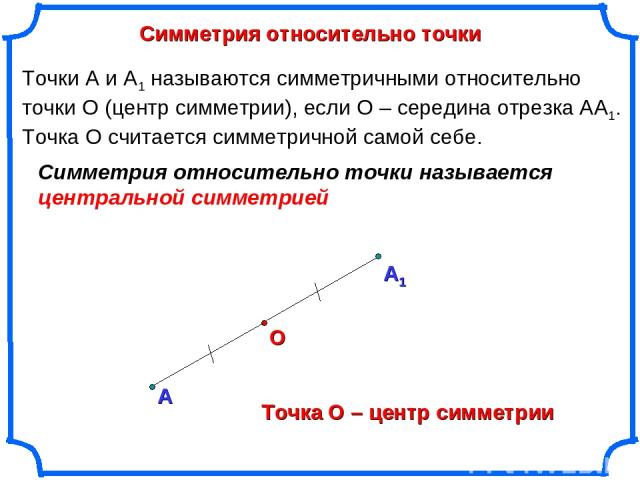
Симметрия относительно точки А О Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе. Точка О – центр симметрии Симметрия относительно точки называется центральной симметрией

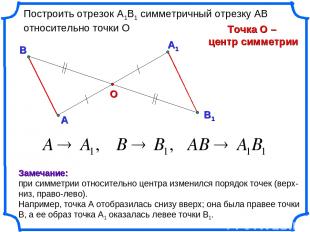
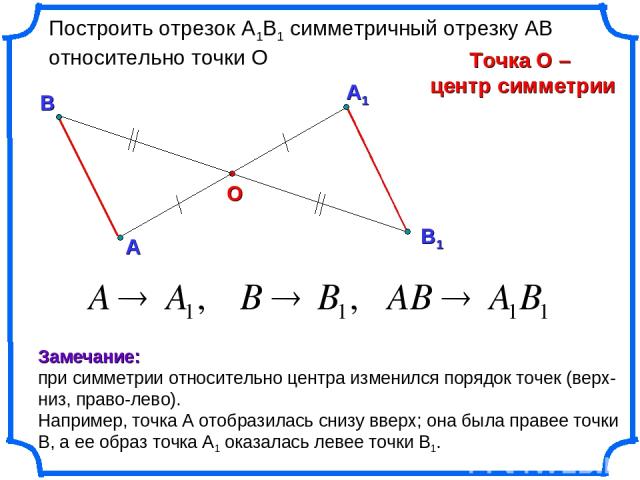
А1 А О Построить отрезок А1В1 симметричный отрезку АВ относительно точки О Точка О – центр симметрии В Замечание: при симметрии относительно центра изменился порядок точек (верх-низ, право-лево). Например, точка А отобразилась снизу вверх; она была правее точки В, а ее образ точка А1 оказалась левее точки В1.

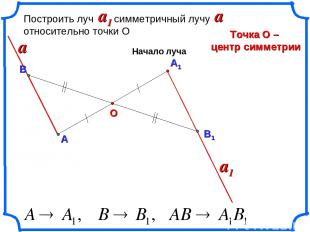
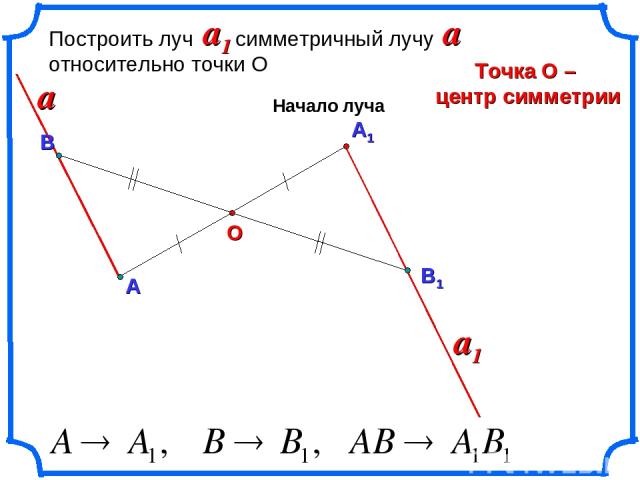
А1 О Построить луч симметричный лучу относительно точки О Точка О – центр симметрии a1 a a a1 Начало луча

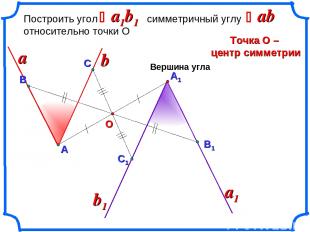
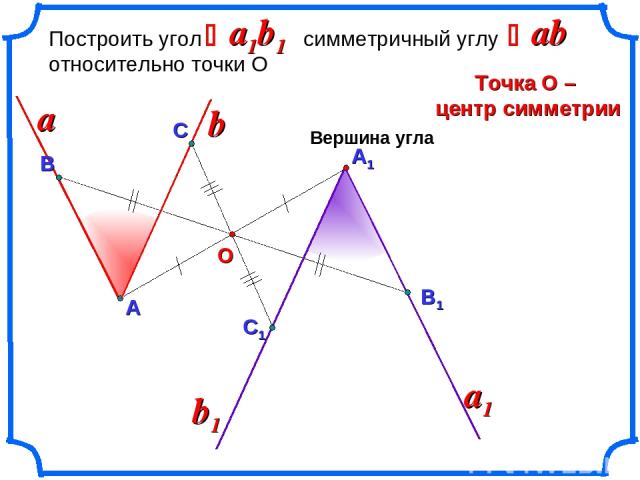
А1 Построить угол симметричный углу относительно точки О Точка О – центр симметрии a1b1 a a1 Вершина угла ab Ð Ð b О

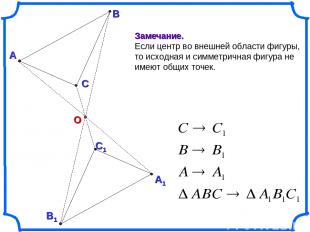
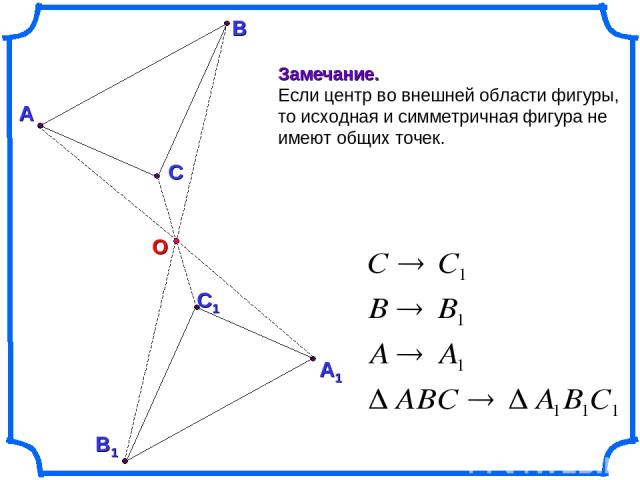
О А В В1 С С1 А1 Замечание. Если центр во внешней области фигуры, то исходная и симметричная фигура не имеют общих точек.

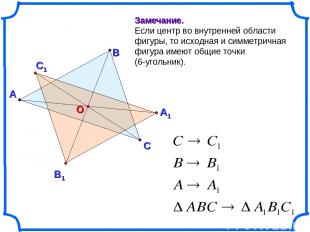
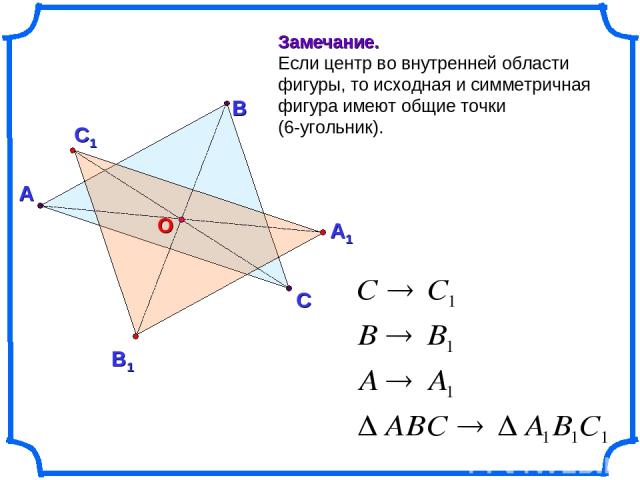
А В С Замечание. Если центр во внутренней области фигуры, то исходная и симметричная фигура имеют общие точки (6-угольник).

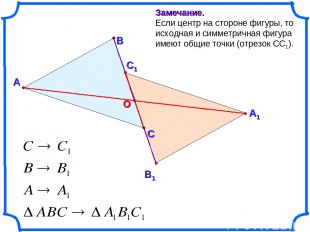
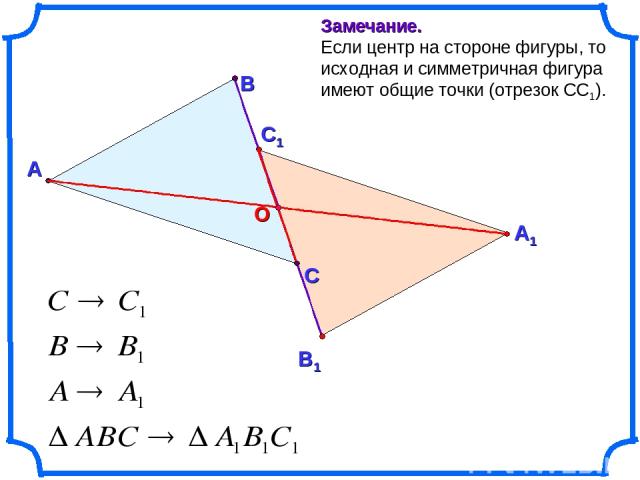
А В С Замечание. Если центр на стороне фигуры, то исходная и симметричная фигура имеют общие точки (отрезок СС1).

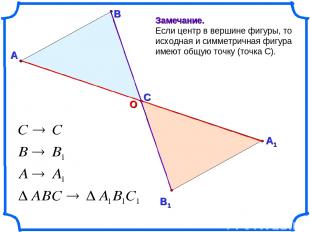
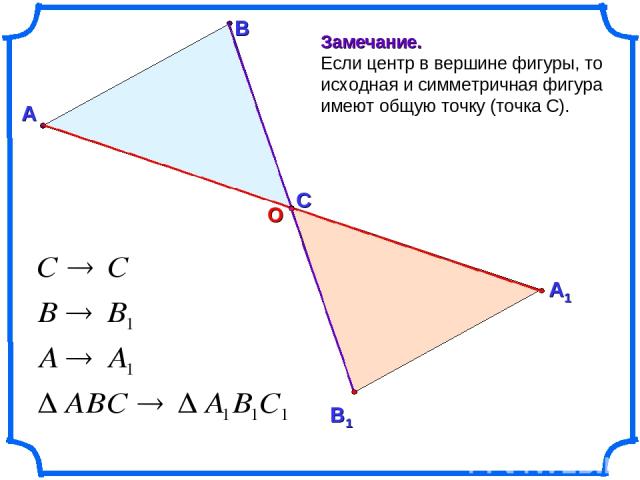
А В Замечание. Если центр в вершине фигуры, то исходная и симметричная фигура имеют общую точку (точка С). С

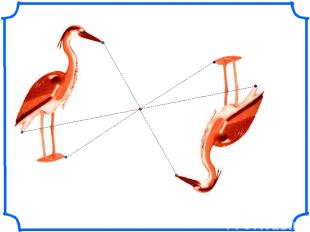
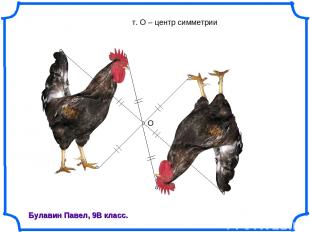
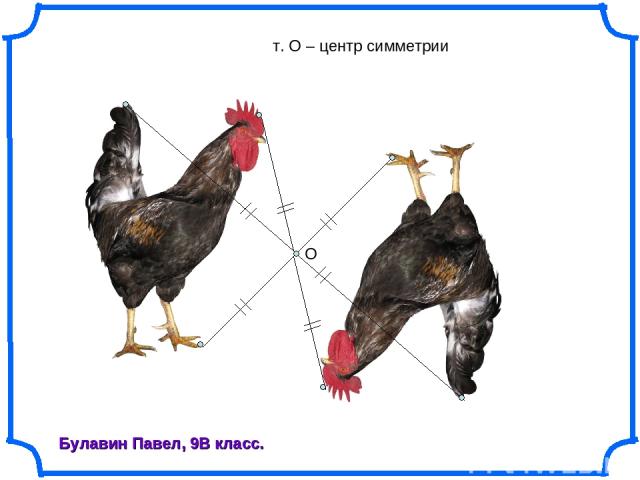
О Булавин Павел, 9В класс. т. О – центр симметрии

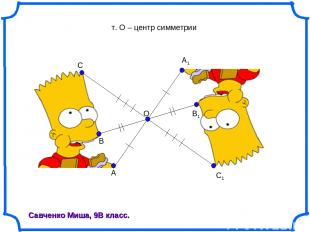
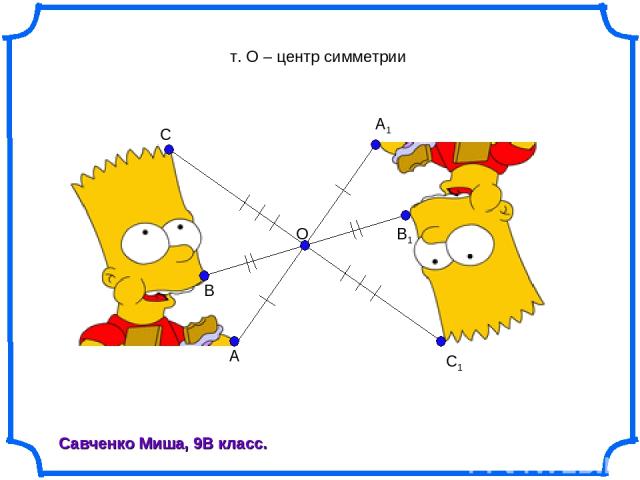
O A C1 A1 B B1 C Савченко Миша, 9В класс. т. О – центр симметрии

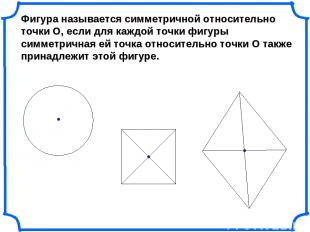
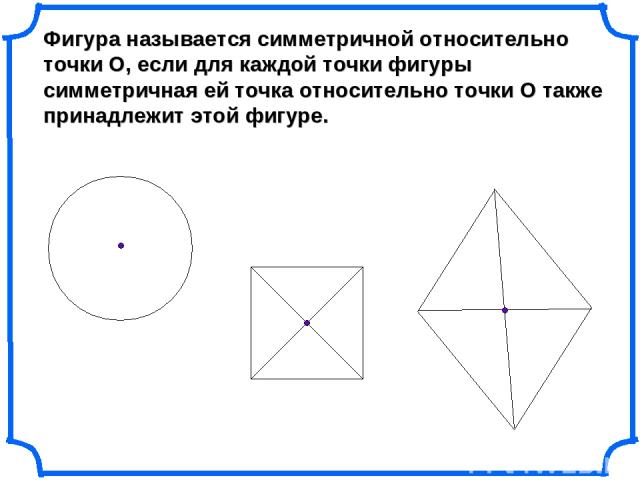
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

http://www.point.ru/photo/galleries/12876/