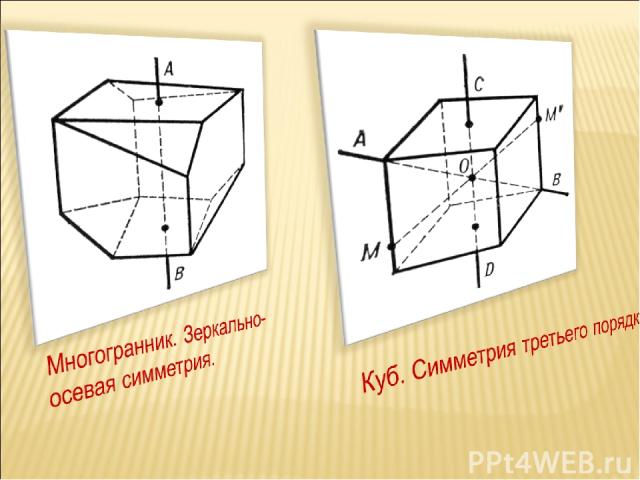
Презентация на тему: Симметрия и симметричные фигуры

Выполнили: ученики 11кл. Дюгаев Дмитрий, Сундукова Валентина Руководитель: учитель по геометрии Е. Г. Сысоева 900igr.net

Центральная симметрия; Осевая симметрия; Зеркальная симметрия; Поворотная симметрия; Симметрия в природе и геометрии; Зеркальная симметрия в природе; Список используемой литературы.

  Две точки А и А1 называются симметричными относительно точки О, если О - середина отрезка АА1. Точка О считается симметричной самой себе. На рисунке точки М и М1,  N и N1  симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки. Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О.

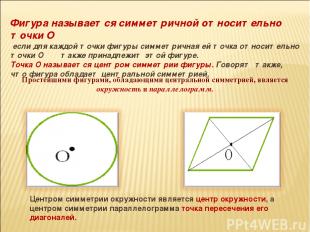
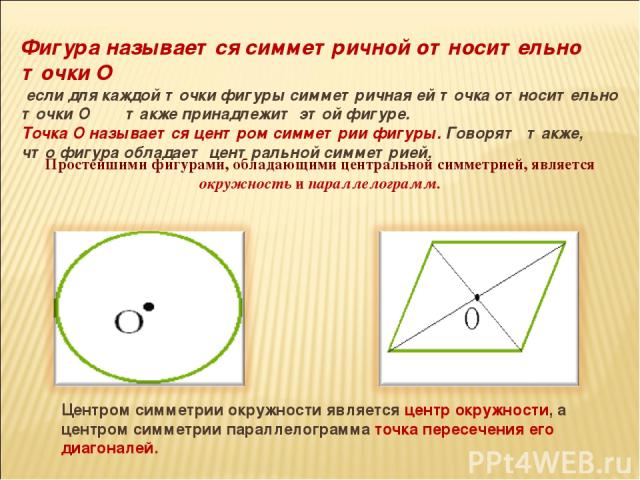
Фигура называется симметричной относительно точки О если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей.

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.    Осевая симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.

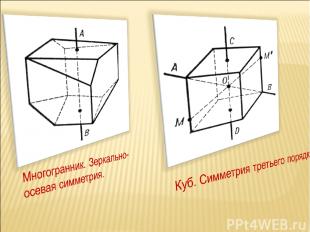
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией. У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла. Равнобедренный(но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник - три основные симметрии.

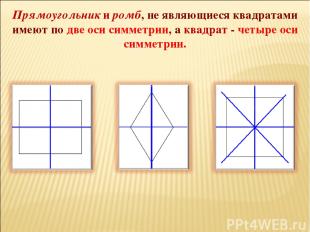
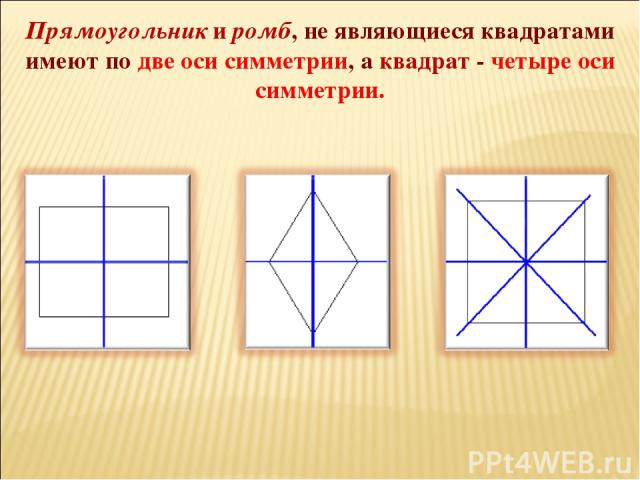
Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а квадрат - четыре оси симметрии.

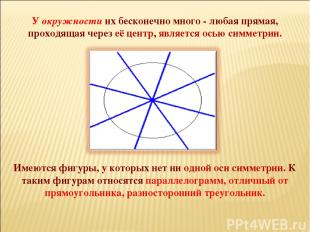
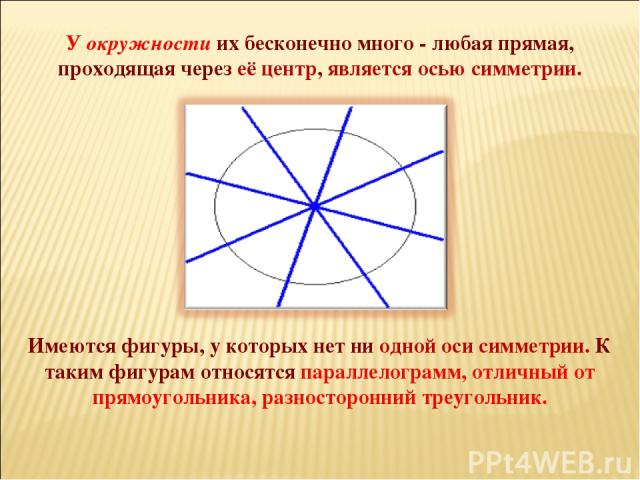
  Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник. У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.

Что может быть больше похоже на мою руку или мое ухо , чем их собственное отражение в зеркале ? И все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки.                 Иммануил Кант . Зеркальная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.

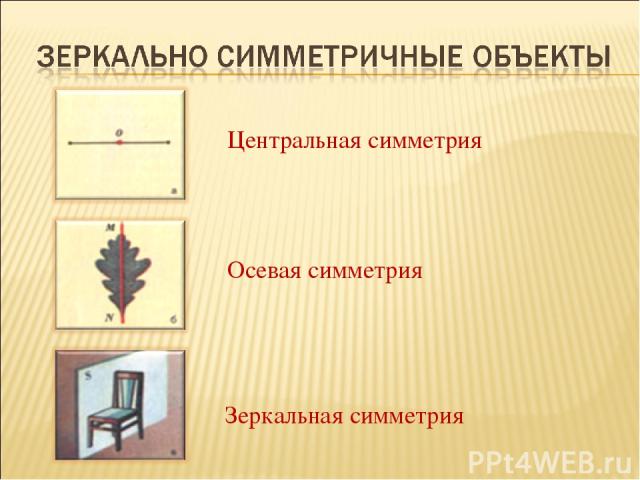
Осевая симметрия Зеркальная симметрия Центральная симметрия

Напишем на листе бумаги заглавными печатными буквами два слова "КОФЕ" и "ЧАЙ" . Затем возьмем зеркало и поставим его вертикально так , чтобы линия пересечения плоскости зеркала с плоскостью листа делила эти слова по горизонтали .

Зеркало не подействовало на слово " КОФЕ " , тогда как слово " ЧАЙ " оно изменило до неузнаваемости . Этот " фокус " имеет простое обьяснение . Разумеется , зеркало одинакововым образом отражает нижнюю половину обеих слов . Однако в отличии от слова " ЧАЙ " слово " КОФЕ " обладает горизонтальной осью симметрии , именно поэтому оно не искажается при отражении в зеркале .

Поворотная симметрия - это такая симметрия при которой объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n, где n = 2,3,4...

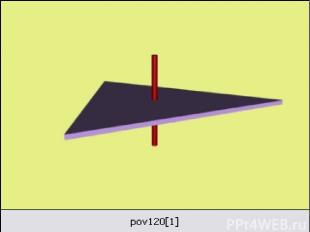
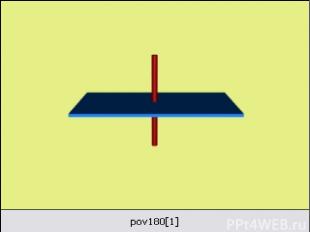
Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. С симметрией мы часто встречаемся в искусстве. архитектуре. технике. быту. Так, фасады многих зданиё обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Симметрия переноса. Симметрия. Орнамент.

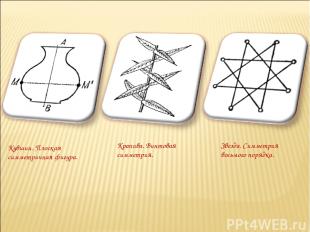
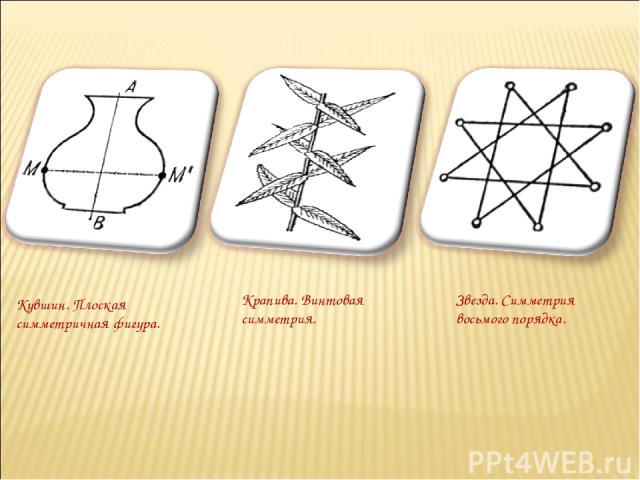
Кувшин. Плоская симметричная фигура. Крапива. Винтовая симметрия. Звезда. Симметрия восьмого порядка.

Учебник по геометрии за 11 класс Л. С. Атанасян; http://www.cisa.ru/cylinders.php; http://ru.wikipedia.org/wiki/%D0%A6%D0%B8%D0%BB%D0%B8%D0%BD%D0%B4%D1%80; http://www.college.ru/mathematics/courses/stereometry/content/chapter5/section/paragraph1/theory.html; http://www.bestreferat.ru/referat-46823.html; http://www.terver.ru.