Презентация на тему: Симметрия в окружающем мире

ГКООУ ЛO «Лужская санаторная школа-интернат» Презентация на тему «Геометрия в цветах» Подготовила ученица 10 класса Ильина любовь Проверил учитель: Мехнина С.В.. 5klass.net

План 1. Симметрия в математике 2. Симметрия в живой природе 3. Скалярная геометрия «Цветок Жизни» 4. Симметрия у цветков и растений 5. Радиальная симметрия 6. Симметрия в химии 7.Симметрия вокруг нас

СИММЕТРИЯ В МАТЕМАТИКЕ Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии.

   Древние греки полагали, что Вселенная симметрична просто потому, что симметрия прекрасна. Исходя из соображений симметрии, они высказали ряд догадок.

Пифагор (5 век до н.э.), считает сферу наиболее симметричной и совершенной формой, делал вывод о сферичности Земли и о ее движении по сфере. При этом он полагал, что Земля движется по сфере некоего «центрального огня». Вокруг того же «огня», согласно Пифагору, должны были обращаться известные в те времена шесть планет, а также Луна, Солнце, звезды

Симметрия в живой природе Прежде всего познакомимся с основными понятиями теории симметрии. Такие, которые совершенно одинаковы, или, точнее, которые при взаимном наложении совмещаются друг с другом во всех своих деталях, как, например, два лепестка на рисунке 1. Пары лепестков: а — совместимо равные; б — зеркально равные; в — и совместимо и зеркально равные. Фигуры из пяти лепестков: г — расположенных относительно друг друга хаотично; д — закономерно. Верхняя фигура асимметричная, нижняя — симметричная.

Переносы — это перемещения вдоль прямой АВ на расстояние а. Такая операция применима лишь для объектов, вытянутых в одном особенном направлении АВ. Наименьший путь а, который должен быть пройден рядом фигур, прежде чем произойдет самосовмещение, называется элементарным переносом. Операции переноса также соответствует особый элемент симметрии — ось переносов (а):прямая АВ или любая прямая, параллельная АВ. Ось переносов (о) присуща только бесконечным фигурам, тем, которые бесконечно вытянуты лишь в одном особенном направлении (типа «стержней»), в двух особенных направлениях (типа «слоев»), в трех особенных направлениях (типа «кристаллов»). При этом считается, что телам, не вытянутым бесконечно ни в одном особенном направлении (типа изображенных на рисунках 2, 3, 4, 5), присуща нульмерная симметрия; телам, вытянутым в одном особенном направлении, — одномерная симметрия, в двух — двумерная симметрия, в трех — трехмерная симметрия. А теперь каждую из этих симметрии рассмотрим по порядок. Аксиальная симметрия: а — медуза аурелия инсулинда; б — детская вертушка; в — молекула химического соединения. При повороте этих фигур на 360о равные части фигур совпадут друг с другом соответственно 4, 4, 6 раз.

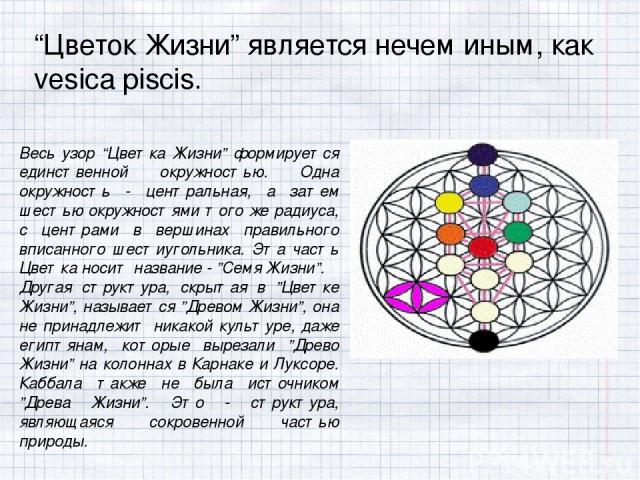
Сакральная геометрия – Цветок Жизни “Цветок Жизни” - единственное изображение, которое содержит в себе до единого аспекты творения, все математические формулы, каждый закон физики, каждую гармонию в музыке и каждую биологическую жизнеформу. Сакральная геометрия имеет одну особенность — она безупречна, всё в мире связано с ней, она основа творения, в геометрии “Цветка Жизни” заключен образ творения. Всё, что существует в мире или было когда-либо сотворено, создавалось по этому образцу и имеет в своей основе сакральную геометрию.

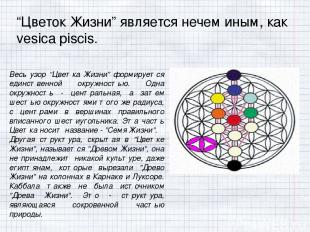
“Цветок Жизни” является нечем иным, как vesica piscis. Весь узор “Цветка Жизни” формируется единственной окружностью. Одна окружность - центральная, а затем шестью окружностями того же радиуса, с центрами в вершинах правильного вписанного шестиугольника. Эта часть Цветка носит название - ”Семя Жизни”. Другая структура, скрытая в ”Цветке Жизни”, называется ”Древом Жизни”, она не принадлежит никакой культуре, даже египтянам, которые вырезали ”Древо Жизни” на колоннах в Карнаке и Луксоре. Каббала также не была источником ”Древа Жизни”. Это - структура, являющаяся сокровенной частью природы.

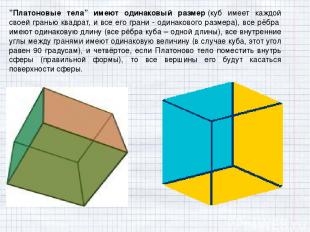
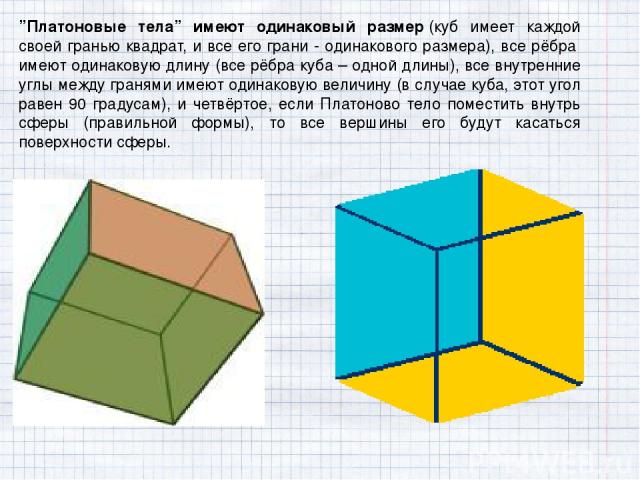
”Платоновые тела” имеют одинаковый размер (куб имеет каждой своей гранью квадрат, и все его грани - одинакового размера), все рёбра  имеют одинаковую длину (все рёбра куба – одной длины), все внутренние углы между гранями имеют одинаковую величину (в случае куба, этот угол равен 90 градусам), и четвёртое, если Платоново тело поместить внутрь сферы (правильной формы), то все вершины его будут касаться поверхности сферы. 

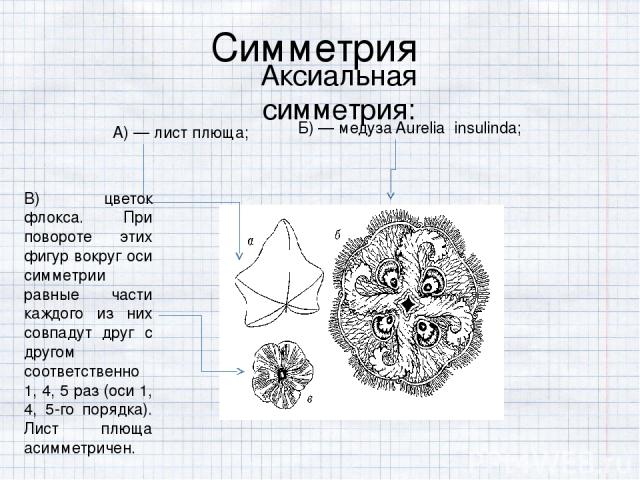
Симметрия Аксиальная симметрия:   А) — лист плюща; Б) — медуза Aurelia insulinda; В) цветок флокса. При повороте этих фигур вокруг оси симметрии равные части каждого из них совпадут друг с другом соответственно 1, 4, 5 раз (оси 1, 4, 5-го порядка). Лист плюща асимметричен.

б — лист кислицы; симметрии соответственно 1․m, 3․m. Бабочке свойственна двусторонняя, или билатеральная, симметрия. Актиноморфная симметрия  а) — бабочка

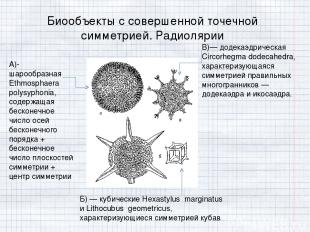
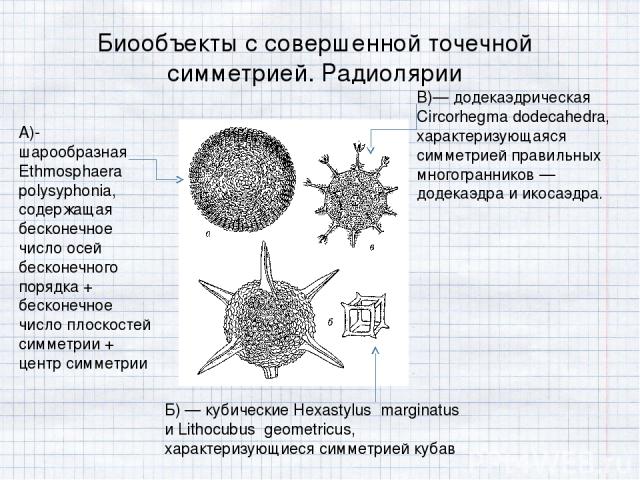
В)— додекаэдрическая Circorhegma dodecahedra, характеризующаяся симметрией правильных многогранников — додекаэдра и икосаэдра. Биообъекты с совершенной точечной симметрией. Радиолярии А)- шарообразная Ethmosphaera polysyphonia, содержащая бесконечное число осей бесконечного порядка + бесконечное число плоскостей симметрии + центр симметрии Б) — кубические Hexastylus marginatus и Lithocubus geometricus, характеризующиеся симметрией кубав

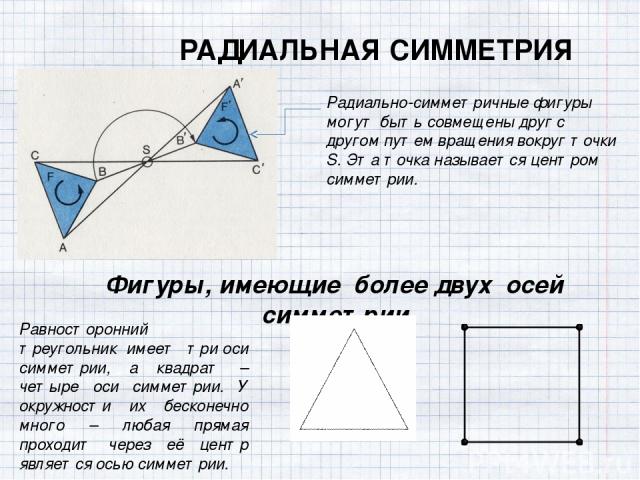
РАДИАЛЬНАЯ СИММЕТРИЯ Радиально-симметричные фигуры могут быть совмещены друг с другом путем вращения вокруг точки S. Эта точка называется центром симметрии. Фигуры, имеющие более двух осей симметрии Равносторонний треугольник имеет три оси симметрии, а квадрат – четыре оси симметрии. У окружности их бесконечно много – любая прямая проходит через её центр является осью симметрии.

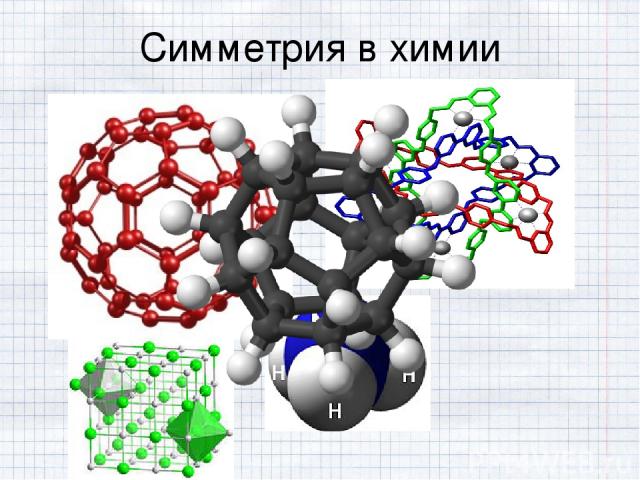
Симметрия в химии

Симметрия (в химии) Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается на специфике физических и химических свойств молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами. Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии и т. д.

Симметрия вокруг нас