Презентация на тему: Сечение многогранников

Сечения многогранников 10 класс Геометрия Петрушенко Ирина Владимировна, учитель математики МОУ «СОШ№2» г. Калачинск, Омская область 18.11.2009 5klass.net

Определения: Секущая плоскость - плоскость, по обе стороны от которой имеются точки данного многогранника. Многоугольник – сторонами которого являются отрезки пересекающие грани по секущей плоскости многогранника называется сечением данного многогранника (часть секущей плоскости, заключенная внутри тела).

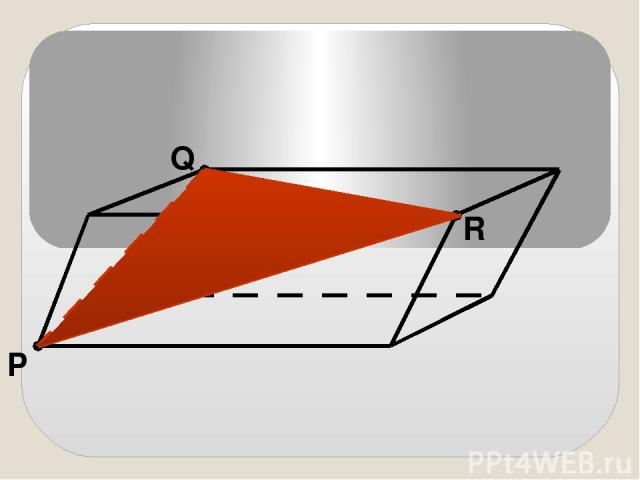
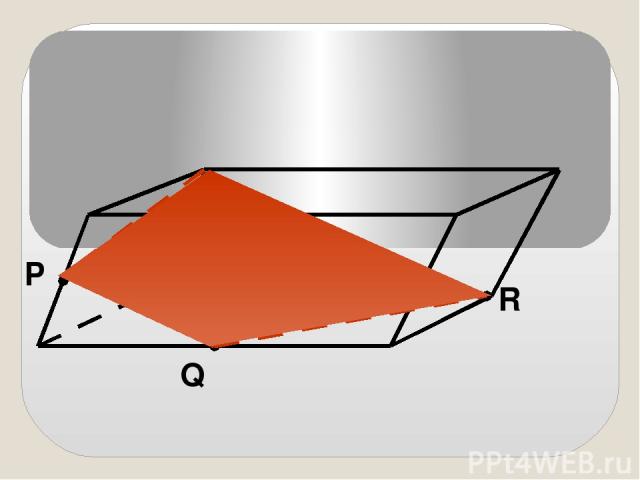
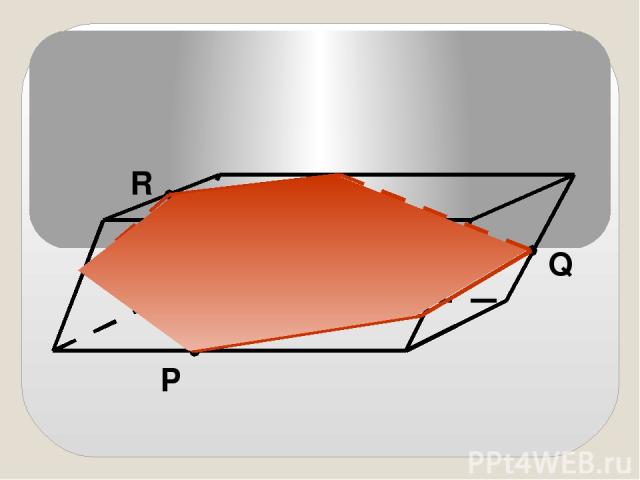
Сечениями могут быть: 3-угольники и 4-угольники (если многогранник – тетраэдр, имеющий 4 грани). 3-угольники, 4-угольники, 5-угольники и 6-угольники (если многогранник – параллелепипед, имеющий 6 граней).
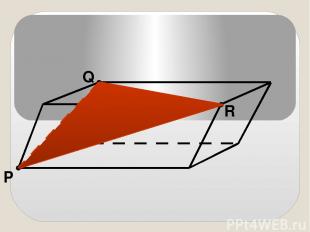
P Q R
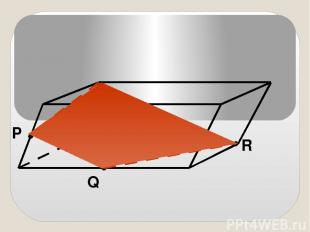
P Q R
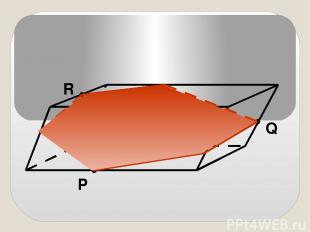
P Q R

Основные виды сечений многогранников: Параллельное сечение – сечение, плоскость которого параллельна либо основанию, либо одной из грани многогранника. Диагональное сечение – сечение, плоскость которого, проходит через диагонали многогранника, или диагонали оснований многогранника.

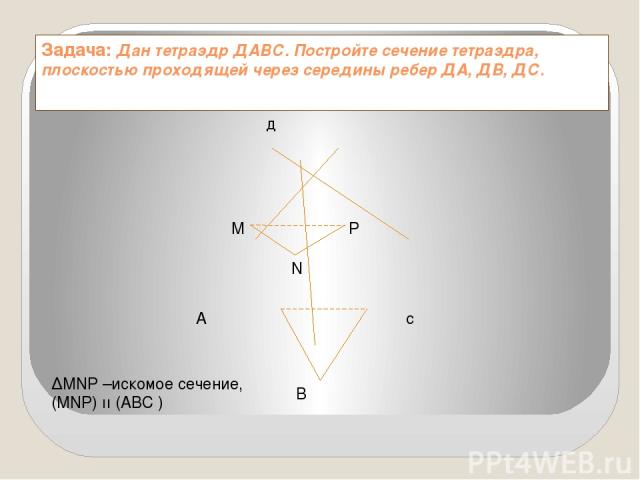
Задача: Дан тетраэдр ДАВС. Постройте сечение тетраэдра, плоскостью проходящей через середины ребер ДА, ДВ, ДС. д А с M N P B ∆MNP –искомое сечение, (MNP) ıı (ABC )

Методы построения сечений: Аксиоматический метод: метод следов; использование свойств параллельных плоскостей; метод вспомогательных сечений. Комбинированный метод.

Метод следов: Прямая, по которой секущая плоскость пересекает плоскость грани многогранника называется следом секущей плоскости в плоскости этой грани. RQ – прямая, являющаяся следом (RQP) на (ВВ´СС´)

Правила для самоконтроля: Вершины сечения находятся только на ребрах. Стороны сечения находятся только на грани многогранника. Секущая плоскость пересекает грань или плоскость грани, то только один раз.

План построения линий пересечения плоскостей: Указать общие точки. Построить недостающие точки: а) найти пары точек на одной грани; б) построить четвертую точку в плоскости; Если пункт а) и б) не работают, то нужно строить 5 точку.

Желаем успеха при решении задач на построение сечений многогранников! Разделите каждую изучаемую вами задачу на столько частей, на сколько сможете и на сколько потребуется вам, чтобы их было легко решить. Рене Декарт