Презентация на тему: Свойство биссектрисы угла треугольника

СВОЙСТВО БИССЕКТРИСЫ УГЛА ТРЕУГОЛЬНИКА Разинкова Т.Н. специализированная школа № 6 г. Свердловск Луганской области 900igr.net

З А Д А Ч А - Т Е О Р Е М А СВОЙСТВО БИССЕКТРИСЫ ТРЕУГОЛЬНИКА ДЕЛИТ ПРОТИВОЛЕЖАЩУЮ СТОРОНУ НА ОТРЕЗКИ, ПРОПОРЦИОНАЛЬНЫЕ ПРИЛЕЖАЩИМ СТОРОНАМ БИССЕКТРИСА УГЛА ТРЕУГОЛЬНИКА

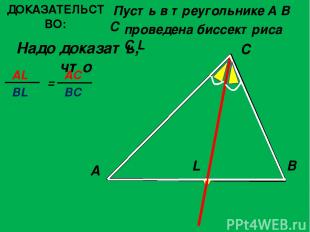
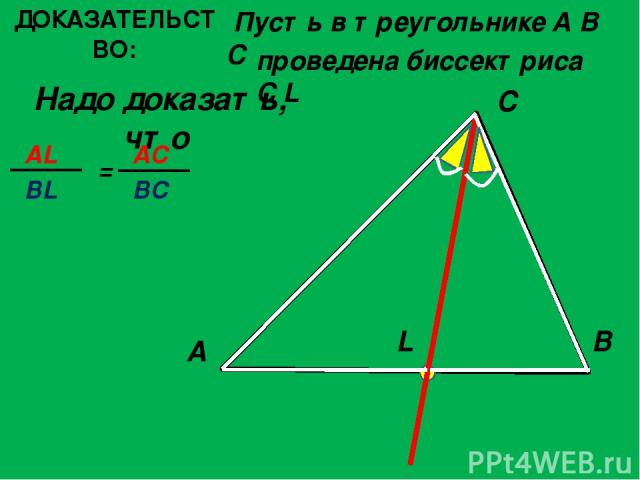
ДОКАЗАТЕЛЬСТВО: Пусть в треугольнике A B C Надо доказать, что A C B L проведена биссектриса C L AL BL = AC BC

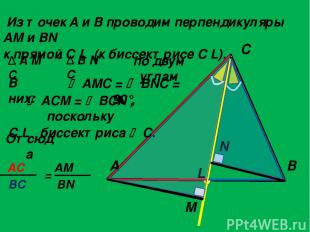
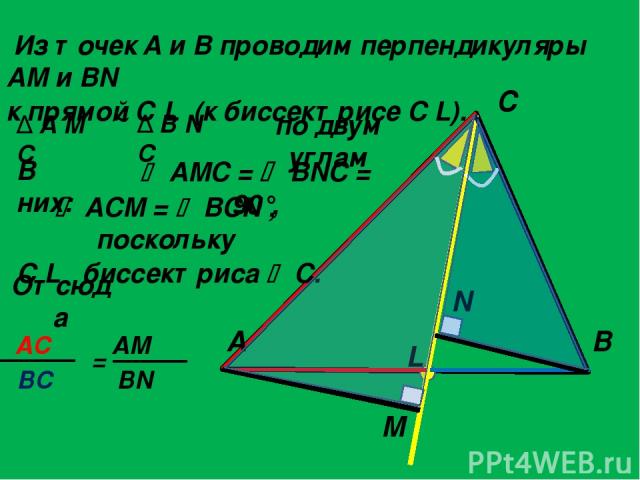
Из точек A и B проводим перпендикуляры AM и BN к прямой C L (к биссектрисе C L). по двум углам A C B L M N Δ A M C Δ B N C AMC = BNC = 90°, Отсюда ACM = BCN , поскольку C L биссектриса C. В них: AС = AM BC BN

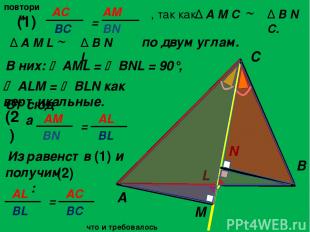
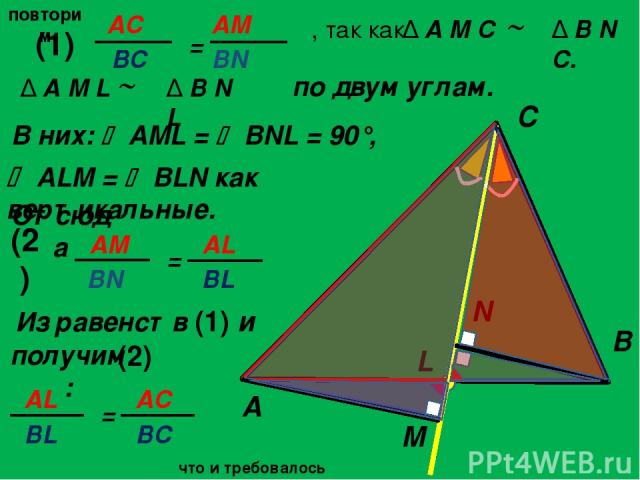
повторим по двум углам. A C B L M N , так как Δ B N C. ALM = BLN как вертикальные. Отсюда Δ A M L Δ B N L (1) (2) Из равенств (1) и (2) получим: В них: AML = BNL = 90°, Δ A M C что и требовалось доказать. AС = AM ВС BN AM = AL BN BL AL BL = AC BC