Презентация на тему: Симметрия геометрических фигур

Когда красота притягивает, а исследование увлекает Слово «симметрия» в переводе с греческого означает «одинаковость в расположении частей» Симметрия… есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. Герман Вейль Сизов Леонид Ученик 10 «б» класса МОУ «Комсомольская СОШ №1» с. Комсомольское Чувашская Республика 900igr.net

Цель исследования: Выяснить, какие геометрические фигуры имеют осевую симметрию; Определить, какая из геометрических фигур обладает наибольшим количеством симметрий Найти геометрические фигуры не обладающие симметрией

Гипотеза В планиметрии есть фигуры, обладающие осевой симметрией.

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Эта прямая называется осью симметрии.

Неразвернутый угол Неразвернутый угол имеет одну ось симметрии – прямую, на которой расположена биссектриса угла.

Равнобедренный треугольник Равнобедренный треугольник имеет одну ось симметрии.

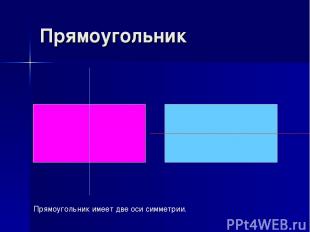
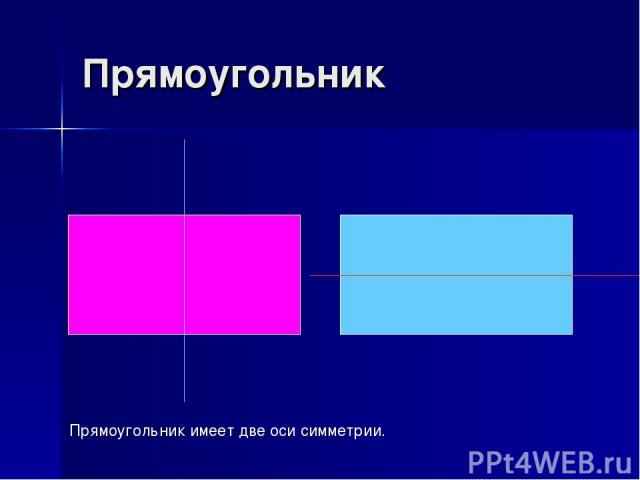
Прямоугольник Прямоугольник имеет две оси симметрии.

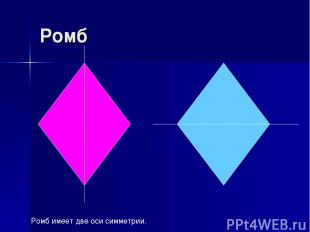
Ромб Ромб имеет две оси симметрии.

Равносторонний треугольник Равносторонний треугольник имеет три оси симметрии.

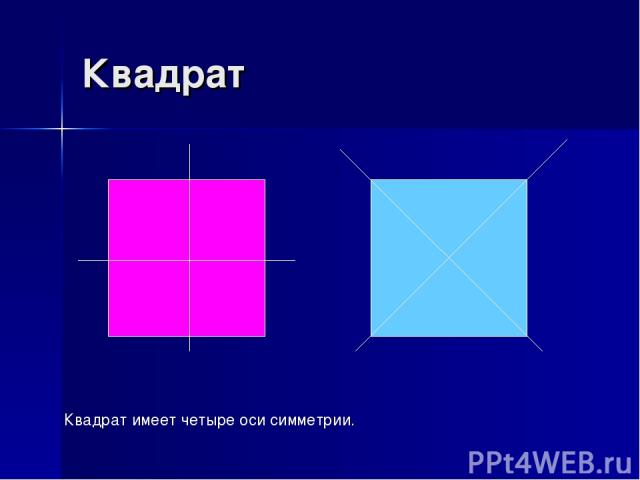
Квадрат Квадрат имеет четыре оси симметрии.

Круг Окружность имеет бесконечно много осей симметрии. Это любые прямые, проходящие через ее центр.

Правильный шестиугольник Как вы думаете, сколько осей симметрии имеет правильный шестиугольник?

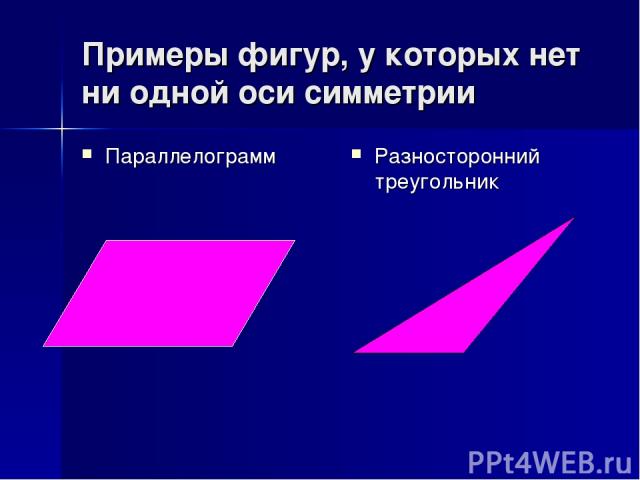
Примеры фигур, у которых нет ни одной оси симметрии Параллелограмм Разносторонний треугольник

Вывод: фигуры обладающие осевой симметрией: неразвернутый угол, равнобедренный и равносторонний треугольники, прямоугольник, ромб, квадрат, шестиугольник, круг, равнобедренная трапеция; круг обладает бесконечным числом осей симметрии; не обладают осевой симметрией параллелограмм и разносторонний треугольник.

Библиография: И.Ф.Шарыгин, Л.Н.Ерганжиева Наглядная геометрия. 5-6 классы Л.С.Атанасян и др. Геометрия 7-9 классы Л.С.Атанасян и др. Геометрия 10 - 11 классы