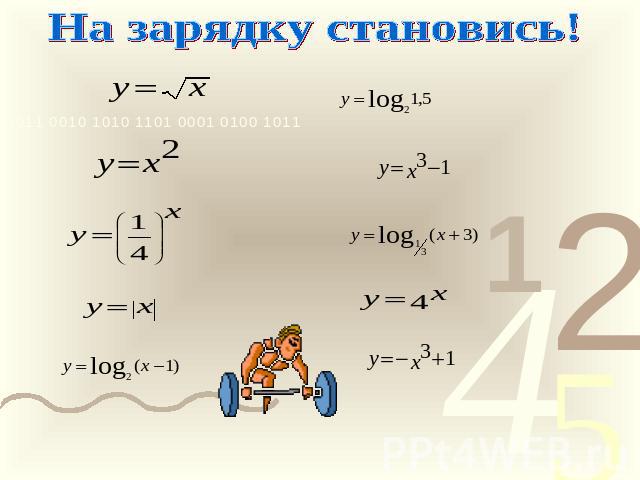Презентация на тему: Решение уравнений и неравенств

"Решение уравнений и неравенств"

Многообразие видов уравнений и методов их решений во всех частях КИМ показательные;логарифмические;тригонометрические;иррациональные;уравнения, содержащие неизвестную в основании и показателе степени;комбинированные;уравнения с параметрами.

Формулировки заданий укажите промежуток, которому принадлежит корень уравнения;найдите сумму ( произведение) корней уравнения;укажите количество корней уравнения;

Неравенства в КИМах дробно-рациональные;логарифмические;показательные;степенные;иррациональные;комбинированные, содержащие функции разных видов.

Формулировки заданий решите неравенство;укажите множество решений неравенств;вычислите сумму всех натуральных решений неравенства;найдите наименьшее (наибольшее) целое число, удовлетворяющее неравенству и т.д.

1. Укажите промежуток, содержащий корни уравнения. 2. Найдите сумму корней уравнения3. Сколько корней имеет уравнение?1. Решите неравенство2. Найдите сумму чисел, удовлетворяющих неравенству3. Найдите промежуток, содержащий наибольшее целое число, удовлетворяющее неравенству

Применение методов решения уравнений и неравенств

Способы решения систем уравнений

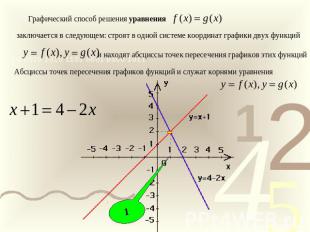
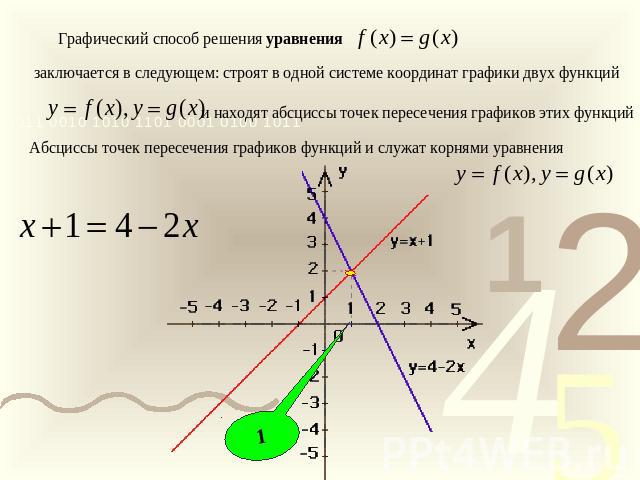
Графический способ решения уравнения заключается в следующем: строят в одной системе координат графики двух функцийи находят абсциссы точек пересечения графиков этих функцийАбсциссы точек пересечения графиков функций и служат корнями уравнения

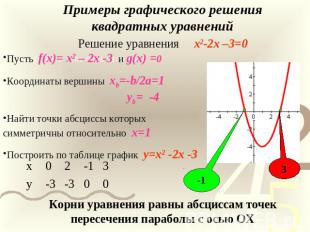
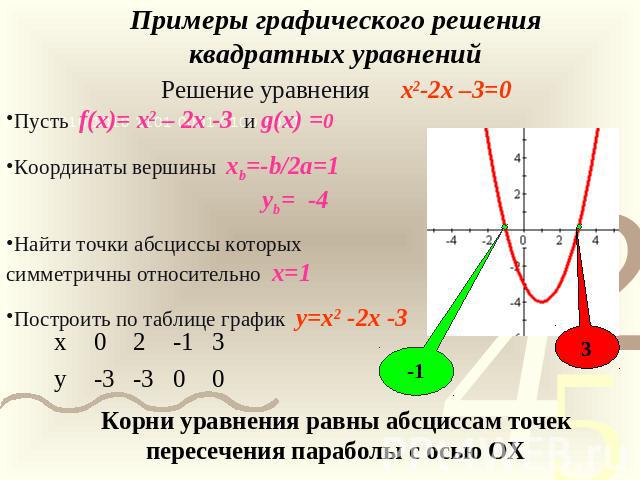
Примеры графического решения квадратныхРешение уравнения x2-2x –3=0 уравненийКорни уравнения равны абсциссам точек пересечения параболы с осью ОХ

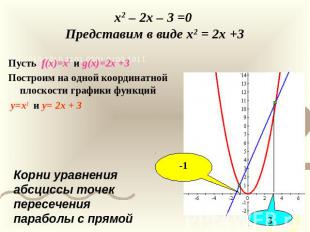
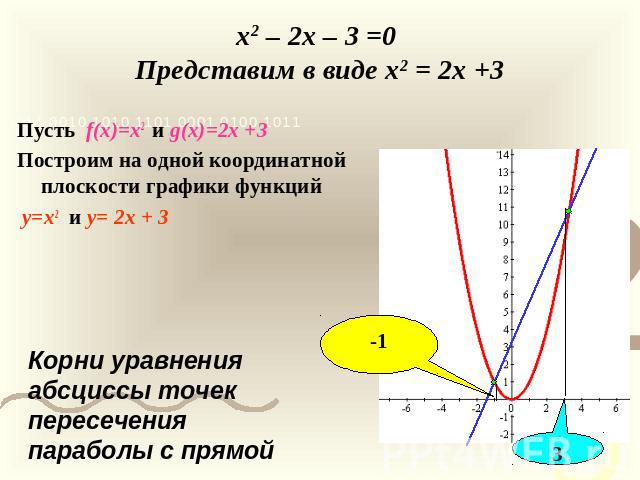
x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и g(x)=2x +3Построим на одной координатной плоскости графики функций y=x2 и y= 2x + 3Корни уравнения абсциссы точек пересечения параболы с прямой

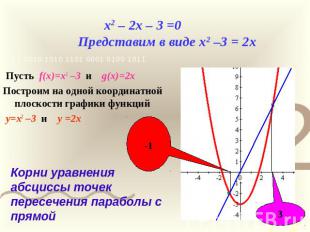
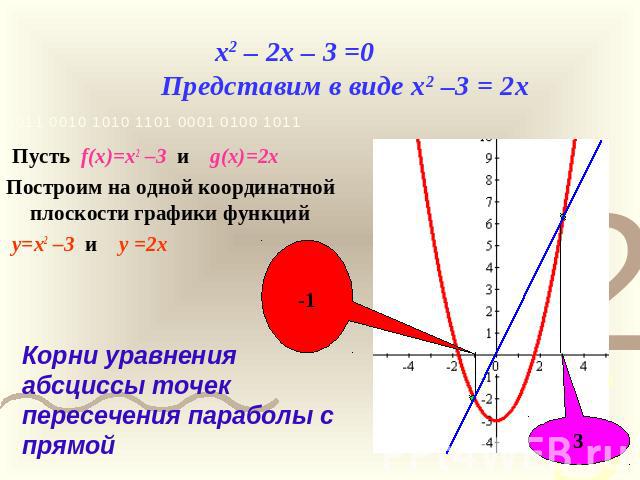
x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3 и g(x)=2xПостроим на одной координатной плоскости графики функций y=x2 –3 и y =2xКорни уравнения абсциссы точек пересечения параболы с прямой

"Графический способрешения уравнений и неравенств"

Графический метод решения некоторых уравнений весьма эффективен, когда нужно установить, сколько корней имеет уравнение.

Графический метод при определении количества корней уравнения

На зарядку становись!

Неравенства

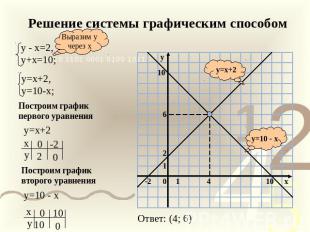
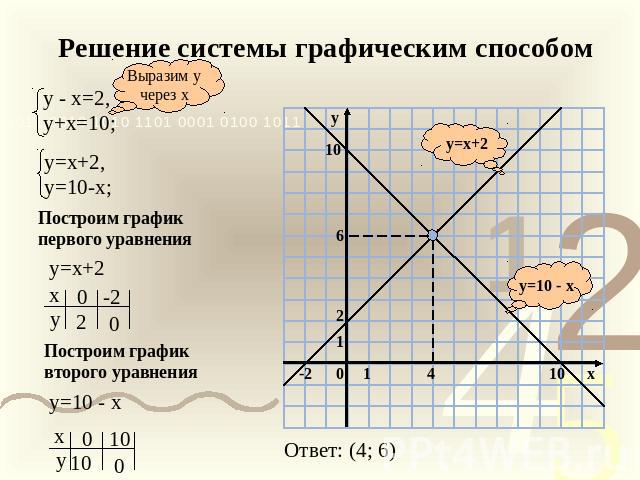
Решение системы графическим способом

Решение систем уравнений

ЕГЭ. Задания из части С.

Любви и взаимопонимания !