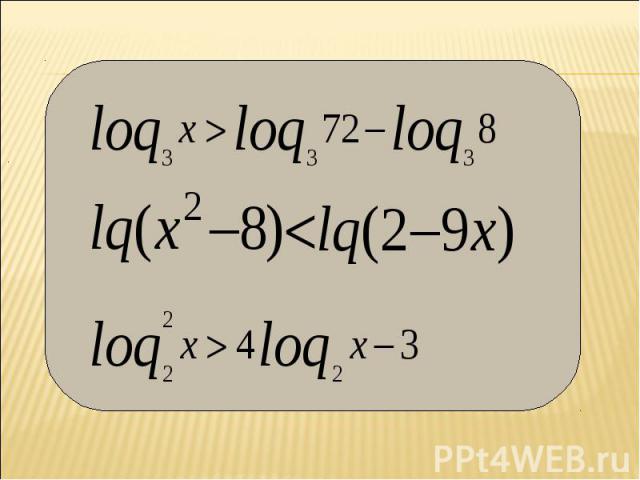Презентация на тему: Решение логарифмических уравнений и неравенств


Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими. Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.

Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах: Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:





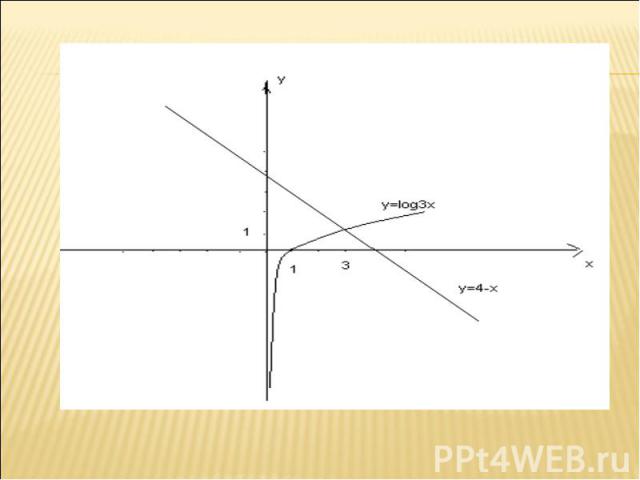
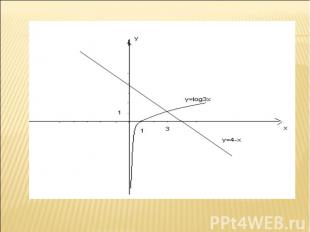
Найти корни уравнения Найти корни уравнения Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.

Решение неравенств, содержащих неизвестное под знаком логарифма, основано на следующих теоремах: Решение неравенств, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:

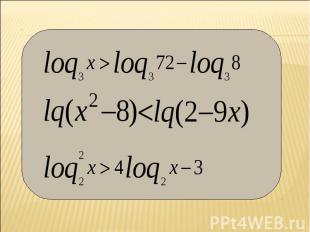

Комедия начинается с неравенства, Комедия начинается с неравенства, бесспорно правильного. Затем следует преобразование тоже не внушающее сомнения Большему числу соответствует больший логарифм, если функция возрастает, значит, После сокращения на Имеем 2>3. В чем ошибка этого доказательства?