Презентация на тему: Функция y = k√x . Подкоренная функция

Подкоренная функцияvk.com/sam_dok

Вспомним, что такое функция?Функция – это закон соответствия между множествами  X  и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества YПо другому, функция – это зависимость двух переменных X и Y

ОпределениеПодкоренная функция – это функция вида y = k√x , где y и x – зависимые переменные, а k – свободный коэффициент.

Область определения и область значения функции y = k√x Область определения D(y) –  это множество, на котором задаётся функция. D(y) - луч [0;+∞)Область значения E(y) -  множество значений, которые принимает функция в результате ее применения. E(y) – луч [0; +∞)*При условии, что k>0

Свойства функции y = k√x Свойство 1. y=0 при x=0; y>0 при x>0.Свойство 2. Функция возрастает на луче [0; +∞)Свойство 3. y наим = 0 (достигается при x=0), y наиб не существует.Свойство 4. y = k√x - непрерывная функция. *При условии, что k>0

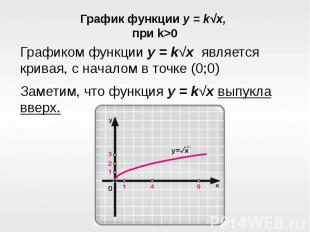
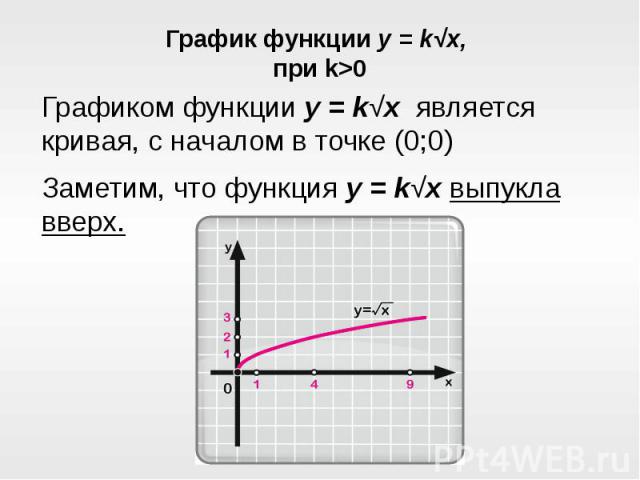
График функции y = k√x, при k>0Графиком функции y = k√x является кривая, с началом в точке (0;0)Заметим, что функция y = k√x выпукла вверх.

Рассмотрим график функции y = k√x, при k<0. Например y= -1√x. Чтобы построить график этой функции, создадим таблицу контрольных точек X и Y Рассмотрим график функции y = k√x, при k<0. Например y= -1√x. Чтобы построить график этой функции создадим таблицу контрольных точек X и Y Видим, что при k<0, переменная y стала принимать отрицательные значения, и график стал выпуклым вниз.

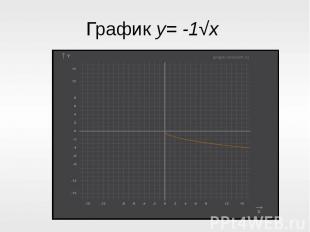
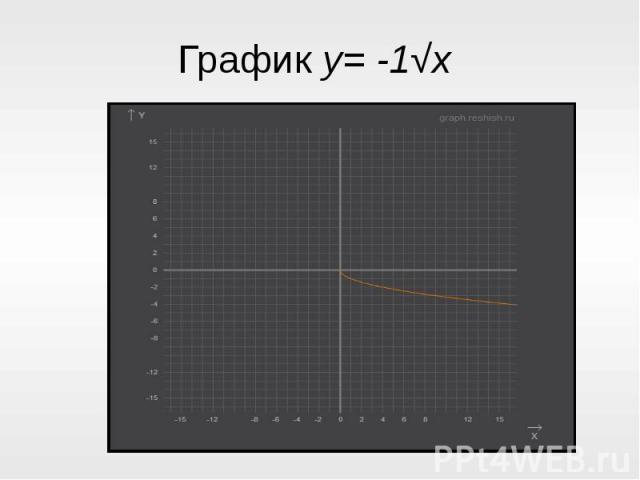
График y= -1√x

Сделаем выводыПри k<0, функция y = k√x обладает следующими свойствами:1. у = 0 при х = 0; у < 0 при х > 0.2. Функция убывает на луче [0; +∞]. 3. унаиб= 0 (достигается при х = 0), унаим не существует.4. Функция непрерывна на луче [0; +∞] 5. E(y)- луч (-∞;0)

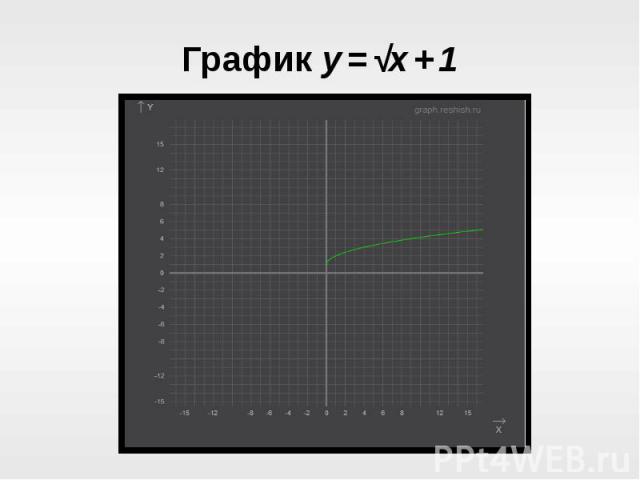
Рассмотрим график функции y = √x + m,Рассмотрим график функции y = √x + m,где m = 1.Создадим опорную таблицу:Строим график (см. 11 слайд)Видим, что график имеет начало в точке (0;1). Следовательно, коэффициент m показывает, насколько ед. отрезков вверх(или вниз) график функции y = √x сдвинется по оси Oy .

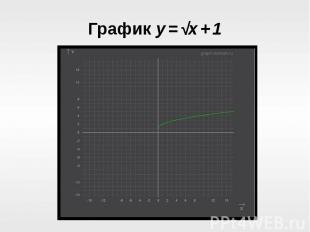
График y = √x + 1

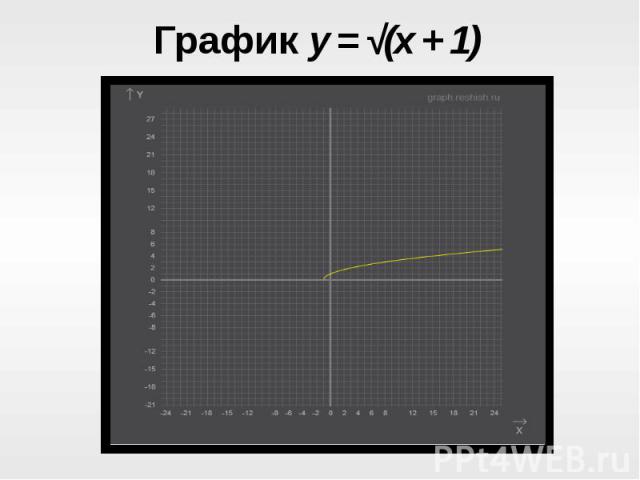
Рассмотрим график функции y = √(x + n), где Рассмотрим график функции y = √(x + n), где n=1.Создадим опорную таблицу:Видим, что график имеет начало в точке (-1;0)Следовательно, коэффициент n показывает, насколько ед. отрезков влево(или вправо) график функции y= √ x сместится по оси OxЗаметим , если n>0, график смещается влево; если n<0, график смещается вправо.

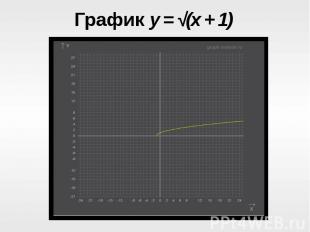
График y = √(x + 1)

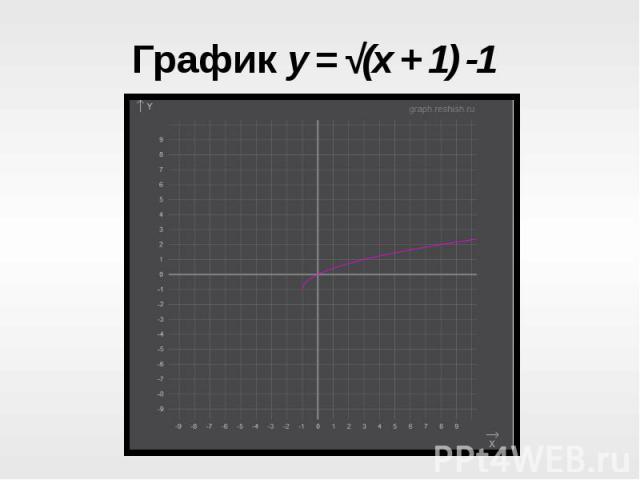
Рассмотрим график функции y = √(x + n) + m,Рассмотрим график функции y = √(x + n) + m,где n=1 , m=-1Создадим опорную таблицу :Видим, что график имеет начало в точке:(-1;-1).Следовательно, коэффициенты n и m показывают, как сместился график y= √ x , одновременно по осям Ox и Oy соответственно.

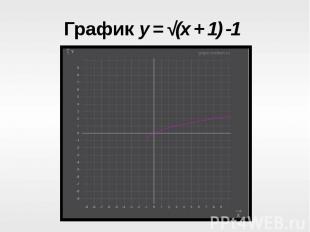
График y = √(x + 1) -1

Построить график функцииПостроить график функции y = √(x + n) + m , можно не только по опорной таблице , но и по контрольным точкам , сместив координатную прямую по осям Ox и Oy.Так, например, график функции y = √(x + 2) -3 можно построить сместив ось Ox на 2 ед. отрезка вверх по оси Oy, а ось Oy сместив на 3 ед . отрезков вправо по оси Ox. После чего, в новой системе координат построить график y√x по контрольным точкам.