Презентация на тему: Логарифмическая функция

Логарифмическая функция

Решим уравнение относительно х: Теперь поменяем ролями аргумент и функцию(соответственно изменим и обозначения)

В математике и ее приложениях часто встречается логарифмическая функция y=logax где а - заданное число, а>0, а ≠ 1.

Как называется функция, обратная показательной? Логарифмическую функцию можно получить путем обращения ___________ функции. Напишите функцию обратную функции Какая функция является обратной для функции Функция, обратная показательной, называется логарифмической. Показательной.

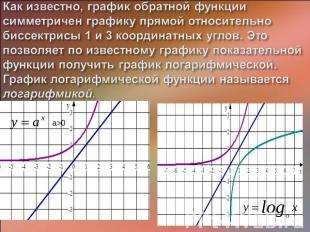
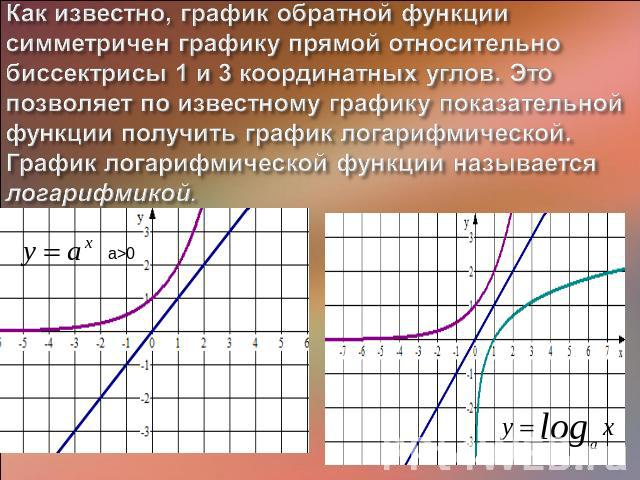
Как известно, график обратной функции симметричен графику прямой относительно биссектрисы 1 и 3 координатных углов. Это позволяет по известному графику показательной функции получить график логарифмической. График логарифмической функции называется логарифмикой.

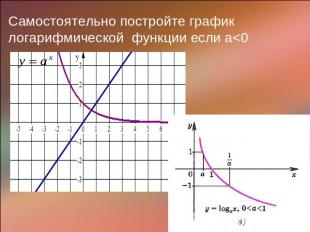
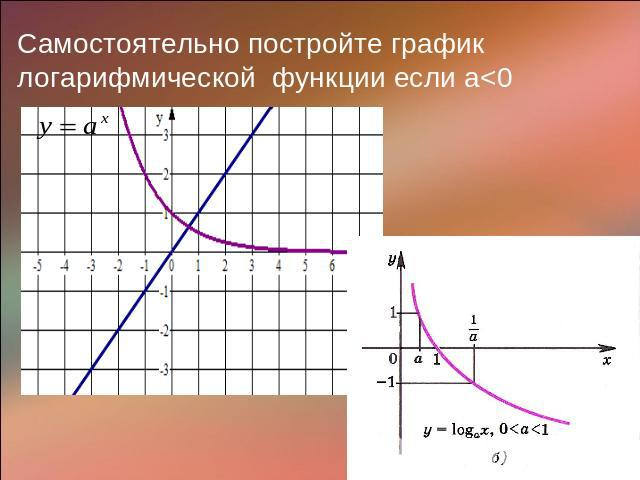
Самостоятельно постройте график логарифмической функции если а<0

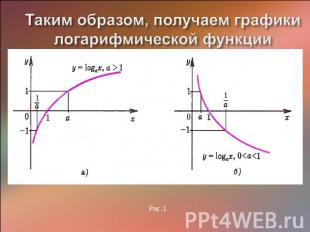
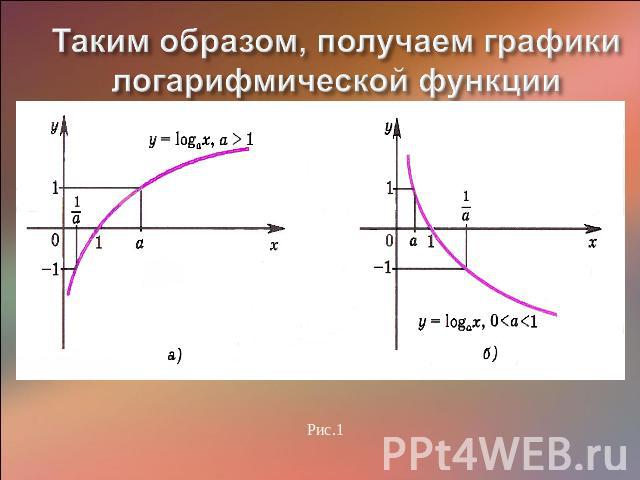
Таким образом, получаем графики логарифмической функции

Свойства логарифмической функции 1) Область определения логарифмической функции - множество всех положительных чисел R+. 2) Множество значений логарифмической функции - множество R всех действительных чисел. 3) Логарифмическая функция y=logax является возрастающей на промежутке х> 0, если а> 1 (рис. 1а), и убывающей, если О < а < 1 (рис. 1б). 4) Если а> 1, то функция y=logax принимает положительные значения при х> 1, отрицательные при 0<х< 1. Если 0<а< 1, то функция y=logax принимает положительные значения при 0<х<1, отрицательные при х>1.