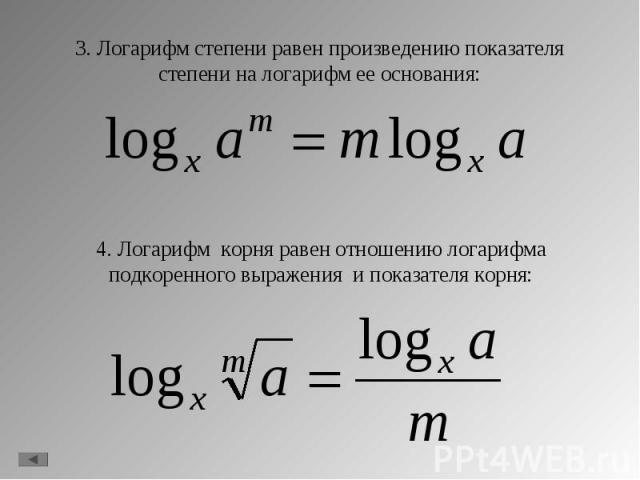Презентация на тему: Логарифмическая функция

1. Понятие логарифма. 1. Понятие логарифма. 2. Графики логарифмических функций. 3. Свойства логарифмов. 4. Решение логарифмических уравнений. 5. Решение логарифмический неравенств.

Если основанием является 10, то вместо log10 x пишут lg x. Если основанием является 10, то вместо log10 x пишут lg x. Для введения следующего определения стоит понимать что за число e. Число е есть предел, к которому стремится при неограниченном возрастании n. Т.е Вместо loge x принято писать ln x.

Из определения логарифма следует следующее тождество: Из определения логарифма следует следующее тождество:

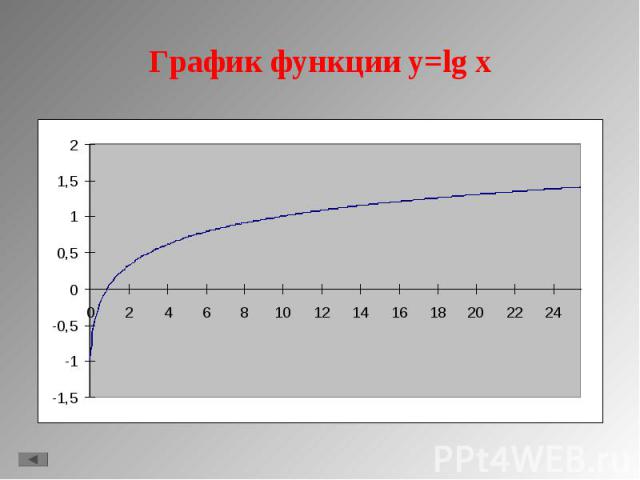
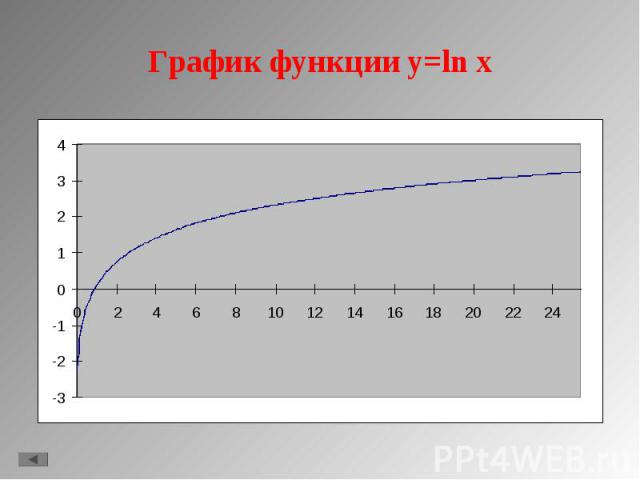
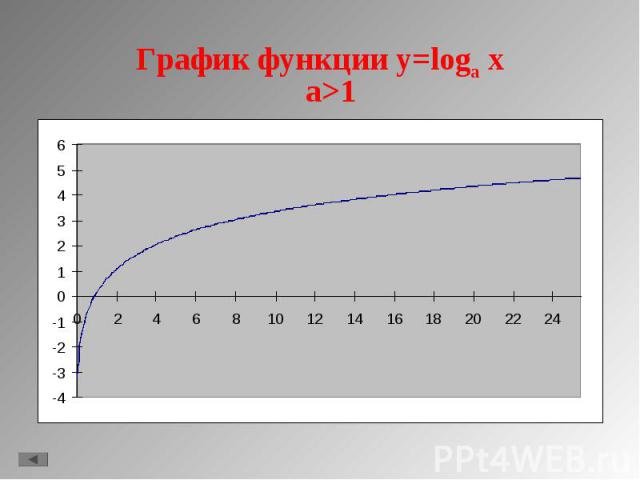
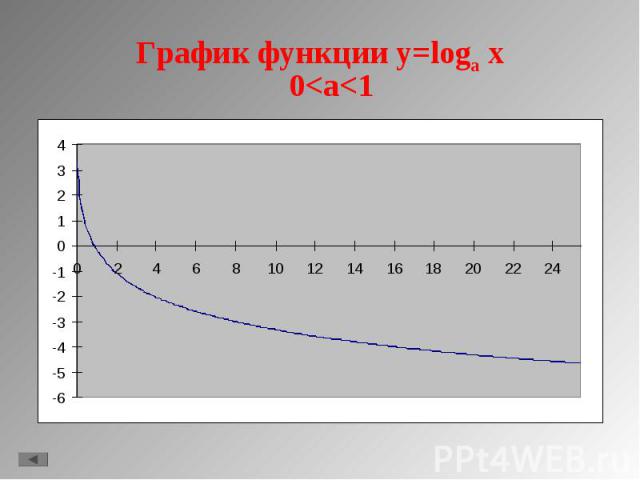
1. y = lg x 1. y = lg x 2. y = ln x 3. y = loga x, a>1 4. y = loga x, 0<a<1 5. Свойства функции.

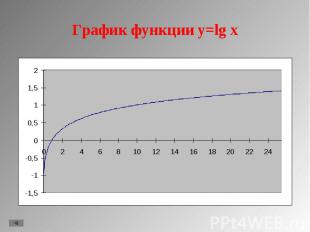
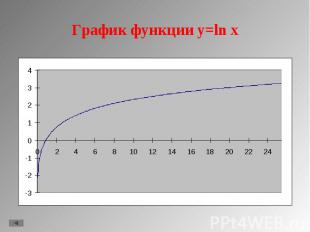
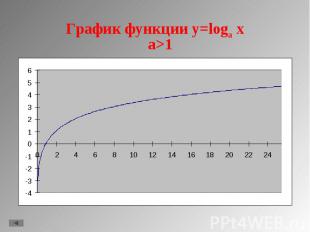
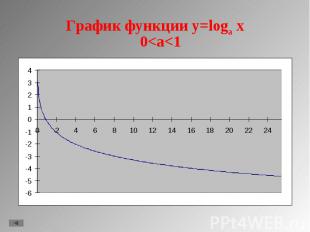
D(f)=(0;+∞); D(f)=(0;+∞); Не является ни четной, ни нечетной; При a>1 функция возрастающая, при 0<a<1 функция убывающая; Не ограничена; Не имеет ни максимального, ни минимального значения; Непрерывна; E(f)=(- ∞;+ ∞); Асимптота х=0; Выпукла вверх при a>1, выпукла вниз при 0<a<1 Стоит заметить, что график проходит через точки (1;0) и (а;1)

1. Логарифм произведения. 1. Логарифм произведения. 2. Логарифм частного. 3. Логарифм степени. 4. Логарифм корня. 5. Переход от одного показателя к другому. 6. Свойства натуральных логарифмов.

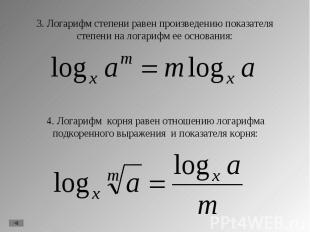
Над презентацией работали: Над презентацией работали: Киселев Михаил Таячков Максим Кирилов Дмитрий